Table of Contents
Explain in Detail :Properties of Tangent of a Circle
The tangent of a circle is a line that intersects a circle at a single point and is perpendicular to the radius at that point. The tangent line is also the shortest distance from the point of intersection to the circle.

Tangent to a circle is the line that touches the circle at only one point. There can be only one tangent at a point to circle. Point of tangency is the point at which tangent meets the circle. Now, let’s prove tangent and radius of a circle are perpendicular to each other at the point of contact.
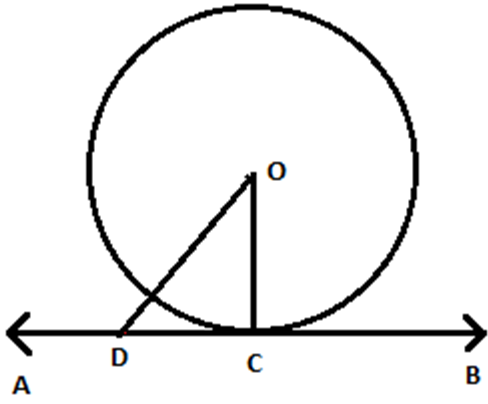
Consider a circle in the above figure whose centre is O. AB is the tangent to a circle through point C.
Take a point D on tangent AB other than C and join OD. Point D should lie outside the circle because; if point D lies inside, then AB will be a secant to the circle and it will not be a tangent.
Therefore, OD will be greater than the radius of circle OC. This happens for every point on AB except the point of contact C.
It can be concluded that OC is the shortest distance between the centre of circle O and tangent AB.
Since, the shortest distance between a point and a line is the perpendicular distance between them,
OC is perpendicular to AB.
From the above discussion, it can be concluded that:
- The tangent touches the circle at only one point
- We can call the line containing the radius through the point of contact as ‘normal’ to the circle at the point
Note: The tangent to a circle is a special case of the secant when the two endpoints of its corresponding chord coincide.
Tangent to a circle is the line that touches the circle at only one point. There can be only one tangent at a point to circle. Point of tangency is the point at which tangent meets the circle. Now, let’s prove tangent and radius of a circle are perpendicular to each other at the point of contact.

Consider a circle in the above figure whose centre is O. AB is the tangent to a circle through point C.
Take a point D on tangent AB other than C and join OD. Point D should lie outside the circle because; if point D lies inside, then AB will be a secant to the circle and it will not be a tangent.
Therefore, OD will be greater than the radius of circle OC. This happens for every point on AB except the point of contact C.
It can be concluded that OC is the shortest distance between the centre of circle O and tangent AB.
Since, the shortest distance between a point and a line is the perpendicular distance between them,
OC is perpendicular to AB.
From the above discussion, it can be concluded that:
- The tangent touches the circle at only one point
- We can call the line containing the radius through the point of contact as ‘normal’ to the circle at the point
Note: The tangent to a circle is a special case of the secant when the two endpoints of its corresponding chord coincide.
The Formula of Tangent of a Circle
The tangent of a circle is the length of the line segment that is perpendicular to the circle at the point of tangency.





