Table of Contents
Introduction to Value of sin 15
The sine of 15 degrees, abbreviated sin 15°, is a trigonometric function that expresses the ratio of the length of a right triangle’s side opposite a 15-degree angle to the length of the hypotenuse. It is an irrational number that is roughly equivalent to 0.2588.
The Value of Sin 15°
To get the value of Sin 15°, consider the formula for compound angles.
Sin(A – B) = sinA cosB – cosA sinB
Substitute the values A = 45°, B = 30°
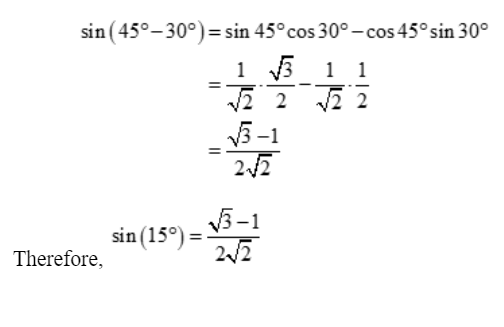
The Value of Sin 15° in decimal value:
The value Sin 15° of in the decimal values:
We know that
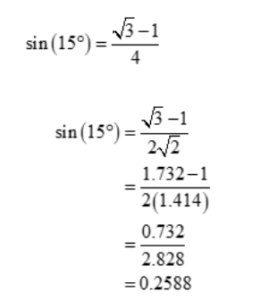
Therefore, the decimal value of Sin 15° is 0.2588
The value of cos 15
To get the value of Cos 15° degrees, consider the formula for compound angles.
Cos(A – B) = cosA cosB – sinA sinB
Substitute the values A = 45°, B = 30°
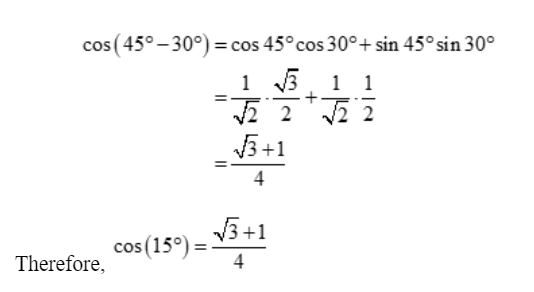
Problems involving sin 15
Problem No. 1: Find the value of sin 15° + sin 30° .cos 15°
Solution: The given expression is sin 15° + sin 30° .cos 15°
Plug in the values
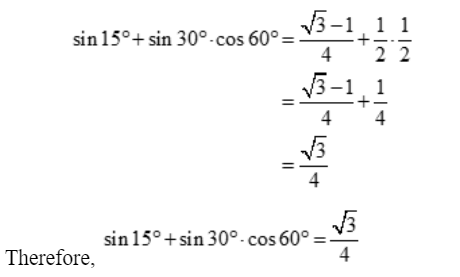
Problem No. 2: Find the value of Sin 15° – Cos 15°
Solution: The given expression is Sin 15° – Cos 15°
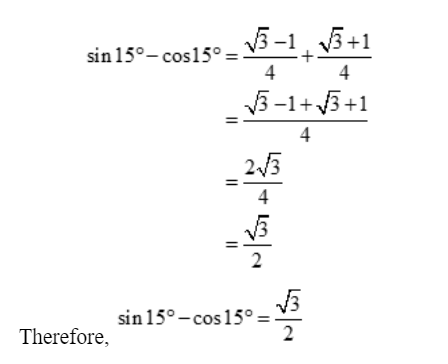
Frequently asked questions about sin 15 degrees
What is the value of the sin 15?
opposite to the angle to the length of the hypotenuse in a right triangle. To find the sine of 15 degrees, we can draw a right triangle with one of the angles as 15 degrees. Using basic trigonometric ratios, sine theta = opposite side/hypotenuse. For a 15 degree angle, the opposite side will be 0.2588 and hypotenuse will be 1. So, sin 15 = 0.2588.
What is the value of 15 in trigonometry?
15 degrees represents an acute angle measuring one-twenty-fourth of a full circle rotation. One full rotation is 360 degrees, so 15 degrees would be 360/24 = 15 degrees. 15 degrees is a common angle used in trigonometry problems involving 30-60-90 degree special right triangles. Knowing the trig values of 15 degrees is useful for solving many problems.
What is value of cos 15?
cosine of an angle is the ratio of the length of the side adjacent to the angle to the length of the hypotenuse. Using a 15 degree right triangle with hypotenuse 1 and opposite side 0.2588, we can determine the adjacent side using Pythagorean theorem. Adjacent side = sqrt(1^2 - 0.2588^2) = 0.9659. Therefore, cos 15 = adjacent/hypotenuse = 0.9659.
How do you find sin 15 without a calculator?
sin 15 without calculator, you can construct a 30-60-90 degree special right triangle, which contains an angle of 30 degrees and another of 60 degrees. The hypotenuse is always twice the length of the shorter side. For a hypotenuse of 2, the shorter side is 1. Sin 30 = Opposite/Hypotenuse = 1/2 = 0.5. Sin 15 is half of sin 30, so sin 15 = 0.5/2 = 0.2588.
What is cos 15 degrees in terms of sine?
We know that the sine, cosine and tangent of an angle have certain relationships. Since sum of angles of a triangle is 180 degrees, cos 15 = sin (180 - 15) = sin 165. 165 can be simplified to 75 (360 - 165). Therefore, cos 15 degrees = sin 75 degrees.
What is the value of sin 18?
sin 18, we can use a calculator which gives 0.3090. Or construct a 36-54-90 triangle with hypotenuse 2. Here, shorter side = 1, so sin 36 = Opposite/Hypotenuse = 1/2 = 0.5. Sin 18 is half of sin 36, so sin 18 = 0.5/2 = 0.3090.









