Table of Contents
Area of Isosceles Triangle
An isosceles triangle is a type of triangle that has two sides of equal length and two equal angles opposite those sides. The area of an isosceles triangle is a fundamental concept in geometry and can be determined using various methods.
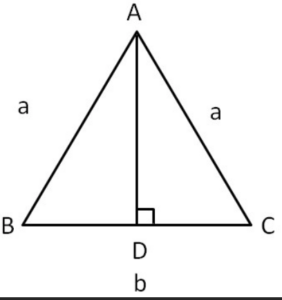
Area of the triangle
The most common way to calculate the area of an isosceles triangle is by utilizing the base and height of the triangle. The base refers to the length of the unequal side, while the height represents the perpendicular distance from the base to the opposite vertex or the midpoint of the base.
The formula to find the area of an isosceles triangle using the base and height is:

Heron’s Formula
In this formula, the base and height are multiplied by half to obtain the area. It is important to ensure that the height is measured perpendicularly to the base for accurate calculations.
If the lengths of all three sides of the isosceles triangle are known, Heron’s formula can be used to calculate the area. Heron’s formula is a general formula for calculating the area of any triangle using the lengths of its sides.
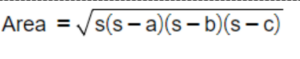
Where, s is the semi perimeter of the triangle and a, b and c are lengths of sides of a triangle.
Substituting the lengths of an isosceles triangle, we get,
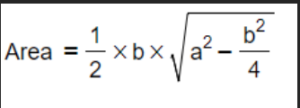
It is important to note that the area of an isosceles triangle is always non-negative and is expressed in square units, such as square centimetres (cm²) or square inches (in²).
Solved Examples on the Area of Isosceles Triangle
Example 1. In an isosceles triangle, the lengths of the two equal sides are both 5 inches, and the height is 4 inches. Find its area.
Solution:
Using the formula for the area of an isosceles triangle:
Area = (1/2) x side length x height
Area = (1/2) x 5 inches x 4 inches
Area = 10 square inches
Therefore, the area of the isosceles triangle is 10 square inches.
Example 2. Given an isosceles triangle with a base of length 8 cm and a height of 6 cm. Find its area.
Solution:
Using the formula for the area of an isosceles triangle:
Area = (1/2) x base x height
Area = (1/2) x 8 cm x 6 cm
Area = 24 square cm
Therefore, the area of the isosceles triangle is 24 square cm.
Example 3. An isosceles triangle has side lengths of 7 cm, 7 cm, and 10 cm. Calculate its area.
Solution:
Using Heron’s formula to find the area of the isosceles triangle:
Semi-perimeter, s = (7 cm + 7 cm + 10 cm) / 2 = 12 cm
Area = √(s x (s – a) x (s – b) x (s – c))
Area = √(12 cm x (12 cm – 7 cm) x (12 cm – 7 cm) x (12 cm – 10 cm))
Area = √(12 cm x 5 cm x 5 cm x 2 cm)
Area = √600 square cm ≈ 24.49 square cm
Therefore, the area of the isosceles triangle is approximately 24.49 square cm.
Frequently Asked Questions on Area of Isosceles Triangle
How do you find the height and area of an isosceles triangle?
To find the height, divide the triangle into two right triangles by drawing a perpendicular line from the base to the top vertex. Use the Pythagorean theorem to find the height. For the area, use the formula: Area = (base × height) / 2.
What is the formula of area of an isosceles triangle?
The formula is: Area = (base × height) / 2.
What is the area of the right angle triangle and isosceles triangle?
For a right angle triangle: Area = (base × height) / 2. For an isosceles triangle: Area = (base × height) / 2.
What is the area of the isosceles triangle Class 9?
The formula to find the area remains the same: Area = (base × height) / 2.
What is the area to find isosceles triangle?
You can find the area of an isosceles triangle using the formula: Area = (base × height) / 2.
What is the formula for the isosceles right triangle?
For an isosceles right triangle, the formula for the area is: Area = (leg × leg) / 2, as both legs are equal in length.
What is the area of an isosceles triangle with sides?
If you know the length of the sides, you can find the base and height using the Pythagorean theorem, then apply the formula: Area = (base × height) / 2.
How to find the area of an isosceles triangle without height?
If you know the lengths of all three sides, you can use Heron's Formula to find the area. First find the semi-perimeter (s) using the formula s = (a + b + c) / 2, where a, b, and c are the lengths of the sides. Then the area is given by: Area = √{s(s - a)(s - b)(s - c)}.







