Table of Contents
Introduction to Derivative of tan(x)
In calculus, the derivative of tan(x) is a fundamental idea. The tangent function, or tan(x), is a relation between the sine and cosine of an angle. For the purpose of solving problems involving rates of change and optimisation, understanding its derivative is essential. This article examines the formula for calculating the derivative of tan(x), several differentiation techniques, and common issues with solutions.
Formula for the derivative of tan(x)
The following formula can be used to represent the derivative of tan(x):
d/dx(tan x) = sec2x
Here sec2x represents the square of secant x.
Derivative of Tan(x) using first principle of differentiation
We can start with the definition of the derivative to determine the derivative of tan(x) using the first principle of differentiation:
The first principle of differentiation states that,
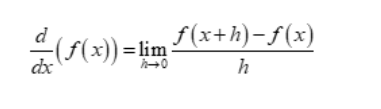
Substitute f(x) = tan x
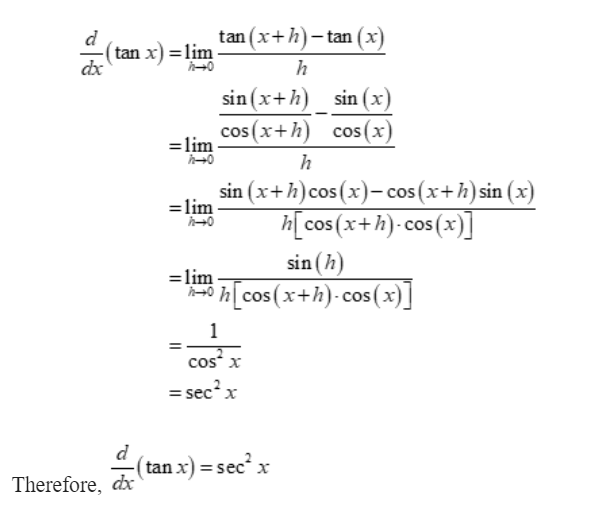
Derivative of Tan(x) using Chain rule
As an alternative, the chain rule can be used to determine the derivative of tan(x). We may split them out and use the chain rule by thinking of tan(x) as the combination of two functions, u(x) = tan(x) and v(x) = x:
d/dx (tan x) = d/dx (tan x)d/dx(x)
= sec2x . 1
= sec2x
Therefore, d/dx(tan x) = = sec2x
Also Check For:
Conclusion
Finally, the formula d/dx(tan x) = sec2x is used to determine the derivative of tan(x). It can be obtained by applying various techniques, including the quotient rule, chain rule, and first principle of differentiation. It is crucial to comprehend the derivative of tan(x) for a number of calculus applications and mathematical analytical tasks.
Derivative of Tan(x) using Quotient Rule
Applying the quotient rule is another way to determine the derivative of tan(x). We may use the quotient rule to separate the numerator and denominator of tan(x) by expressing it as sin(x)/cos(x):
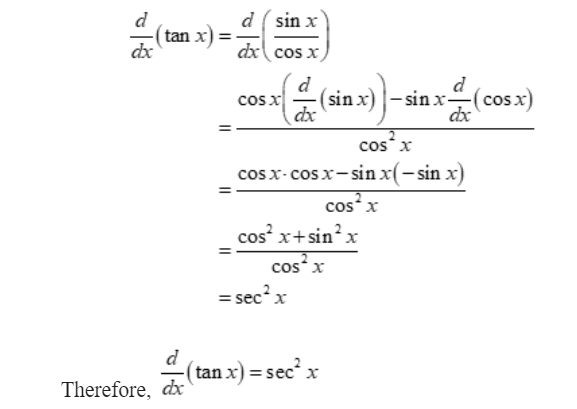
Problems related to the derivative of Tan(x)
Find the derivative of the expression f(x) = 2tan(x) – sin(x).
Solution: Use the derivative formulas for tan(x) and sin(x) to separately differentiate each term. f'(x) = 2sec2x – cos x
Calculate the tangent line’s equation at the point (π/4, 1)on the curve y = tan(x).
Solution: Use the derivative formula to determine the derivative of tan(x). The derivative is 2 at x = π/4.
Thus, y – 1 = 2(x – π/4)is the equation for the tangent line.
Frequently asked questions on Derivative of Tan(x)
What is the second derivative of tanx?
The derivative of tan t is sec^2 t because using the quotient rule, the derivative of tan t = sin t/cos t is (cos t * cos t - sin t * -sin t) / (cos^2 t) which simplifies to sec^2 t.
What is the second derivative of tanx?
The second derivative of tanx is 2sec^2x tanx. To find this, take the derivative of sec^2x (the first derivative of tanx) using the chain rule. The derivative of sec^2x is 2secx tanx.
What is derivative tan 2x?
The derivative of tan 2x is 2sec^2 2x. Using the chain rule, the derivative of tan 2x is 2(sec^2 2x) which is 2sec^2 2x.
What is the derivative of tan 1x?
The derivative of tan 1x is sec^2 1x. This uses the same logic as the derivative of tan t.
What is the derivative of sin and cos?
The derivative of sin is cos because sin is one of the elementary trigonometric functions whose derivative is defined as cos. The derivative of cos is -sin, using the same logic that cos is an elementary trigonometric function whose derivative is defined as -sin.









