Table of Contents
Introduction to Harmonic Mean
The harmonic mean is a mathematical concept that is used to compute the average value of a group of numbers, especially when working with rates, ratios, or reciprocals. It gives smaller numbers greater weight, making it appropriate for circumstances when their influence is critical. It is used in a variety of disciplines, including banking and engineering.
Definition of Harmonic Mean
The harmonic mean is a mathematical average that is determined by taking the reciprocal of each integer in a set, computing the arithmetic mean of those reciprocals, and then taking the reciprocal of the result.
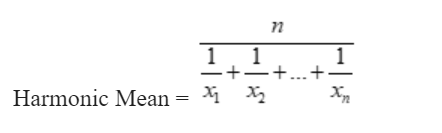
where n represents the total number of values in the set and x1, x2, x3,…, xn represent the individual values. When working with rates, ratios, or numbers containing reciprocals, the harmonic mean is especially useful..
What are the steps to find the Harmonic Mean?
Follow these procedures to get the harmonic mean of a set of numbers:
-
- Determine the collection of numbers for which you wish to calculate the harmonic mean.
- Take the inverse of every integer in the set. To achieve this, divide 1 by each integer in the set.
- Add the reciprocals acquired in step 2 to get the total.
- Determine how many values are in the set.
- Divide the total number of values by the sum of the reciprocals acquired in step 3.
- The harmonic mean has the following mathematical formula:
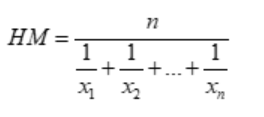
Where n is the total number of values and x1, x2, x3, …, xnare the individual numbers in the set. - You may get the harmonic mean of a given collection of integers by following these steps and applying the formula.
The properties of the Harmonic Mean
- Extreme value sensitivity: The harmonic mean is extremely sensitive to extreme values in a data collection. A single large or small number can have a big influence on the harmonic mean.
- Weighting smaller values: The harmonic mean weights smaller values in the data set more heavily. When the emphasis is on the smaller values and their contribution to the average, this is an acceptable metric.
- Inequality with arithmetic mean: In general, the harmonic mean of the same set of values is always smaller than or equal to the arithmetic mean. Equality exists only when all values are the same.
- Limitation due to zero values: If any value in the data set is 0, the harmonic mean is always zero.
- Relationship: The harmonic mean is the reciprocal of the arithmetic mean of the values’ reciprocals. Because of the reciprocal connection, it is appropriate for situations requiring rates, ratios, or numbers stated as reciprocals.
- The harmonic mean is not transitive, which means that the harmonic mean of a collection of values is not always equal to the harmonic mean of a subset of those values.
- Averaging rates: The harmonic mean is frequently used to compute average rates, such as average speed or average growth rates.
- Understanding these qualities aids in the interpretation of the harmonic mean and its use in specific circumstances including rates, ratios, and reciprocals.
Problems on Harmonic Mean
Problem 1: Calculating Average Speed
A automobile goes at 60 km/h in the first half of the voyage and 80 km/h in the second. Using the harmonic mean, compute the average speed for the whole voyage.
Solution: To compute the average speed using the harmonic mean, we first take the reciprocal of each speed, then the arithmetic mean of those reciprocals, and finally the reciprocal of the resultant number.
1/60 and 1/80 reciprocal
Reciprocal arithmetic mean =
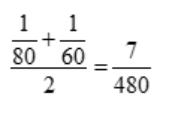
Arithmetic mean reciprocal = 480/7
As a result, the overall average speed is 68.57 km/h
Problem 2: Calculating Efficiency
A machine is 80% efficient for one task and 60% efficient for another. Using the harmonic mean, compute the total efficiency.
Solution: To compute the total efficiency using the harmonic mean, we first take the reciprocal of each efficiency, then the arithmetic mean of those reciprocals, and finally the reciprocal of the resultant value.
1/80 and 1/60 reciprocal
Reciprocal arithmetic mean: (1/80 + 1/60) / 2 = 7/240
Arithmetic mean reciprocal: 1 / (7/240) = 240/7
As a result, the overall efficiency is around 34.29%.
These questions demonstrate how the harmonic mean may be used to calculate average speed and overall efficiency, as well as its application in rate, ratio, and reciprocal scenarios.
Frequently asked questions on Harmonic Mean
What is the meaning of harmonic mean?
The harmonic mean is a mathematical concept that is used to calculate the average of a set of numbers. It is specifically designed to deal with situations where the numbers involved have a reciprocal relationship. The harmonic mean is the reciprocal of the arithmetic mean of the reciprocals of the numbers in the set.
What is the harmonic mean of 3 and 5?
To find the harmonic mean of two numbers, such as 3 and 5, we first take the reciprocals of the numbers (1/3 and 1/5), then calculate their arithmetic mean (average) which is (1/3 + 1/5)/2 = 8/15. Finally, we take the reciprocal of the arithmetic mean, which gives us the harmonic mean. In this case, the harmonic mean of 3 and 5 is 15/8.
What is harmonic mean and its formula?
The harmonic mean is a type of average that is used when dealing with numbers that have a reciprocal relationship. The formula for the harmonic mean is: Harmonic Mean = n / (1/x₁ + 1/x₂ + ... + 1/xₙ) Where n is the total number of values and x₁, x₂, ..., xₙ are the individual values.
What is harmonic mean and series?
In mathematics, a harmonic series is an infinite series that consists of the reciprocals of positive integers. It is denoted by Hₙ, where n represents the term number. The harmonic mean is closely related to the concept of a harmonic series, but they are not the same thing. The harmonic mean is used to calculate the average of a set of numbers, while the harmonic series is an infinite sum.
What is harmonic mean in statistics?
In statistics, the harmonic mean is a measure of central tendency that is used to find the average of a set of values. It is particularly useful when dealing with rates, ratios, or other situations where the reciprocals of the values are of interest. The harmonic mean is defined as the reciprocal of the arithmetic mean of the reciprocals of the values in the set. It is often used to calculate average rates or averages of rates.








