Table of Contents
Introduction to Integration
Integration is a fundamental concept in calculus that deals with finding the antiderivative of a function. It involves calculating the accumulated change of a quantity over an interval. Integration allows us to determine areas under curves, volumes of solids, and solve diverse mathematical problems. It plays a vital role in various fields, including physics, engineering, economics, and is essential for advanced mathematical analysis..
Definition of integration
In calculus, integration is defined as the process of determining a function’s antiderivative. Integration is the inverse process of differentiation, and it includes determining the entire area under a curve or the accumulated change. The outcome of integration is a family of functions, each of which differs by a constant known as the constant of integration. Integration is essential in calculus since it allows for the computation of areas and volumes as well as the solution of a wide range of mathematical problems in numerous domains.
Integration In math
Integration is a fundamental subject in calculus that deals with determining a function’s antiderivative. It entails computing the total area or cumulative change under a curve. Integration is the inverse of differentiation in that the derivative of a function tells its rate of change, whereas the integral gives the original function when the rate of change is known.
Integration is important in many domains of mathematics, science, engineering, and economics. It is used to compute areas, volumes, work, probability, and to answer a variety of mathematical issues that include continuous values. Integration is a strong technique for analysing function behaviour and comprehending the cumulative impacts of change..
Integral calculus
Integral calculus is a branch of calculus that deals with computing areas under curves and determining the antiderivative of functions. It focuses on integration, which is the opposite of difference. Understanding cumulative amounts, volumes, effort, and numerous mathematical applications in science, engineering, and economics is impossible without integral calculus..
Integration – Reverse process of differentiation
- Because integration is the inverse process of differentiation, we may discover the original function from which it was formed if we have the derivative.
- Consider differentiation as determining the rate of change or slope of a function at any point. In contrast, integration operates in the other direction. It collects information about the rate of change and discovers the original function that caused it.
- When we differentiate a function, we lose some information about the function’s constant term. Integration replaces the missing information with an arbitrary constant known as the constant of integration.
- If we differentiate the function f(x) = x2, for example, we obtain its derivative f'(x) = 2x. When we integrate 2x, we get the original function f(x) = x2, but we also need to add a constant C because we lost information about the constant term when differentiating.
In summary, differentiation determines a function’s rate of change, whereas integration goes backward to get the original function from its rate of change. Differentiation and integration are essential procedures in calculus that allow us to understand function behaviour and solve a variety of mathematical issues.
Indefinite integral
Indefinite integrals, a concept in integral calculus, entail determining antiderivatives of functions that do not have particular integration limits. They provide a family of functions that differ by an arbitrary constant called the constant of integration. Indefinite integrals, denoted by the symbol, allow us to discover general solutions to differential equations and are an important tool for computing accumulated quantities and understanding the behaviour of functions..
Definite integral
In integral calculus, definite integrals require computing the cumulative area between a function’s curve and the x-axis over a certain interval. In contrast to indefinite integrals, definite integrals have upper and lower integration limits represented by “a” and “b,” respectively. The outcome of a definite integral is a single numerical number that reflects the net area encompassed by the curve. Definite integrals are used in mathematics, physics, and engineering to obtain total amounts, average values, and address numerous real-world situations..
Integral formulae for algebraic functions
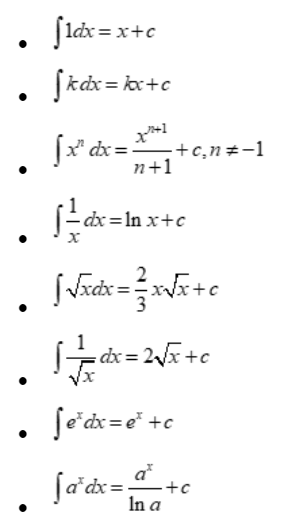
Rules for integration
Here are some common integration formulas for algebraic functions:
Power Rule:
∫ x^n dx = (x^(n+1))/(n+1) + C, where n ≠ -1.
Constant Multiple Rule:
∫ k * f(x) dx = k * ∫ f(x) dx, where k is a constant.
Sum/Difference Rule:
∫ [f(x) + g(x)] dx = ∫ f(x) dx + ∫ g(x) dx.
Integration by Parts:
∫ u dv = u * v – ∫ v du, where u and v are differentiable functions.
These formulas are just a few examples of the wide range of algebraic functions that can be integrated. Integrating more complex functions may require using multiple techniques and approaches.
Also Check:
Integral formulae for Trigonometric functions
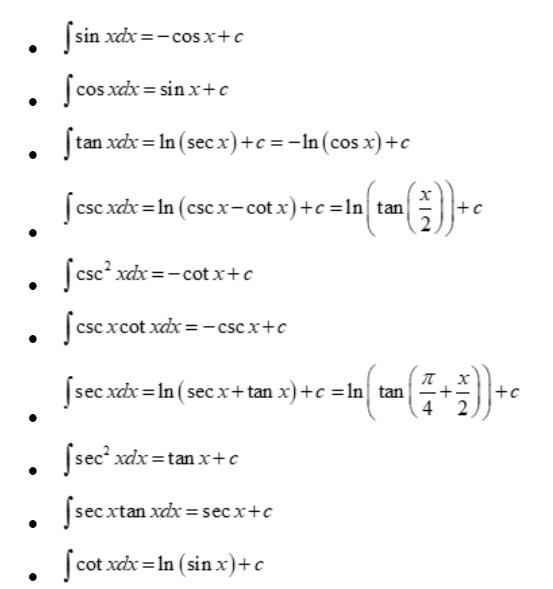
Integration of hyperbolic function

Integration of rational functions
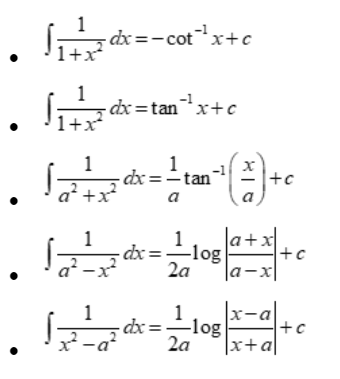
Integration of irrational function
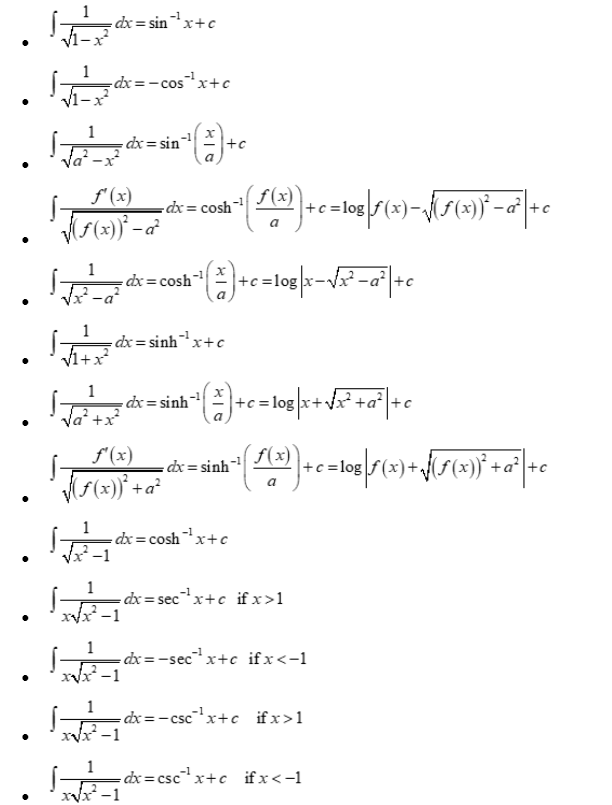
Special integrals
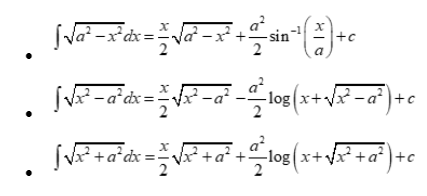
Integration by substitution related formula
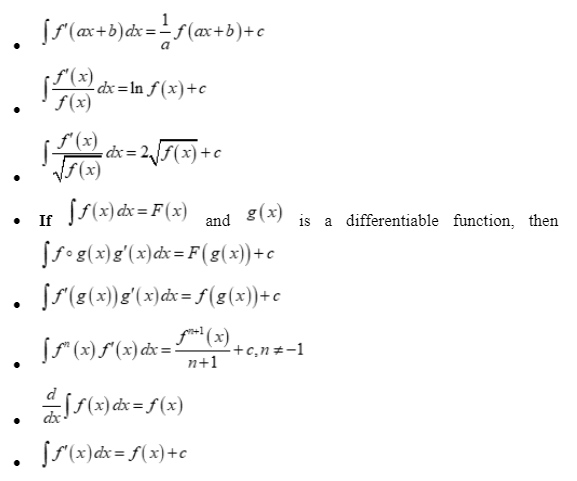
Integration formula by partial fractions
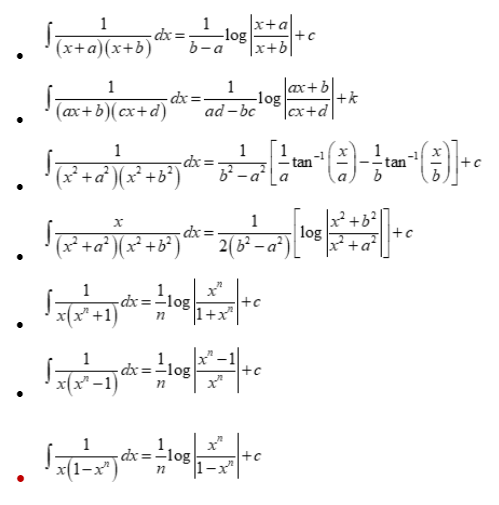
Integration by parts
If f(x)og(x)dx are any two functions, then ∫f(x).g(x)dx = ∫f'(x)g(x)dxdx
Proper choice of first and second function
- The first function is the function which comes first in the word ILATE
- If one of the two functions is not directly integrable, then take this function as the first function.
- If one of the function is not directly integrable, and there is no other function, then unity is taken as the second function.
Some Integral formulas using integration by parts
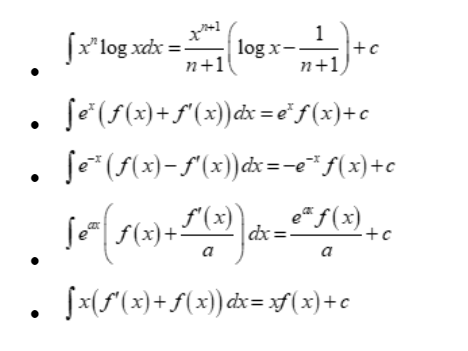
Integration formula for inverse trigonometric functions
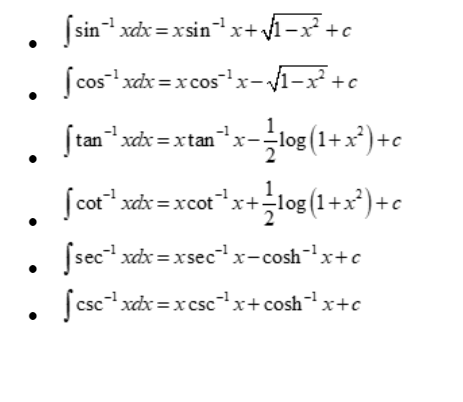
Solve some examples using the integration formulas mentioned earlier
Example 1: ∫ (3x^2 + 2x + 1) dx
Using the Power Rule:
∫ (3x^2) dx = (3 * x^(2+1))/(2+1) + C
= (3/3) * x^3 + C
= x^3 + C.
Using the Power Rule:
∫ (2x) dx = (2 * x^(1+1))/(1+1) + C
= x^2 + C.
Using the Power Rule:
∫ (1) dx = x + C.
Putting it all together:
∫ (3x^2 + 2x + 1) dx = x^3 + x^2 + x + C.
Example 2: ∫ (e^x + 5sin(x)) dx
Using the Exponential Integral:
∫ e^x dx = e^x + C.
Using the Trigonometric Integral:
∫ sin(x) dx = -cos(x) + C.
Since the integral of a sum is the sum of integrals:
∫ (e^x + 5sin(x)) dx = (e^x + C) + 5*(-cos(x) + C)
= e^x – 5cos(x) + C.
Example 3: ∫ (x^3 + 2x^2 – 2x + 5) dx
Using the Power Rule:
∫ (x^3) dx = (x^(3+1))/(3+1) + C = (1/4) * x^4 + C.
Using the Power Rule:
∫ (2x^2) dx = (2 * x^(2+1))/(2+1) + C = (2/3) * x^3 + C.
Using the Power Rule:
∫ (-2x) dx = -2 * (x^(1+1))/(1+1) + C = -x^2 + C.
Using the Power Rule:
∫ (5) dx = 5 * x + C.
Putting it all together:
∫ (x^3 + 2x^2 – 2x + 5) dx = (1/4) * x^4 + (2/3) * x^3 – x^2 + 5x + C.
These are just a few examples to illustrate the use of integration formulas. Remember, integration can involve more complex functions and may require multiple steps or special techniques in some cases.
Frequently asked questions about Integration formulas
What is the integration formula?
The integration formula gives a way to find the area under a curve or the accumulation of quantities. Common ones involve adding up tiny bits of areas or quantities.
What are the 4 types of integration?
There are four main types: Indefinite integration, Definite integration, Line integration, and Surface integration. Each serves different mathematical purposes.
Why is integration used?
Integration is used to find areas under curves, volumes of shapes, or accumulate quantities. It's essential in physics for understanding concepts like work and energy.
What is the meaning of integration?
Integration means combining parts to form a whole. In math, it refers to summing up small pieces to determine a total or area.
What is the use of integration?
Integration helps in various fields like physics, engineering, and economics. It's used to find quantities like total distance, area under a graph, or accumulated change.
What is integration?
Integration is a mathematical process that adds up tiny parts to find a total or area. It's like piecing together small sections to get the whole picture.









