Table of Contents
Introduction
The perimeter of a parallelogram is the length of the continuous line formed by its boundary. Its unit is the same as that of its sides. A quadrilateral is a closed shape made up of four line segments. A quadrilateral is called a parallelogram if its opposite sides are parallel and are of equal length. Some examples of a parallelogram are rhombus, rectangle, and square. Here are some properties of a parallelogram. In simple words, we can say that the perimeter of a parallelogram is equal to the sum of all its four sides.
Opposite sides are equal.
Opposite angles are equal.
Diagonals bisect each other.
Every two adjacent angles are supplementary.
In this article, we will learn how to find the perimeter of a parallelogram using some formulas. We shall also understand the applications of the perimeter of parallelogram formulas. We will explore the concept with the help of a few solved examples for a better understanding of the concept.
Parallelogram Formula
A parallelogram is a quadrilateral which has its opposite sides parallel and equal in length. The perimeter of the parallelogram is twice the sum of one pair of its adjacent sides.
Consider a parallelogram whose adjacent sides are of length ‘a’ and ‘b’.
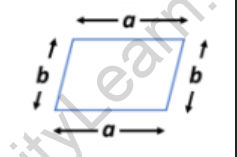
Thus, the perimeter of the parallelogram = a + b + a + b
= 2a + 2b
= 2(a + b)
For example,
If the adjacent sides of a parallelogram are 9 cm and 5 cm, then its perimeter is given by,
Perimeter of the parallelogram = 2(a + b)
= 2(9 + 5) = 2(14)
= 28 cm.
So, the perimeter of the parallelogram is 28 cm.
Alternatively, we can also use the formula:
Perimeter = 2(l + w)
In this formula, ‘l’ represents the length of the parallelogram, and ‘w’ represents its width.
It’s important to note that the perimeter of a parallelogram is always expressed in the same unit as the lengths of the sides.
The perimeter formula allows us to quickly determine the total length of the sides of a parallelogram, which is useful in various applications, such as calculating fencing requirements, estimating material quantities, or determining the distance around a given shape.
Also read: Parallelogram Formula
Solved Examples on Perimeter of a Parallelogram Formula:
Example 1: A parallelogram has two adjacent sides measuring 6 cm and 8 cm. Find the perimeter of the parallelogram.
Solution:
Using the formula for the perimeter of a parallelogram, P = 2a + 2b, where ‘a’ and ‘b’ are the lengths of the adjacent sides:
P = 2(6 cm) + 2(8 cm)
P = 12 cm + 16 cm
P = 28 cm
Therefore, the perimeter of the parallelogram is 28 cm.
Example 2: The length of one side of a parallelogram is 10 meters, and the width is 6 meters. Determine the perimeter of the parallelogram.
Solution:
Using the formula P = 2(l + w), where ‘l’ is the length and ‘w’ is the width of the parallelogram:
P = 2(10 meters + 6 meters)
P = 2(16 meters)
P = 32 meters
Hence, the perimeter of the parallelogram is 32 meters.
Frequently Asked Questions on Perimeter of a Parallelogram:
The rule for calculating the perimeter of a parallelogram is to add the lengths of all four sides. Since opposite sides of a parallelogram are equal in length, the formula for the perimeter simplifies to P = 2a + 2b, where a and b represent the lengths of two adjacent sides. Alternatively, we can use the formula P = 2(l + w), where l is the length and w is the width of the parallelogram. By adding the lengths of the sides, we can determine the total distance around the parallelogram, which gives us its perimeter.
The area and perimeter of a parallelogram are two distinct measurements. There is no direct mathematical relationship between them. The area represents the enclosed space within the parallelogram and is given by base x height, while the perimeter represents the total length of its boundary and is given by 2(Length + Width).
To find the missing perimeter of a parallelogram, you need to know the lengths of at least three of its sides. Here's how you can calculate the missing perimeter: Determine the lengths of the known sides of the parallelogram. Add the lengths of the known sides together to find the sum. Subtract the sum of the known sides from the total perimeter of the parallelogram to find the missing side.
No, not all parallelograms with the same perimeter have the same area. The area of a parallelogram depends not only on its perimeter but also on the dimensions of its sides and the angle between those sides. Parallelograms with different side lengths and angles can have the same perimeter but different areas. For example, consider two parallelograms with the same perimeter: one could have longer sides and acute angles, while the other could have shorter sides and obtuse angles. Despite having the same perimeter, the first parallelogram will generally have a larger area than the second parallelogram.
The relationship between the perimeter and width of a parallelogram is not fixed. Generally, increasing the width tends to increase the perimeter, while decreasing the width tends to decrease the perimeter. However, the specific relationship depends on the other dimensions and properties of the parallelogram.
We cannot find the perimeter of a parallelogram just using one side, but if we know the height and angle of the parallelogram as well, then we can find it. The perimeter of a parallelogram whose base is a, height is h, and one of the vertex angles is θ is 2a + 2h / sin θ.
The perimeter of a parallelogram is obtained just by adding all its sides. Since the opposite sides of a parallelogram are equal, it is sufficient to know its two adjacent sides to find the perimeter. But we may not be given with two adjacent sides always, instead, we may be provided with some other information about it to find its perimeter. If adjacent sides of a parallelogram a and b are given then apply the formula 2a + 2b to find its perimeter. If one of the sides of a parallelogram is a and its diagonals are x and y then apply the formula 2a + √(2x2 + 2y2 - 4a2) to find its perimeter. If the base of a parallelogram is a, its height is h, and one of its vertex angles is θ then apply the formula 2a + 2h / sin θ to find its perimeter.
The formula for the perimeter of a parallelogram when base and height are given along with an interior angle is: P = 2 (b +h/cos θ) where b = base, h = height of parallelogram with respect to base, θ is the interior angle. What is the rule for the perimeter of a parallelogram?
What is the relationship between the area and perimeter of a parallelogram?
How do you find the missing perimeter of a parallelogram?
Do all parallelograms with the same perimeter have the same area?
What is the relationship between perimeter and width?
How to Find the Perimeter of a Parallelogram with Missing Side?
How to Find the Perimeter of Parallelogram?
What is the perimeter of parallelogram using base and height?






