Table of Contents
A polygon is a two-dimensional geometric shape with straight sides. The formulas associated with polygons are used to calculate various properties such as the perimeter, area, interior angles, and diagonals of the polygon. The specific formulas depend on the type of polygon, including triangles, quadrilaterals, pentagons, hexagons, and so on. These formulas provide a systematic approach to determine the measurements and characteristics of polygons, enabling us to solve problems and analyze geometric shapes effectively.
What is Polygon?
A simple closed figure formed by line segments which are in the same plane is called a Polygon.
A polygon can have any number of sides, 3, 4, 5 or 100 or even more. Based on the number of sides, polygons have different names.
For example:
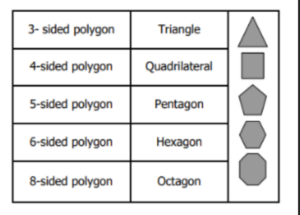
What are the types of polygons?
We know that a polygon is a simple closed figure made up of only line segments. Based on the number of sides or vertices in a polygon, they are known as a triangle, quadrilateral, pentagon and so on.
Let us look at some other types of polygons.
What are convex and concave polygons?
Based on how the vertices of a polygon point, there are two types:
(i) Convex polygon – It is a polygon in which any line segment joining any two
vertices of the polygon lies wholly in the interior of it.
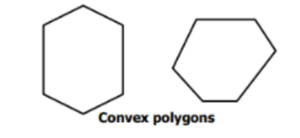
(ii) Concave polygon – It is a polygon in which at least one of the line segment joining
the vertices of the polygon lies outside the polygon

What are Regular and Irregular polygons?
Based on the length of the sides, a polygon is classified as:
(i) Regular polygon – It is a polygon that has all its sides of equal length.
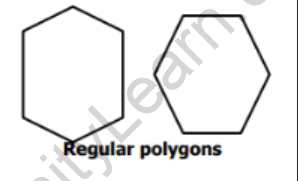
(ii) Irregular polygon – It is a polygon that does not have all sides of equal length.

Polygon Formula:
1: Interior Angles Sum Property:
The angle sum of a polygon for interior angles can be determined by multiplying the number of triangles it consists of, by 180°
The angle sum of a polygon for interior angles can be determined by multiplying the number of triangles it consists of, by 180°

For example, quadrilateral ABCD is made up of triangles ABC and BCD.
- Sum of angles of triangle ABC = 180°
Sum of angles of triangle BCD= 180°
- Therefore, sum of angles of triangle ABC + BCD = 180 + 180
That is, the sum of angles of quadrilateral ABCD = 180° x 2
The Polygon Formulas are:
| Aspect | Formula |
|---|---|
| Sum of Interior Angles (n-sided polygon) | 180°(n-2) |
| Number of Diagonals (n-sided polygon) | [n(n-3)]/2 |
| Interior Angle Measurement (Regular n-sided) | [(n-2)180°]/n |
| Exterior Angle Measurement (Regular n-sided) | 360°/n |
um of angles of a pentagon
A pentagon can be divided into 3 triangles. Hence, the sum of its angles = 180° x 3

Let us look at the relationship between the number of sides of a polygon and its angle sum.

This can be generalized as:
The sum of angles of a polygon having ‘n’ sides is given by (n – 2) x 180°.
2: Number of diagonals of a polygon:
Diagonals of a polygon are line segments connecting non-adjacent vertices. The number of diagonals in a polygon can be found using the formula n(n-3)/2, where n is the number of sides. For instance, a hexagon has six sides, so the number of diagonals is (6(6-3))/2 = 9.
Solved Examples on Polygon Formula:
Example 1: Determine the sum of interior angles and the number of diagonals in an octagon.
Solution:
Sum of interior angles = (n – 2) × 180 degrees = (8 – 2) × 180 = 1080 degrees
Number of diagonals = n × (n – 3) / 2 = 8 × (8 – 3) / 2 = 20 diagonals
Example 2: Calculate the area of an irregular triangle with a base length of 12 cm and a height of 8 cm.
Solution:
Area of a triangle = (1/2) × base × height = (1/2) × 12 × 8 = 48 cm²
Example 3: Find the perimeter of a quadrilateral with side lengths 5 cm, 6 cm, 7 cm, and 8 cm.
Solution:
Perimeter of a quadrilateral = sum of all side lengths = 5 + 6 + 7 + 8 = 26 cm
Example 4: Determine the number of diagonals in a decagon.
Solution:
Number of diagonals = n × (n – 3) / 2 = 10 × (10 – 3) / 2 = 35 diagonals
Frequently Asked Questions on Polygon Formula:
1: What is sum of all angles of polygon?
Answer: The sum of all angles in a polygon is given by the formula (n-2) × 180 degrees, where n represents the number of sides or vertices of the polygon.
2: What is the formula for finding the diagonals of a polygon?
Answer: The formula for finding the number of diagonals in a polygon is given by the expression n × (n-3) / 2, where n represents the number of sides or vertices of the polygon. It calculates the number of line segments that can be drawn connecting any two non-adjacent vertices of the polygon.
3: What is the formula of area of polygon?
Answer: The formula for calculating the area of a polygon depends on the type of polygon. For regular polygons, the formula is (1/2) × apothem × perimeter, where the apothem is the distance from the center of the polygon to any side, and the perimeter is the sum of all the side lengths. For irregular polygons, the area can be determined by dividing the polygon into smaller, regular shapes and summing their individual areas.
4: Which polygon has 20 diagonals?
Answer: A polygon with 20 diagonals is an octagon. An octagon has eight sides and using the formula for calculating the number of diagonals in a polygon, which is n × (n-3) / 2, we can substitute the value of n as 8. Thus, the octagon has 8 × (8-3) / 2 = 20 diagonals.
5: What is the formula for the length of diagonal?
Answer: The formula for calculating the length of a diagonal in a polygon depends on the specific polygon and the information given. However, if the polygon is regular and you know the side length, you can use trigonometric functions to calculate the length of a diagonal.
6: What polygon has 7 diagonals?
Answer: A polygon with 7 diagonals is a pentagon (a polygon with five sides). By using the formula for calculating the number of diagonals in a polygon, which is n × (n-3) / 2, we can substitute the value of n as 5. Therefore, a pentagon has 5 × (5-3) / 2 = 7 diagonals.
7: What is the difference between regular and irregular polygons?
Answer: Regular polygons have equal side lengths and angles, while irregular polygons have varying side lengths and/or angles. Regular polygons exhibit symmetry and have a uniform shape, whereas irregular polygons lack symmetry and do not have a consistent shape.
8: What is the difference between concave and convex polygons?
Answer: Concave polygons have at least one interior angle greater than 180 degrees, with “caved-in” or “hollow” portions. Convex polygons have all interior angles less than 180 degrees, with no “caved-in” portions and outward-pointing vertices. Concave polygons exhibit inward curvature, while convex polygons exhibit outward curvature.
Polygon Formula FAQs
How do you find the sides of a polygon?
To find the sides of a polygon, count the number of line segments that form its shape.
How do you solve a polygon formula?
You solve a polygon formula by using the specific mathematical rule or equation that corresponds to the shape's characteristics.
What is polygon in math 7?
In math, a polygon with 7 sides is called a heptagon.
What is the formula for the area of a polygon with n sides?
The formula for finding the area of a polygon with n sides varies based on the shape's type and dimensions.
What is the area of a polygon with 5 sides?
The area of a 5-sided polygon depends on its shape and dimensions; a specific formula is needed.
What is the formula for regular polygon?
A regular polygon is one with equal sides and angles, making it easier to calculate its properties.
Which polygon has diagonals?
Many polygons have diagonals, but squares, rectangles, and triangles are common examples.
What polygon has 20 diagonals?
A polygon with 20 diagonals is typically a dodecagon (12 sides) or a polygon with a large number of sides to have that many diagonals.









