Adjacency Matrix – Definition, Properties and Solved Questions

An adjacency matrix is a square matrix used to represent a finite graph. It provides a simple and systematic way to describe the connections between the nodes of a graph. In this article, we will study more about the adjacency matrices, their properties and more.

Adjacency Matrix

The adjacency matrix is a square matrix of n x n size. In the adjacency matrices, the number of nodes in the graph is equal to n and is used for representing the connections of the edges in a graph. Each element in the matrix indicates whether a pair of vertices is connected by an edge.

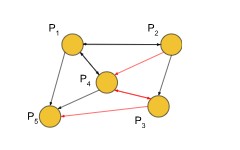
What is an Adjacency Matrix?

To put it in simpler terms, the adjacency matrix definition can be visualized as a finite graph having rows and columns. You can also create a directed graph or un-directed graph through the adjacency matrix concept.

The adjacency matrix is often referred to as a connection matrix or a vertex matrix. It falls under the syllabus of Class 12 Maths and can be defined as a matrix with rows and columns, which are usually used to represent simple labeled graphs. The elements at (Vi, Vj) are either 0 or 1, depending on whether Vi and Vj are adjacent or not. In simple words, an adjacency matrix is a more compact way of representing finite graphs with n vertices through an m x m matrix M.

One Stop Solutions for School Exam Preparation

Boost your school preparation with our comprehensive guide for CBSE, ICSE, and State Board exams. Get all the resources you need in one place and excel in your academic journey. Discover the ultimate one-stop solution at Infinity Learn today!

Key Properties of an Adjacency Matrix

An adjacency matrix is also known as a vertex matrix. It is an array of numbers that represents the relationships within a graph. The properties of the graph are often reflected in the properties of its adjacency matrix. Below mentioned are some key properties of the Adjacency Matrix:

• The powers of the adjacency matrix can provide valuable insights about the graph. Specifically, the entries of the matrix powers give information about paths within the graph.
  Theorem: Let A be the adjacency matrix of a graph. The element at position (i, j) in the matrix Aⁿ counts the number of n-step walks from vertex i to vertex j.
• Spectral graph theory studies the eigenvalues of the adjacency matrix. For a k-regular graph with adjacency matrix A and an all-ones column vector v in Rⁿ, the i-th entry of Av equals the sum of the entries in the i-th row of A. This sum represents the number of edges emanating from vertex i, which is exactly k.
• Two graphs are considered isomorphic if one can be obtained from the other by relabeling its vertices. Although isomorphic graphs may not have identical adjacency matrices due to vertex labeling differences, their adjacency matrices are closely related.
  Theorem: Let G and H be graphs with n vertices and adjacency matrices A and B, respectively. Graphs G and H are isomorphic if and only if there exists a permutation matrix P such that B = PAP^-1.
• For simple graphs without self-loops, the diagonal entries of the adjacency matrix must be zero. In undirected graphs, the matrix is symmetric along its main diagonal, meaning that an edge between two nodes is represented by a 1 in both the (row of the first node, column of the second node) and (column of the first node, row of the second node) positions.
• The adjacency matrix is a square array where each row represents outgoing nodes (out-nodes) associated with a graph, and each column represents incoming nodes (in-nodes). For undirected graphs, this symmetry ensures that the graph’s connections are mirrored across the main diagonal.
• When the adjacency matrix is multiplied by itself (squared), any non-zero values at the (i, j) position in the resulting matrix indicate that there is a path of length two between vertices V_i and V_j. However, this operation does not provide direct information about the exact distance between these vertices.
• Although adjacency matrices are powerful tools for visualising connections within a graph, they have some limitations. For instance, while they can indicate the existence of paths, they do not directly convey the actual distances or other specific attributes like estimated waiting times between nodes.

How to Build an Adjacency Matrix?

There are some steps you must follow in order to construct an adjacency matrix for a graph in a very easy and simple manner:

In case we possess a graph called G having n quantities of vertices, then the vertex matrix (n x n) can be expressed as:

Where the value a_ij equals the number of edges from the vertex i to j. For an undirected graph, the value of a_ij = a_ji for all i, j, so that the adjacency matrix becomes a symmetric matrix.

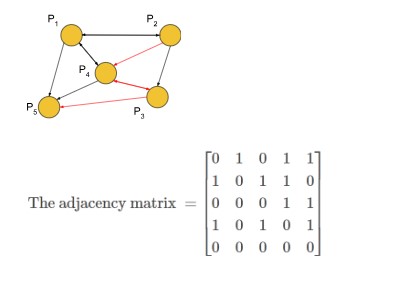
Therefore, Let G be a graph with vertex set {v₁, v₂, v₃, . . . , v_n}. Then the adjacency matrix of G is the n × n matrix that has a 1 in the (i, j)-position if there is an edge from v_i to v_j in G. And it will have a 0 in the (i, j)-position otherwise.

From the given directed graph, the adjacency matrix is written as

Online Mock Test

Boost Your Preparation With Our Free Online Mock Tests For IIT-JEE, NEET And CBSE Exams

Advantages of Using Adjacency Matrix

• Understanding an adjacency matrix is clear and simple.
• One can easily remove or add edges.
• The adjacency matrix provides constant time access to check the presence or absence of any edge between two vertices.

Disadvantages of Using Adjacency Matrix

• It uses O(N²) space, which can be wasteful for graphs with few edges.
• Finding all neighbors of a vertex takes O(N) time, which can be slow for large graphs.

Adjacency Matrix FAQs