Table of Contents
Algebraic Identities are the basis of Algebra. These identities and their applications make it easier for the students to solve algebraic linear equations. This helps students get rid of confusing long calculations. They can easily get the desired result by using these worldwide accepted Algebraic Identities.
These algebraic Identities are useful for both students and aspirants appearing for the competitive examinations. They must have a good grasp of these algebraic Identities that will be discussed in this article. Students can also download the Algebraic Identities Charts in PDF format using the link provided in the article.
What are Algebraic Identities?
In Algebra, the algebraic Identities are the equations used to perform the calculations in simple steps. The left-hand side of these equations is always equal to the right-hand side.
For example, if we need to solve the given linear equation, then instead of solving we can apply an Algebraic Identity.
Consider the following linear equation:
7² – 5²
Therefore, we apply the algebraic identity:
a² – b² = (a+b) (a-b)
Therefore, the equation becomes,
7² – 5² = (7+5) (7-5)
7² – 5² = (12) (2)
7² – 5² = 24
Let’s verify:
7² – 5² = 49 – 25 = 24
Therefore, the identity gave an accurate result.
Standard Algebraic Identities
There are a number of algebraic equations in mathematics. The major algebraic identities in algebra are discussed below:
- (a+b)² = a²+2ab+b²
- (a-b)² = a²- 2ab+b²
- (a+b)(a-b) = a²-b²
- (x+a)(x+b) = x²+x(a+b)+ab
- (a+b)³ = a³+b³+3ab(a+b)
- (a-b)³ = a³-b³-3ab(a-b)
- (a+b+c)² = a²+b²+c²+2(ab+bc+ca)
- a³+b³+c³-3abc = (a+b+c)(a²+b²+c²-ab-bc-ca)
Types of Algebraic Identities
There are multiple types of algebraic identities depending on the number of variables used or the type of question asked. A few types of algebraic identities are discussed below.
Two-Variable Identities
The following written algebraic identities involve two variables. Two variable identities can be verified easily by expanding the squares or cubes and multiplication of polynomials.
- (a+b)²= a²+2ab+b²
- (a-b)² = a²- 2ab+b²
- (a+b)(a-b) = a²-b²
- (a+b)³ = a³+b³+3ab(a+b)
- (a-b)³ = a³-b³-3ab(a-b)
Three Variable Identities
The following written algebraic identities involve three variables. These can be easily verified with the expansion of squares or cubes and the multiplication of polynomials.
- (a+b+c)² = a²+b²+c²+2(ab+bc+ca)
- a²+b²+c² = (a+b+c)²- 2(ab+bc+ca)
- a³+b³+c³-3abc = (a+b+c)(a²+b²+c²-ab-bc-ca)
- (a+b)(b+c)(c+a) = (a+b+c)(ab+ac+bc)-2abc
Factorisation Identities
Algebraic Identities help in factoring Algebraic expressions. With the use of these identities, many higher Algebraic expressions like a⁴-b⁴ can be easily factored. Below is the list with the help of which polynomials can be factored:
- a²-b² = (a-b)(a+b)
- x²+x(a+b)+ab = (x+a)(x+b)
- a³-b³ = (a-b)(a²+ab+b²)
- a³+b³ = (a+b)(a²-ab+b²)
Proof of Algebraic Identities
The proof of the algebraic identities will help to better understand each of these identities. Take a look at the following proofs of the basic algebraic identities:
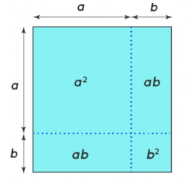
Proof of (a+b)² = a²+2ab+b²
- Basically, (a+b)² is (a+b)×(a+b).
- It can be visualised as a square with sides (a+b) and area (a+b)².
- The square having a side (a+b) has four areas a², ab, ab, and b².
- The sum of all these areas a²+ab+ab+b² gives the area of a big square (a+b)².
- Therefore, (a+b)² = a²+2ab+b²
Proof of (a+b)(a-b) = a²-b²
- Here, the main objective is to find the value of a²- b².
- It can be taken as the difference of the area of two squares with sides a units and b units respectively.
- It will be equal to the sum of the areas of two rectangles [i.e. a(a-b) + b(a-b)]as shown in the below-given figure.
- Therefore, a2 – b2 = a(a-b) + b(a-b)
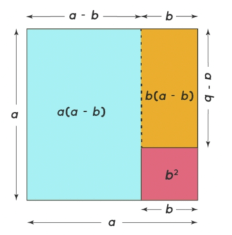
Brief explanation: The length and breadth of one rectangle are a unit and (a-b) units. The length and breadth of another rectangle are (a-b) units and b units. We will find the areas of the two rectangles and the sum of the areas to obtain the result value.
The areas of both the rectangles are (a-b) × a = a(a-b), and (a-b)×b= b(a-b).
The sum of the areas will be taken to obtain the resultant expression:
a(a-b) + b(a-b) = (a-b)(a+b)
Hence, a²-b² = (a-b)(a+b)
Do Check: Trigonometric Identity
Proof of (a-b)² = a²- 2ab+b²
Assume (a-b)² as the area of the square whose length is (a-b). To understand this, let there be a large square whose area is a². Reduce the length of all the sides by b, it will become a-b.
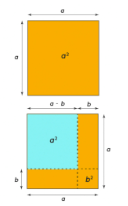
- From a², remove extra bits to the left with (a-b)².
- In the above figure, (a-b)² is represented by the blue region.
- To get the blue square, from the larger orange square, subtract the vertical and horizontal strips having the area ab.
- If we remove the ab twice, the overlapping square at the bottom will also get removed. So, we add b². We have, (a-b)² = a²- ab- ab+b².
Therefore, this proves the algebraic identity
(a-b)² = a²- 2ab+b².
Solved Questions on Algebraic Identities
Example 1: Expand (4x+y)²
Ans. To expand the given expression, substitute a= 4x and b= y in (a+b)²= a²+2ab+b²
(4x+y)²= (4x)²+2(4x)(y)+ (y)²
= 16x²+8xy+ y²
Example 2: Find the value of a³+b³+c³ when a+b+c= 0.
Ans. In one of the above-written identities,
a³+b³+c³-3abc = (a+b+c)(a²+b²+c²-ab-bc-ca)
Substitute (a+b+c) = 0,
a³+b³+c³-3abc =0(a²+b²+c²-ab-bc-ca)
a³+b³+c³-3abc = 0
a³+b³+c³ = 3abc
Example 3: Factorize (x⁶-1)
Ans. (x⁶-1) can be written as (x³)²-1²
It resembles the identity a²-b² = (a-b)(a+b)
Where a= x³ and b= 1
So, x⁶-1= (x³+1)(x³-1)
FAQs on Algebraic Identities
What are algebraic identities?
Algebraic identities are equations that hold true for all values of the variables involved. They are used to simplify algebraic expressions and solve equations more efficiently. Common examples include the expansion of squares and cubes, such as (a + b)2 = a2 + b2 + 2ab
Why are algebraic identities important?
Algebraic identities are important because they allow us to simplify complex algebraic expressions, making it easier to perform calculations and solve equations. They are widely used in various fields of mathematics, including algebra, calculus, and number theory.
How can I apply algebraic identities in problem-solving?
To apply algebraic identities in problem-solving, identify the structure of the expression and match it to a known identity. For example, if you encounter an expression like 9x2 - 16, you can recognize it as a difference of squares and factor it as (3x + 4)(3x - 4)
What is the difference between an algebraic identity and an equation?
An algebraic identity is true for all values of the variables involved, while an equation is true only for specific values of the variables. For example, the identity (x + y)2 = x2 + y2 + 2xy holds for any x and y whereas the equation x + 2 = 5 is only true when x = 3









