Table of Contents
Introduction to Antilog Table
The antilog table is a useful tool for finding the antilogarithm of a number. Antilogarithm is the inverse of the logarithm function. Just as a logarithm helps simplify calculations by turning multiplication into addition, the antilog performs the reverse operation, transforming the result back into its original form.
What is an Antilog?
The antilog is a short form for “antilogarithm”. It is used to reverse the effect of taking a logarithm. For instance, if you have the logarithm of a number and want to find the original number, you use the antilog. This process is especially useful when you’re working with large numbers and need to simplify complex calculations.
How the Antilog Table Works?
The antilog table provides values for the antilogarithm function. Firstly, you take the logarithm of the number you’re working with. Once you have the value of the logarithm, use the antilog table to find the number that corresponds to this logarithmic value. The value from the antilog table gives you the simplified result.
The Antilog of Positive and Negative Numbers
For Positive Numbers: The antilog table provides values for the antilogarithms of positive numbers. By looking up the log value in the table, you can find the corresponding number easily.
For Negative Numbers: If you have a negative logarithm, you need to consider the decimal point in the antilog calculation.
For example, an antilog of -2 is 0.01.
Components of the Antilogarithm Table
The antilogarithm table is organised into three distinct blocks. Each of these blocks serves a specific purpose in finding the antilogarithm of a number. It is necessary to understand the algorithm table briefly to calculate the antilog effectively.
1. Main Column (First Block)
This block lists numbers from 0.00 to 0.99. It represents the first part of the decimal value in the logarithm you are looking up. The main column provides the base values for the antilogarithm calculations. These values correspond to the whole number part and the first two decimal places of the logarithmic value.
2. Differences Columns (Second Block)
This block contains digits from 0 to 9, showing the differences for each value in the main column. The differences columns are used to fine-tune the antilogarithm value. They help you adjust the base value from the main column to get the precise result, by adding the appropriate value from these columns based on the decimal part of the logarithm.
3. Mean Differences Columns (Third Block)
This block shows digits from 1 to 9, representing mean differences that are used for interpolation. The mean differences columns help in refining the results even further when the logarithmic value falls between the numbers listed in the main column and the differences columns. This block is used for more accurate calculations by accounting for fractional values.
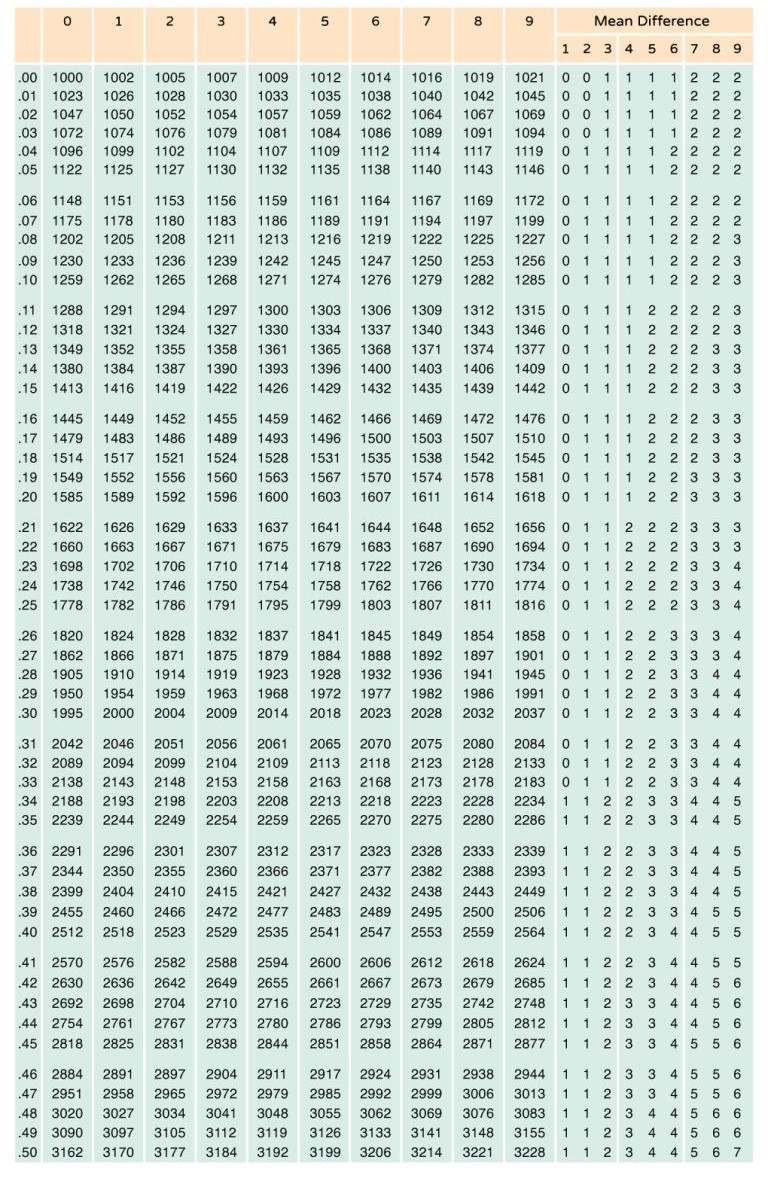
How to Use the Antilogarithm Table
Below is a step-by-step guide to help you in using the antilog table. you must follow these steps to find the antilog of the given problem.
Step 1: Start with the logarithmic value you want to find the antilog of.
For example, if you need to find the antilog of 2.45, note that the value is split into 2 (the integer part) and 0.45 (the decimal part).
Step 2: Locate the row corresponding to the integer part of your logarithmic value (in this case, 2.00 to 2.99) in the main column.
Step 3: Look at the decimal part (0.45) and find the corresponding value in the differences columns.
For example, if the decimal part is 0.45, find the value under 5 (from the differences columns).
Step 4: If needed, use the mean differences columns to adjust your result for more precision. This step is especially useful if the decimal part of your logarithm falls between values listed in the table.
Step 5: Add the values from the main column, differences columns, and mean differences columns to get the final antilogarithm result.
Solved Examples on Antilog
Example 1: Find: Antilog(2.345)
Ans. Step 1: Separate Characteristic and Mantissa
Characteristic: 2
Mantissa: 0.345
Step 2: Use the Mantissa to Find the Base Value
- Look up the row corresponding to 0.34 (the first two digits of the mantissa) in the antilog table.
- Find the column corresponding to the third digit (5) in the same row.
- Suppose the table shows the value 2178 at row 0.34 and column 5.
Step 3: Refine the Value Using Mean Differences
- The fourth digit of the mantissa is 0, so the mean difference is 0.
- Add this to the base value from Step 2:
2178+0=2178
Step 4: Adjust the Decimal Point
Place a decimal point after the first digit: 2178 becomes 21.78
Step 5: Multiply by 10 Characteristic
Multiply by 102 (since the characteristic is 2):
Therefore, Antilog(2.345)=21.78×102 =2178
Example 2: Find the antilog of (-1.678)
Ans. Step 1: Separate Characteristic and Mantissa
Characteristic: -1
Mantissa: 0.678
Step 2: Convert to Positive Mantissa
Convert the logarithmic value to a positive mantissa:
Antilog(-1.678) = 1/101.678
is the antilog of the positive value 1.678.
Step 3: Use the Mantissa to Find the Base Value
- Look up the row corresponding to 0.67 in the antilog table.
- Find the column corresponding to the third digit (8) in the same row.
- Suppose the table shows the value 4771 at row 0.67 and column 8.
Step 4: Refine the Value Using Mean Differences
- The fourth digit of the mantissa is 0, so the mean difference is 0.
- Add this to the base value from Step 3:
4771+0=4771
Step 5: Adjust the Decimal Point
Place a decimal point after the first digit:
4771 becomes 47.71
Step 6: Multiply by 10 Characteristic
Since the characteristic is -1, take the reciprocal:
Antilog(−1.678)= 47.7/10 =4.771
Therefore, Antilog(−1.678) =4.771
Practice Questions on Antilog
- Find the antilog of −2.345
- Find the antilog of 0.456
- Find the antilog of −0.789
- Find the antilog of 2.456
- Find the antilog of −3.123
- Find the antilog of 1.234
- Find the antilog of −0.567
- Find the antilog of 0.789
- Find the antilog of 3.456
- Find the antilog of −1.234
FAQs on Antilog
What is an antilog?
The antilog, or antilogarithm, is the inverse function of the logarithm. If log(x)=y, then Antilog(y)=x. In simpler terms, while the logarithm converts a number into its logarithmic form, the antilog converts it back to its original number.
How do I calculate the antilog of a number?
To calculate the antilog of a number, follow these steps: Separate the number into its characteristic (integer part) and mantissa (decimal part). Use the antilog table to find the base value corresponding to the mantissa. Combine this base value with the characteristic by placing a decimal point and multiplying by 10 Characteristic
What is the difference between a Major Arc and a Minor Arc?
Minor Arc: An arc that measures less than 180° of the circle’s circumference. It is the shorter of the two arcs connecting the same endpoints. Major Arc: An arc that measures more than 180° of the circle’s circumference. It is the longer arc connecting the same endpoints.
Can I find the antilog without using a table?
Yes, you can use the formula Antilog(x)=10x to find the antilog of a number. For non-integer values or complex cases, a scientific calculator or computational tool is often used to calculate 10 x directly.









