Table of Contents
Area of a Circle: The area of a circle is the total space enclosed within the boundary of a circle. The formula used to calculate the area of a circle is πr², where, r is the radius of the circle. The unit of the area of a circle is m², cm², etc. In this article, we will discuss the circle, the surface area of a circle, and its perimeter.
Area of a Circle and Perimeter of a Circle
A circle is a two-dimensional geometrical shape. It is the set of all the points in the plane, that are equidistant from a selected point called the center of the circle. The fixed distance from the center is the radius of the circle.
A circle is a 2-D shape that only has an area and perimeter. Unlike the 3 dimensional shapes, a circle doesn’t have volume. Some common examples of the circle from our daily life are wheels, pizzas, etc.
Definition of Radius
- A radius is defined as a line joining the center of the circle to the outer boundary of the circle. It is represented by ‘r’.
- The radius plays a very important role in calculating the area and the perimeter/ circumference of the circle.
Definition of Diameter
The line that divides the circle into two equal parts is the diameter of a circle. Diameter is the double the radius.
i.e. d = 2r
We can calculate the radius of the circle if the diameter of a circle is given.
r= d/2
Also Check: Surface Area of Circle Formula
The Perimeter of a Circle
- The perimeter of any closed figure is defined as the length of its boundary.
- The perimeter of a circle is also known as the “Circumference of a Circle”.
- If the circle is opened in a straight line, the length of that straight line is the perimeter of the circle.
- To calculate the circumference of a circle, the value of pi (π) is required.
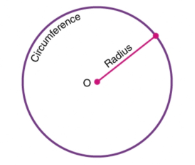
The circle with the center O and radius r is shown in the figure:
Now the perimeter of a circle is equal to the length of the boundary of a circle. The length of the rope that will wrap around the boundary of the circle will be equal to the circumference. The perimeter of the circle can be measured by using the formula:
Circumference = 2πr , Where r is the radius of the circle.
Properties of a Circle
- Circles which have equal radius are congruent.
- Circles having different radii appear to be similar.
- Chords equidistant from the center are of the same length.
- All the points on the circle are equidistant from the center point of the circle.
- The longest chord of the circle is the diameter.
- The diameter cuts the circle into two equal arcs. Each arc is a semicircle.
Also Check: Area of A Sector of A Circle Formula
Area of a Circle Model
The area of a circle is the space within the boundary of a circle. The formula for the area of a circle is πr², where r is the radius of the circle. The unit of the area of a circle is m², cm², etc.
The following figure represents the area of a circle.
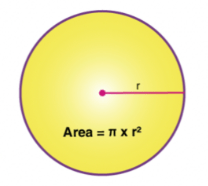
All the geometrical shapes have their own area. This area can be considered as the region occupied by the shape in a two-dimensional plane.
The area of a circle is the area covered by one complete cycle of the radius in a two-dimensional plane in the form of a circle. We use the formula discussed below to calculate the area of the circle.
Area of a Circle Formula
Below is the figure of the circle with radius r and center O from the boundary of the circle.
The area of the circle is the product of pi and the square of the radius, written as:
Area of a circle = πr² square units, Where the Value of π= 22/7 or 3.14, and r is the radius of a circle.
Also Check: Area of Quadrant
Derivation of the Area of a Circle
The area of a circle can be derived by two methods:
- Determining the area of a circle using rectangles.
- Determining the area of a circle using triangles.
Let’s discuss both methods for the derivation of the Area of a circle.
Using Areas of Rectangles
The circle is divided into 16 equal parts as shown in the below given figure.
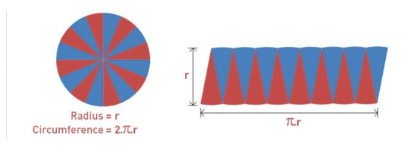
The area of a circle will be equal to the parallelogram-shaped figure which is formed by the parts divided from the circle. The red color is the half circumference, and blue will be the other half circumference. If the divided parts from the circle are increased, the parallelogram will seem like a rectangle whose length will be equal to πr and whose breadth is r.
So, the area of a rectangle will be the area of a circle.
A= π×r×r
A= πr²
Using Area of Triangles
The given figure shows the circle with radius r filled with concentric circles. Cut the circles along the indicated line. After spreading the lines, the result will be a triangle. The base of a triangle will act as the circumference of a circle and height will be the radius of the circle.
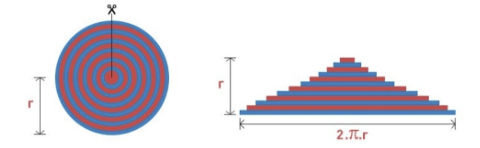
Therefore, the area of the triangle will be equal to the area of the circle.
A= 1/2×base×height
A= 1/2×2πr×r
A= πr²
Surface Area of a Circle
A circle is the 2-D representation of a sphere. The surface area of a circle is the total area taken inside the boundary of the circle. When we find the area of a circle, it means the area of a circle itself.
When the radius, diameter, or even the circumference of a circle is given, we can calculate the surface area of a circle using the formula, A= πr².
The surface area of a circle is represented in square units.
How to find the Area of a Circle?
There can be a number of ways to find the area of a circle. The three most common ways are discussed below.
Area of a Circle using a Radius
The area of a circle is calculated by using the formula:
A= πr², Where r is the radius of the circle.
Solved Example: Find the area of a circle if the radius is 7cm.
Solution: If the radius of the circle is 7cm, then the area of the circle will be:
A= π(7)²
A= 22/7×7×7
A= 154 sq. cm.
Area of a Circle using a Diametre
The area of a circle is calculated by using the formula:
A= πr², Where r is the radius of the circle.
We know that r=d/2
Therefore, the formula used to calculate the area of a circle becomes as:
A= πd² /4
Solved Example: Find the area of a circle if the diameter of the circle is 4cm
Solution: If the diameter of the circle is 4cm, then the area of the circle will be:
A= π(4)² /4
A= 22/7×4×4 / 4
A= 88/7
A= 12.57 sq. cm.
The area of a Circle if the Circumference is given
The area of a circle can also be found if the circumference of a circle is given.
As the circumference of a circle is 2 times the product of π and the radius of a circle.
C= 2πr
From this, we can find the radius of the circle.
r= C/2π
Once we know the value of the radius, we can find out the area of the circle.
FAQs on Area of Circle
Find the radius of a circle whose area is given 153.42 sq. cm.
A= π r² 153.42= πr² 153.42= 3.14×r² r²= 153.42/3.14 r²= 48.85 r = 6.98 cm.
Find the circumference and area of the circle whose radius is 14 cm.
A= πr² A= 22/7× 14× 14 A= 616 cm² Circumference= 2πr = 2×22/7× 14 = 88 cm
How to calculate the area of a circle if the diameter of a circle is given?
The diameter of a circle is two times the radius. Therefore, the area of the circle is π/4 times the square of the diameter of a circle. The formula of the area of a circle, if the diameter of a circle is given is: A=π/4 × diameter ²









