Table of Contents
The Area of the Trapezium is precisely the area covered by the figure of the trapezium in the two-dimensional plane. It is measured in square units. The trapezium is a 2D shape and is categorised as a quadrilateral figure. Similar to other geometrical figures like squares, circles, triangles and more, it also has its own formulas to find area, perimeter and volume along with its properties. The article below discusses the area of the trapezium along with its derivation and examples for better understanding of the students.
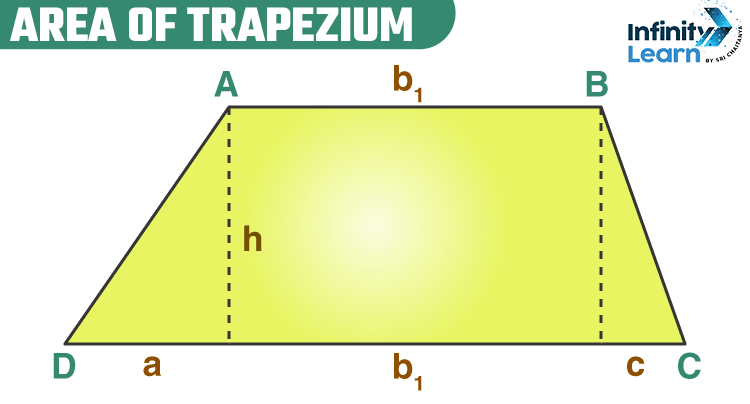
What is the Area of Trapezium?
The trapezium is a quadrilateral figure which has four sides and one set of parallel sides. The area of the trapezium is calculated as the region covered between these four sides. The area of the trapezium depends proportionally on the length of parallel sides and the height of the trapezium.
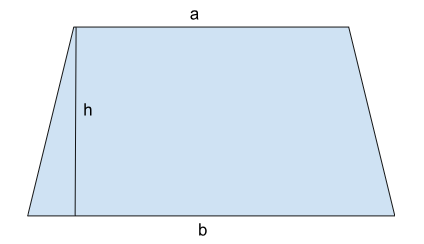
Area of Trapezium Formula
The Area of the Trapezium Formula can be calculated using the following formula.
Area of trapezium = ½ h (a+b)
Where a and b are the lengths of parallel sides, and h is the height of distance between the parallel lines.
Derivation of Area of a Trapezium
To compute the area of the trapezium follow the following steps:
We know that the area of trapezium is equal to the sum of the areas of two triangles and the area of a rectangle.
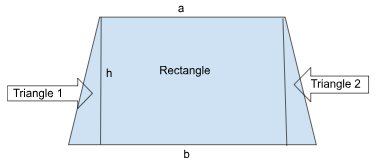
Therefore area of trapezium = area of triangle 1 + area of rectangle + area of triangle 2
=> A= ah/2 + b1h + ch/2
=> A= (ah + 2b1h + ch) /2
Simplifying the equation we get,
=> A= h/2(a + 2b1 + c)
=> A= h/2[b1 + (a + b1 + c)]
Longer base of trapezium be b2
Therefore, (a + b1 + c) = b2
=> A= h/2[b1 + b2]
Therefore the area of the trapezium with base b1 b2 and height h is calculated using the formula, A= h/2[b1 + b2]
How do you calculate the Area of the Trapezium?
To find the area of the trapezium, follow the below mention:
Step 1: find the dimensions of the given trapezium
Step 2: add the length of the parallel sides.
Step 3: multiply the height of the trapezium with the sum of The parallel sides obtained.
Step 4: now divide the obtained value by 2.
The obtained value at step 4 is the area of the trapezium.
Basic concept about Trapezium
- The pair of parallel sides of the trapezium are called the base of the trapezium. Whereas non-parallel sides are known as pillars of the trapezium or legs of the trapezium.
- The line segment connecting the middle points of the non-parallel sides of the trapezium is known as the mid-segment of the trapezium.
- If a line segment is drawn between two parallel sides of the trapezium, conducting both sides from their midpoint, respectively, divides the triangle into unequal parts.
- If two parallel sides of a trapezium are equal, then they form equal angles on the bases. The trapezium formed in this case is known as isosceles trapezium. The concept of the isosceles trapezium is similar to the concept of an isosceles triangle.
Properties of a Trapezium
- Just like in other four-sided shapes, the total of all four angles in a trapezium adds up to 360 degrees.
- A trapezium has two sides that run parallel to each other and two sides that are not parallel.
- In a regular trapezium, the diagonals intersect and split each other into two equal parts.
- The length of the mid-section (a line connecting the midpoints of the parallel sides) is half the sum of the lengths of the parallel sides in a trapezium.
- When you examine two pairs of angles in a trapezium, specifically those formed between the parallel sides and one of the non-parallel sides, their combined angle measurements always equal 180 degrees.
Applications of Trapezium
The idea is frequently employed in physics and math calculations. It forms the foundation for deriving motion equations as presented in the 9th-grade CBSE science textbook. The combination of physics equations and math calculations is effectively elucidated to enhance the understanding of young engineering enthusiasts.
Solved example on the Area of Trapezium
Ques 1. Find the area of the trapezium whose length of parallel sides is 2 cm 3 cm and height is 1 cm.
Ans. Given that
a = 2 cm
b = 3 cm
h = 1 cm
Therefore, A= h/2[a + b]
A= 1/2[2 + 3] = 5/2 = 2.5 cm²
Ques 2. Find the area of the trapezium whose length of parallel sides is 6 cm 4 cm and height is 2 cm.
Ans. Given that
a = 6 cm
b = 4 cm
h = 2 cm
Therefore, A= h/2[a + b]
A= 2/2[6 + 4] = 10 = 10 cm²
Ques 3. Find the area of the trapezium whose length of parallel side is 5 cm 7cm and height is 1 cm.
Ans. Given that
a = 5 cm
b = 7 cm
h = 1 cm
Therefore, A= h/2[a + b]
A= 1/2[7 + 5] = 12/2 = 6 cm²
Ques 4. Find the area of the trapezium whose length of parallel sides are 10 cm, 30 cm and height is 4 cm.
Ans. Given that
a = 10 cm
b = 30 cm
h = 4 cm
Therefore, A= h/2[a + b]
A= 4/2[10 + 30] = 2 (40) = 80 cm²
Practice questions for the area of the trapezium
Q1. Find the area of the trapezium whose length of parallel sides is 11cm 33cm and height is 4 cm.
Q2. Find the area of the trapezium whose length of parallel sides is 72 cm 30 cm and height is 6 cm.
Q3. Find the area of the trapezium whose length of parallel sides is 10 cm, 60 cm and height is 9cm.
Q4. Find the area of the trapezium whose length of parallel sides is 16 cm 36 cm and height is 8 cm.








