Table of Contents
Circumference of the Circle: The circumference of the circle is the total length of the boundary of the shape (circle). It is also known as the perimeter of the circle. The circumference of the circle is the product of the diameter of the circle and the constant π, whose value is 3.14 or 22/7.
Circumference of the Circle Meaning
A circle is a 2D, round, and closed figure where all the boundary points are equidistant from the fixed point called the center of the circle. The total length of this Boundary is said to be the Circumference of the Circle.
Examples of the Circumference of the Circle are the fencing around the boundary of a circular park, the border of a circular tabletop, etc. To calculate the length of these discussed examples, we need to calculate the circumference.
Circumference of the Circle Units
The circumference of the circle is always a linear value and its units are the same as the units of length.
Circumference of the Circle Definition
A circle has an area and a perimeter. The perimeter of a circle is also known as the circumference of a circle. This circumference is the distance around the circle. Some of the examples of circles from our daily life are rings, bangles, coins, wheels, buttons, hula-hoop, etc.
If the distance across the border of these examples discussed above is measured properly using the rope, then the total length of the rope covered is called the Circumference of the Circle. Radius is the main component to calculate the circumference of a circle. Therefore, we need the value of radius or the diameter of the circle to calculate the circumference of a circle.
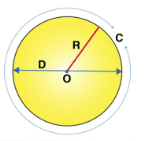
Basic Components of a Circle
- Center of a Circle : There is a center point in a circle. From this point, all the distances to the point on a circle are equal.
- Diameter of a Circle : The diameter of a Circle is a line passing through the center of a circle. Diameter of a circle is the longest chord present in a circle. The diameter is twice the radius of a circle.
- Radius : Radius is the constant distance from the center of a circle to the point present on a circle.
Circumference of the Circle Formula
The Circumference of a Circle is calculated by using the formula: 2πr
where r is the radius of a circle and π is a mathematical constant whose value is 3.14 or 22/7.
Circumference of the Circle Formula Using Diameter
The Circumference of a Circle can be calculated by using the value of the diameter of the circle. The formula to calculate the circumference is:
C=πD
Where C is the circumference of a circle.
D is the diameter of a circle.
The circumference of a circle is measured in units such as cm, m.
Solved Example: Find the circumference of a circle whose radius is 5cm.
Solution: Given radius= 5cm
Therefore, the Circumference of the circle whose radius is 5cm is calculated using the formula = 2πr
= 2×3.14×5
= 31.4cm
How to find the Circumferences of a Circle?
Method 1: The Thread Method
A circle is a curved surface, so the length cannot be measured using a scale or ruler. This method can be used for polygons like squares, rectangles, and triangles. The circumference of a circle can be measured using a thread placed across the circle. The path of a circle can be traced using a thread. On the thread, mark the points. Now, the length can be measured with the help of a ruler.
Method 2: Calculation Using Radius or Diameter
The most accurate way to know the circumference of a circle is to calculate it. To calculate the circumference, the radius of a circle should be known. The radius of a circle is defined as the distance from the center of the circle to any point on the circle itself. Below is the figure in which radius r and center O is shown. The diameter of the circle is twice the radius of the circle.
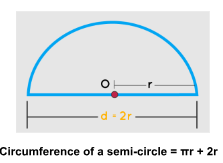
Circumference of the semi-circle
Circumference of the semi-circle is formed when a circle is divided into two equal halves. Therefore, the circumference of a semi-circle also becomes half. But, the length of the diameter of the circle is added to it.
Therefore, the Circumference of a semi-circle = πr + 2r
FAQs on Circumference of Circle
What is the circumference of a circle?
The linear distance around a circle is the circumference of a circle. We can define the circumference of a circle in another way. If we open a circle to form a straight line, the length of that line will be the circumference of a circle.
Find the circumference of a circle whose diameter is given 8cm.
As the diameter of a circle is given, we can find out the radius of a circle. Radius= diameter/2 = 8/2 =4 cm Now, circumference= 2πr = 2×3.14×4 = 25.12 cm
Calculate the radius of a circle whose circumference is C= 25 cm
Circumference = 25 cm C= 2πr 25 = 2×3.14×r r= 25/2×3.14 r= 3.98 cm








