Congruence of Triangles – Different Rules

Congruent figures are two figures that are identical in shape and size. A common example is two bangles of the same size and shape, which would be congruent. In geometry, two objects are considered congruent if they are exactly the same in every measurement. In the case of congruent triangles, we can say that one triangle is an exact copy of the other.

What are Congruent Triangles?

Triangles are three-sided polygons, defined by their three angles, three sides, and three vertices. Based on the lengths of their sides, triangles can be classified as equilateral, isosceles, or scalene. When comparing two different triangles, a different set of rules is applied. Congruent triangles are those that are identical in both side lengths and angle measurements.

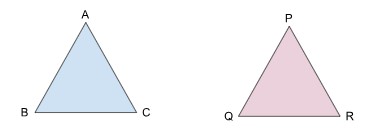
For example in Δ PQR and ΔABC shown below, it is clear that PQ = AB, PR = AC, QR = BC and ∠P = ∠A, ∠Q = ∠B and ∠R = ∠C. Thus we write Δ PQR ≅ ΔABC, i.e. the given triangles are Congruent triangles.

The two triangles need to be of the same size and shape to be Congruent triangles. When we rotate, reflect, and/ or translate a triangle, its position or appearance seems to be different. In that case, we need to identify the six parts of a triangle and their corresponding parts in the other triangle. Consider Δ ABC and ΔPQR as shown below.

Example of Congruent Triangles

• The corresponding vertices are A and P, B and Q, C and R.
• The corresponding sides are AB = PQ, BC = QR, CA = RP.
• The corresponding angles are ∠A = ∠P, ∠B = ∠Q and ∠C = ∠R.

By recognizing the corresponding parts of the triangles in question, one can thus verify that Δ ABC is congruent to ΔPQR.

One Stop Solutions for School Exam Preparation

Boost your school preparation with our comprehensive guide for CBSE, ICSE, and State Board exams. Get all the resources you need in one place and excel in your academic journey. Discover the ultimate one-stop solution at Infinity Learn today!

Conditions of Congruent Triangles

Two triangles are congruent if they have the same size and shape. However, it is not always necessary for both triangles to have all six corresponding elements match exactly. Based on research, there are five conditions that can prove two triangles are congruent:

• SSS (Side-Side-Side)
• SAS (Side-Angle-Side)
• ASA (Angle-Side-Angle)
• AAS (Angle-Angle-Side)
• RHS (Right Angle-Hypotenuse-Side)

SSS Criterion for Congruent triangles

The SSS criterion stands for the Side-Side-Side criterion of triangle congruence. According to this rule, two triangles are congruent if all three sides of one triangle correspond exactly to the three sides of another triangle. This means that if the lengths of the sides of one triangle are equal to the lengths of the sides of another triangle, then the two triangles are congruent.

For example, if ΔABC and ΔDEF have:

1. AB = DE
2. BC = EF
3. CA = FD

Then, by the SSS criterion, ΔABC ≅ ΔDEF. It means that the two triangles are congruent.

Also Check – Equivalent Fractions

SAS Criterion for Congruent triangles

The SAS criterion, or Side-Angle-Side rule, states that two triangles are congruent if two sides and the angle between them in one triangle are equal to the corresponding two sides and the included angle in another triangle. This means that if two triangles share two pairs of equal sides with an equal angle between them, then the triangles are congruent.

For example, if ΔABC and ΔDEF have:

1. AB = DE
2. BC = EF
3. ∠B = ∠E

Then, by the SAS criterion, ΔABC ≅ ΔDEF. This means that the two triangles are congruent.

ASA Criterion for Congruent triangles

The ASA criterion stands for the Angle-Side-Angle criterion. According to this rule, two triangles are said to be congruent if two angles and the side included between them in one triangle are equal to the corresponding angles and included side in another triangle. This ensures that the triangles are congruent in all aspects.

For example, if ΔABC and ΔDEF have:

1. ∠C = ∠F
2. BC = EF
3. ∠B = ∠E

Then, by the ASA criterion, ΔABC ≅ ΔDEF. This means that the two triangles are congruent.

Must Read – Exponents

AAS Criterion for Congruent triangles

The Angle-Angle-Side (AAS) criterion is used to determine if two triangles are congruent. According to this criterion, if two triangles have two angles and one side (which is not between the two angles) equal to the corresponding angles and side of another triangle respectively, then the two triangles are congruent.

For example, if ΔABC and ΔDEF have:

1. ∠C = ∠F
2. ∠B = ∠E
3. AB = DE

Then, by the ASA criterion, ΔABC ≅ ΔDEF. This means that the two triangles are congruent.

The RHS Criterion for Congruent triangles

The Right Angle-Hypotenuse-Side (RHS) criterion is a specific rule for determining the congruence of two right-angled triangles. It is also known as the Hypotenuse-Leg criterion According to this criterion, two right-angled triangles are congruent if:

1. The hypotenuse of one triangle is equal to the hypotenuse of the other.
2. One other side of each triangle is also equal.

Important Notes on Congruent Triangles

Below are a few important points about the congruent triangles.

• Two triangles will be congruent if all three sides and three angles match each other. There are five conditions to determine if two triangles are congruent. These are the criteria of SSS, SAS, ASA, AAS, and RHS.
• A triangle can be a larger replica of another one with same angles hence they may not be congruent in reality. Therefore AAA is not a criterion for determining congruence.
• Congruence is described by the symbol of ≅.
• Two identical triangles have identical perimeters and areas.

Important Notes on Congruent Triangles

Below are a few important points about the congruent triangles.

• Two triangles will be congruent if all three sides and three angles match each other. There are five conditions to determine if two triangles are congruent. These are the criteria of SSS, SAS, ASA, AAS, and RHS.
• A triangle can be a larger replica of another one with same angles hence they may not be congruent in reality. Therefore AAA is not a criterion for determining congruence.
• Congruence is described by the symbol of ≅.
• Two identical triangles have identical perimeters and areas.

Online Mock Test

Boost Your Preparation With Our Free Online Mock Tests For IIT-JEE, NEET And CBSE Exams

Overview of Congruence of Triangles

• The triangle is said to be congruent when its three sides as well as two angles have the same orientation.
• CPCT stands for Corresponding Parts of Congruent Triangles.
• There is a theorem called CPCT theorem which states that two triangles are congruent if they have similar angles and sides, thus their angles are equal and so are their sides.
• When all three sides of the first triangle match with those of the second triangle, then such triangles are said to be congruent as per SSS Rule.
• ASA rule stipulates that if any two angles along with the included side between them is equivalent respectively to corresponding angles and included side between them; then these triangles are said to be congruent.
• In AAS rule, both the angles and the un-included side are equal to the triangle accordingly.
• In RHS rule, hypotenuse and one side of a right-angled triangle are measured equal to one side and hypotenuse of another triangle.
• The perimeters and areas of comparable triangles are similar.
• There is no AAA criteria rule for the congruent rule because one triangle might be an enlarged copy of another triangle even though they might have equal angles.
• Two equilateral triangles might have equal angles but the sides of those triangles might be different hence, there is no congruent triangle in the case of triangles with equilateral triangles.

Congruent Triangles FAQs