Table of Contents
In geometry, a cube is one of the three-dimensional solids. Have you ever seen a Rubik’s Cube? It is an example of a Cube from our daily lives. The Cube has 6 square faces, 8 Vertices and 12 edges. In this article, we will study the Cube, its shape, area, volume, properties and more.
Definition of Cube
As mentioned above, a cube is a three-dimensional shape. It is a geometrical shape with six faces, which are all square. Therefore, all the edges of the cube are equal in length. Below is a picture of the cube and along with that are examples of cubes from our daily life.
Cube Shape in Maths
Cube is one of the three-dimensional solids we study in mathematics. It has 8 Vertices, 12 edges and 6 square-shaped faces. It is also referred to as a Regular Hexahedron.
Sometimes, we refer to the shape of the cube as the ‘cubic shape’. The cube is a platonic solid. It is also referred to as a Square Parallelepiped, a right rhombohedron, or an Equilateral Cuboid. It is considered a convex polyhedron with all the square faces.
Also, the cube has a cubical symmetry. A cube is also considered as a special case of the square prism.
Below given picture is the shape of the Cube:
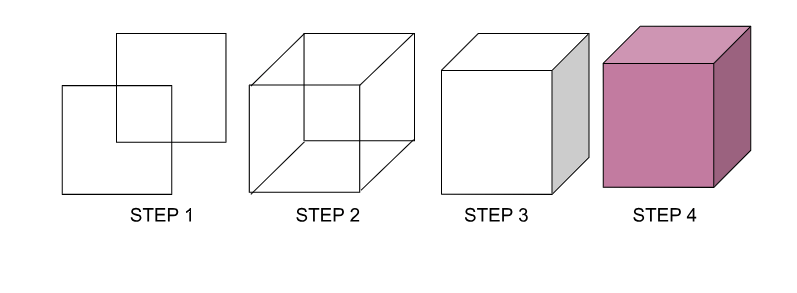
How to Draw a Cube Easily?
Check out the instructions below for drawing a cube easily.
- Draw two squares as shown in step 1 of the picture below.
- Now join the Vertices of both the squares respectively. As given in the figure. (Step 2)
- Now you can rub off the extra lines for better clarity. (Step 3)
- The drawing of a cube is ready. (Step 4)
Cube Shape Examples
There are many examples of cubes in the environment around us. The most common example is of Rubik’s Cube. Also, the eraser we use to erase pencil marks is often in the shape of a cube or cuboid. The packaging boxes made up of cardboard sheets are also in the shape of a cube. Along with that, there are many other examples of cubes around us.
Properties of Cube Shape
A cube is also referred to as a special square prism. It is because all the faces of the cube are square and it is a platonic solid. The properties of the cube are mentioned below.
- A cube has 6 faces, 12 edges and 8 Vertices.
- All the faces of the cube are shaped as squares.
- Therefore, the length, breadth and height of all the faces are equal.
- The angle between any pair of faces is 90°.
- The opposite faces of the cube are parallel to each other.
- Each face of the cube is connected with four other faces through the edges.
- Each of the vertices of the cube meets three edges and three faces.
Cube Net
A cube net is a 2-dimensional representation of a cube. It shows all the three faces of the cube laid down flat on the sheet. These nets can be cut out and can be converted into a three-dimensional cube.
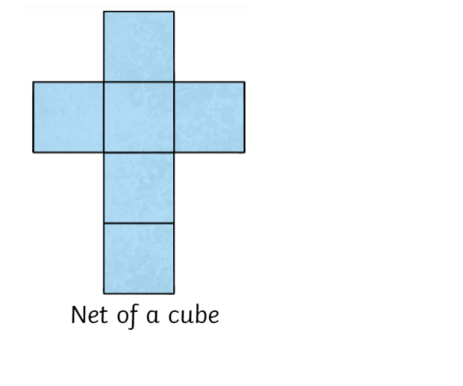
Refer to the picture to get a clear idea about the cube net.
Cube Shape Formulas
As a cube is a solid geometrical shape, therefore, it has surface area and volume. To calculate these easily, we need to use some specific formulas. Below is the list of the formulas popularly used in the case of a cube.
- LSA (Lateral Surface Area) of a Cube = 4a²
- TSA (Total Surface Area) of a Cube = 6a²
- The volume of a Cube = a³
- The diagonal of a face of a Cube = a√2
- Main Diagonal of a Cube = a√3
In all these formulas, a is the length of the edge of the cube.
LSA (Lateral Surface Area) of a Cube
The lateral surface area of a cube is the sum of all the four side faces of the cube. It means that the top face and the base face are not included in the sum.
As we know the area of a single face of the cube will be a² for the edge measuring equal to a unit. Therefore, the total sum of all the four side faces will be equal to 4a².
=> LSA (Lateral Surface Area) of a Cube = 4a²
TSA (Total Surface Area) of a Cube
The total surface area of a cube refers to the total sum of all the faces of the cube. It means that it refers to the sum of all the four side faces along with the top and bottom face of the cube.
As discussed earlier, we know that the area of a single face of the cube will be a² for the edge measuring equal to a unit. Therefore, the total sum of all the six side faces will be equal to 6a².
=> TSA (Total Surface Area) of a Cube = 6a²
Volume of a Cube
The volume of the cube refers to the total area occupied by the cube. In the case of cube shape, the area of the base measured with the height gives us the volume of the geometrical shape, i.e. Cube.
As all the length, breadth and height of the sides of the cube are equal, therefore, the volume of the cube is equal to a³.
Volume of a Cube = (area of the base) × (height of the side)
Volume of a Cube = a² × a
The volume of a Cube = a³
Difference Between a Cube and a Cuboid
The below given table mentions all the major differences between the two geometrical shapes, a Cube and a Cuboid.
| Property | Cube | Cuboid |
| Shape | All the faces of cube are square in shape. | Cuboid has a rectangular shape. All the faces of the cuboid are rectangular in shape. |
| Volume | a³, where a is the measurement of the edge of the face of the cube. | lbh, where l is the length, b is the breadth and h is the height of the shape. |
| Surface Area | 6a² | 2 (lb + bh + hl) |
| Diagonal | a√3 | √(l² + b² + h²) |
| Symmetry | Cube has a rotational symmetry of order 4. | Cuboid has no rational symmetry. |
Solved Problems on Cube Shape
1. What is the volume of water stored in an ice cube with a side length equal to 2 cm?
Ans. Given the length of the side equals 2 cm.
The amount of water stored in an ice cube is equal to the volume of the ice cube.
Therefore, Amount of water stored = 2 × 2 × 2 = 8 cm³
Therefore, the amount of water stored is equal to 8 cm³.
2. Find the TSA (Total Surface Area) of a cube if the length of the side of the cube measures equal to 5 cm.
Ans. The given length of the side of the cube = 5 cm
TSA = 6a²
TSA = 6(5)² = 6 × 25 = 150 cm²
Therefore, the TSA (Total Surface Area) of a cube, if the length of the side of the cube is given as 5 cm, is 150 cm².
Practice Problems on Cube Shape
- What is the volume of sand stored in a cubical box with a side length equal to 7 cm?
- Find the LSA (Lateral Surface Area) of a cube if the length of the side of the cube measures equal to 50 cm.
- Find the TSA (Total Surface Area) of a cube if the length of the side of the cube measures equal to 12 inches.
- What is the volume of pickle that can be stored in a cubical jar with a side length equal to 90 cm?
- Find the LSA (Lateral Surface Area), Volume and TSA (Total Surface Area) of a cube if the length of the side of the cube measures equal to 13 cm.
FAQs on Cube
How to draw 3D cubes?
To draw a 3D cube, start by sketching a square for the front face. Next, draw another square of the same size slightly behind and to the right of the first square. Connect the corresponding corners of both squares with straight lines to create the edges of the cube. To enhance the three-dimensional effect, you can shade one side of the cube darker than the others, indicating a light source, which gives the illusion of depth and volume. Additionally, using perspective techniques, such as foreshortening, can further enhance the realism of your drawing.
Does a cube have 8 face?
A cube does not have 8 faces; rather, it has 6 faces. Each face of a cube is a square, and all faces are congruent, meaning they are identical in shape and size. The confusion may arise from the fact that a cube has 8 vertices (corners) where the edges meet, but it is important to distinguish between faces and vertices in geometric terminology.
What is cube and cuboid?
A cube is a three-dimensional geometric shape with six equal square faces, twelve equal edges, and eight vertices. All angles in a cube are right angles, making it a special case of a cuboid. A cuboid, on the other hand, is a three-dimensional shape that has six rectangular faces, and while all cubes are cuboids, not all cuboids are cubes. Cuboids can have varying lengths, widths, and heights, whereas a cube maintains equal dimensions across all sides.
What is a 3D cube?
A 3D cube is a solid geometric figure that occupies space and has three dimensions: length, width, and height. It is characterized by its six square faces, twelve edges, and eight vertices. The concept of a 3D cube is fundamental in geometry and is often used in various applications, including computer graphics, architecture, and engineering. The cube's uniformity and symmetry make it an essential shape in both theoretical and practical contexts.
Do all cubes have 6 faces?
Yes, all cubes have 6 faces, and each of these faces is a square. The defining characteristic of a cube is that it is a regular polyhedron, specifically a type of hexahedron, where all faces are equal in shape and size. This uniformity in the number of faces, edges, and vertices is what distinguishes cubes from other three-dimensional shapes, ensuring that every cube, regardless of its size, will always maintain this fundamental property.








