Table of Contents
Faces, Edges, and Vertices
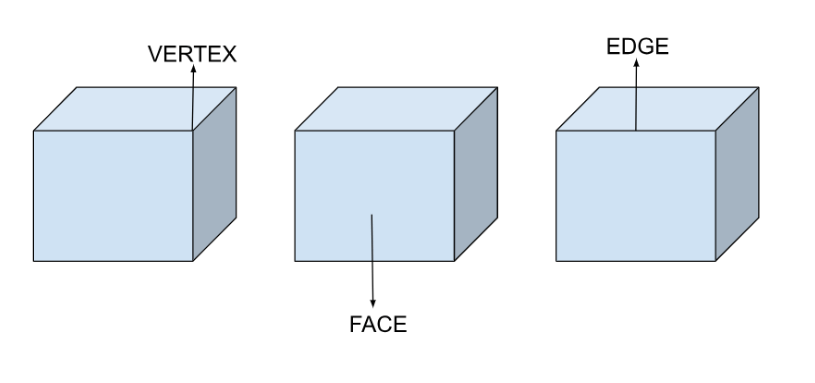
Faces, Edges, and Vertices are the three principal properties that define any 3D solid. The face of an object is the flat surface on it, an edge is a straight line between two faces whereas a vertex is the corner of the shape.
Below are the figures for better clarity about these terms: Faces, Edges, and Vertices.
Faces, Edges, and Vertices Overview
Faces, Edges, and Vertices in math are related to the concept of solids that help us define the 3D object. We come across a number of objects around us that are of different shapes and sizes. They have different types, dimensions, and characteristic properties that set them apart from one another. But despite being different from each other, they all occupy space and are three-dimensional.
The example of objects that have Faces, Edges, and Vertices are ice cubes, books, boxes, chalk, pipe, and more.
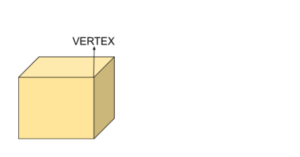
What are Vertices?
In mathematics, a vertex is defined as a point where two or more edges meet. They are also known as the corner points.
The below table gives us the data of the vertices for different shapes.
| Shapes | Number of Vertices |
| Cubes | 8 |
| Cuboids | 8 |
| Cones | 1 |
| Cylinders | No Vertex |
| Spheres | No Vertex |
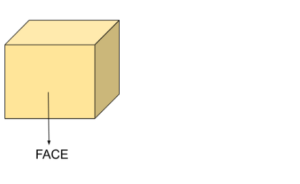
What are Faces?
Every solid has a flat surface. These individual flat surfaces are called Faces. Solids usually have more than one face.
The below table gives us the data of the number of Faces for different shapes.
| Shapes | Number of Faces |
| Cubes | 6 |
| Cuboids | 6 |
| Cones |
|
| Cylinders |
|
| Spheres | Only Curved surfaces |
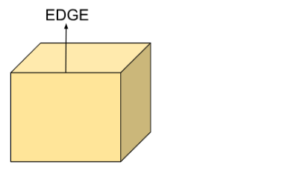
What are Edges?
Edges are defined as a line segment joining two edges.
Definition of Edge: An edge is defined as a line segment that acts as an interface between two faces of a solid.
The below table gives us the data of the number of Edges for different shapes.
| Shapes | Number of Edges |
| Cubes | 12 |
| Cuboids | 12 |
| Cones | 1 |
| Cylinders | 2 |
| Spheres | No Edge |
What are Sides?
Sides is a term generally used for polygons. For example, a Square has four sides while a triangle has 3 sides.
Faces, Edges, and Vertices Formulas
Euler’s formula is used to determine the relation between Faces, Edges, and Vertices. This formula is to be used for closed solids that have flat faces and straight edges such as cubes, cuboids, and more. It can not be used for shapes with curved edges such as cylinders.
Euler’s Formula is given by: F + V – E= 2
Where, F, V, and E are the number of Faces, Vertices, and Edges respectively.
Euler’s Theorem is one of the most important theorems in mathematics. It is named after Leonhard Euler. Euler’s Formula states that for many solid shapes, the number of Edges subtracted from the sum of the number of Faces and number of Vertices gives 2.
Application of Euler’s Formula on Cube
| Shape of the Solid | Cube |
| Vertices | 8 |
| Faces | 6 |
| Edges | 12 |
Let’s apply Euler’s Formula: F + V – E
6 + 8 – 12
= 14 – 12
= 2
Therefore, Eulers Formula is satisfied.
Faces, Edges, and Vertices of 3D Shapes Table
Below given table compares the data of the Faces, Edges, and Vertices of different three-dimensional shapes.
| Shape of the Solid | Vertices | Faces | Edges |
| Cubes | 8 | 6 | 12 |
| Cuboids | 8 | 6 | 12 |
| Cones | 1 | 2 (A Flat Surface and a Curved surface) | 1 |
| Cylinders | 0 (No Vertex) | 3 (2 Flat Surfaces and 1 Curved Surface) | 2 |
| Spheres | 0 (No Vertex) | 1 (Only Curved Surface ) | 0 (No Edge) |
| Shape of the Solid | Vertices | Faces | Edges |
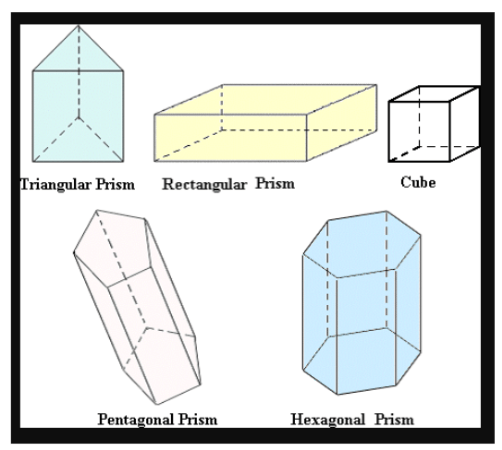
| Triangular Prism | 6 | 5 | 9 |
| Rectangular Prism | 8 | 6 | 12 |
| Square Prism | 8 | 6 | 12 |
| Pentagonal Prism | 10 | 7 | 15 |
| Hexagonal Prism | 12 | 8 | 18 |
| Triangular Pyramid | 4 | 4 | 6 |
| Rectangular Pyramid | 5 | 5 | 8 |
| Square Pyramid | 5 | 5 | 8 |
| Pentagonal Pyramid | 6 | 6 | 10 |
| Hexagonal Pyramid | 7 | 7 | 12 |
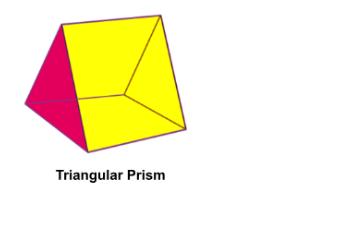
Faces, Edges, and Vertices of Triangular Prism
- A Triangular Prism is made up of 2 triangular bases and 3 rectangular sides.
- It is a three-dimensional shape.
- It has 3 side faces and 2 base faces.
- All these faces are connected by edges.
- Triangular Prism has 5 Faces, 6 Vertices, and 9 Edges.
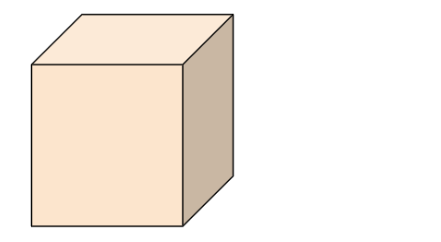
Faces, Edges, and Vertices of Cube
- A Cube is a three-dimensional shape with all sides equal.
- The point at which 3 edges meet is called the Vertex, and each edge connects two vertices.
- A cube has 6 square faces, 12 edges, and 8 vertices.
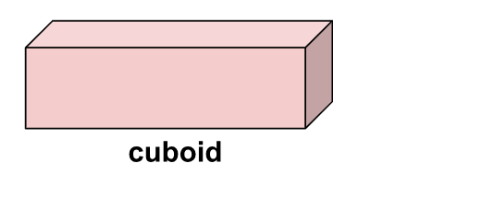
Faces, Edges, and Vertices of Cuboid
- A Cuboid is a three-dimensional shape with rectangular faces.
- The faces of a cuboid are connected by edges.
- Similar to the cube, the vertices are the points where the edges meet.
- It has 6 faces (each face is a rectangle), 12 edges, and 8 vertices.
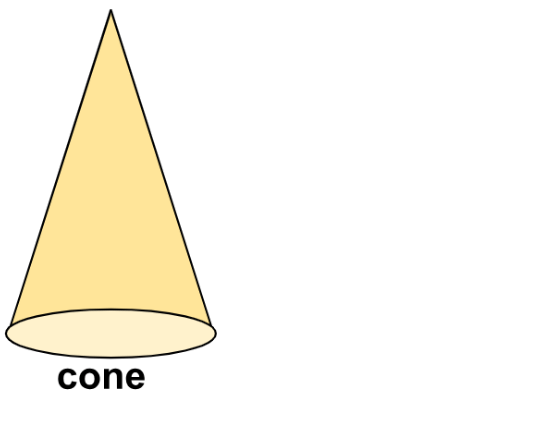
Faces, Edges, and Vertices of Cone
- A Cone is a three-dimensional shape with a circular base and a single curved surface that tapers to a point.
- A cone has 2 faces (1 circular base and 1 curved surface), 1 edge (the circumference of the base), and 1 vertex (the point where the cone tapers).
Faces, Edges, and Vertices of Rectangular Prism
- A Rectangular Prism is a three-dimensional shape with rectangular faces.
- It is similar to a cuboid but can have faces that are not squares.
- It has 6 faces (each face is a rectangle), 12 edges, and 8 vertices.
Also, check, the difference between the Rectangular prism and Cuboid
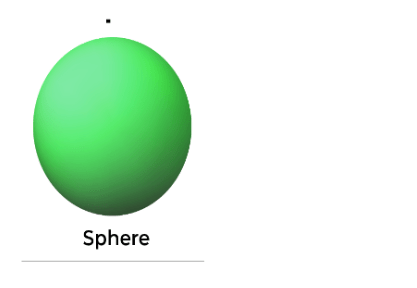
Faces, Edges, and Vertices of Sphere
- A Sphere is a perfectly round three-dimensional shape.
- In a sphere, every point on the surface is equidistant from the center.
- The sphere neither has vertices nor edges.
- The sphere has 1 curved surface.
Faces, Edges, and Vertices of Cylinder
- A Cylinder is a three-dimensional shape with two parallel circular bases connected by a curved surface.
- It has 3 faces, 2 edges (the circular edges of the bases), and 0 vertices.
- The 3 faces of the cylinder include 2 circular bases and 1 curved lateral surface.
- The cylinder has no such points where its edges meet.
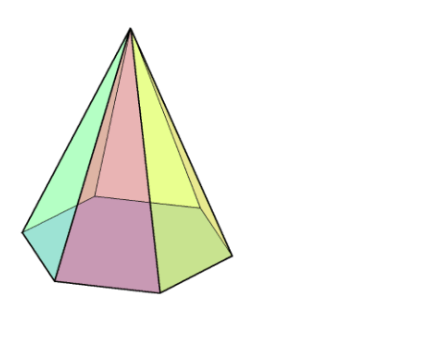
Faces, Edges, and Vertices of Hexagonal Pyramid
- A Hexagonal Pyramid is a three-dimensional shape with a hexagonal base and triangular faces that converge at a single point (the apex).
- It has 7 faces (1 hexagonal base and 6 triangular faces), 12 edges, and 7 vertices (6 vertices on the hexagonal base and 1 at the apex).
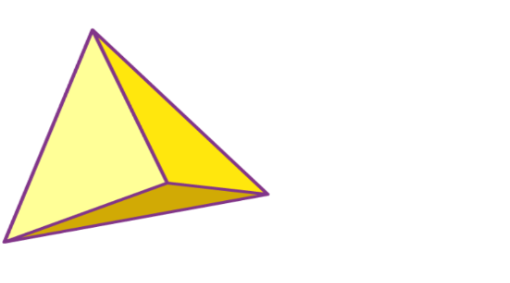
Faces, Edges and Vertices of Triangular Pyramid (Tetrahedron)
- A Triangular Pyramid, also known as a Tetrahedron, is a three-dimensional shape with a triangular base and three triangular faces that converge at a single point (the apex).
- It has 4 faces (all triangles), 6 edges, and 4 vertices.
FAQs on Faces, Edges and Vertices
What are vertices, faces, and edges?
The face of an object is the flat surface on it. An edge is defined as a straight line between two faces whereas a vertex is the corner of the shape. Faces, Edges, and Vertices are the three principle properties that define any 3D solid.
What is Euler’s Formula?
Euler's Formula is given by: F + V - E= 2, where, F, V, and E are the number of Faces, Vertices, and Edges respectively.
What is the difference between 2D and 3D Class 7?
The main difference between 2D and 3D shapes is that 2D shapes have only length and width, while 3D shapes have length, width, and depth. 2D shapes are flat and can be drawn on paper using only the x and y axes, such as squares, circles, and triangles. In contrast, 3D shapes occupy space and can be held in your hand. They require the x, y, and z axes to be represented, and include objects like cubes, spheres, and pyramids. 3D shapes have faces, edges, and vertices, while 2D shapes are simply flat figures with sides and angles. Additionally, 3D shapes give an architectural view of an object, while 2D shapes provide a simple, flat representation
What are 3D shapes class 7?
3D shapes are solid, three-dimensional objects that have length, width, and depth. Some common examples of 3D shapes include: Cube: A cube has 6 square faces, 12 edges, and 8 vertices. Sphere: A sphere is a round, 3D shape like a ball. It has no edges or vertices. Cylinder: A cylinder has 2 circular bases and 1 curved surface, like a can. Pyramid: A pyramid has a polygon base and triangular faces that meet at a single vertex. 3D shapes can be found all around us in everyday objects. Understanding their properties and how they differ from 2D shapes is an important part of geometry.
What is vertices Class 7?
Vertices are the corners or points where the edges of a 3D shape meet. For example, a cube has 8 vertices, one at each corner. Vertices are important features that help define the shape and structure of 3D objects.