Important Questions for Class 10 Maths Chapter 6 Triangles

Understanding triangles is crucial for scoring well in Class 10 Maths. Below, we provide a comprehensive list of important questions for Chapter 6: Triangles. Each question is designed to help students strengthen their understanding of key triangle concepts and formulas.

Important Questions for Class 10 Maths Chapter 6 Key Concepts Covered

• Congruence of Triangles: Understanding the conditions for triangle congruence (SSS, SAS, ASA, RHS).
• Similarity of Triangles: Focus on criteria such as AA, SAS, and SSS for triangle similarity.
• Pythagoras Theorem: Solving real-life and geometric problems using the Pythagoras theorem.

Important Questions for Practice

1. Prove the congruence of two triangles given specific conditions using SSS criterion.
2. Find the missing sides of similar triangles using the properties of proportionality.
3. Apply Pythagoras Theorem to solve practical problems.

Also Check: CBSE Syllabus for Class 10

Important Questions Class 10 Maths Chapter 6 Triangles

Question 1. If ∆ABC ~ ∆PQR, perimeter of ∆ABC = 32 cm, perimeter of ∆PQR = 48 cm and PR = 6 cm, then find the length of AC. (2012)

Solution: ∆ABC ~ ∆PQR …[Given

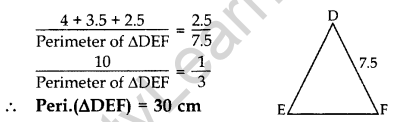
Question 2. ∆ABC ~ ∆DEF. If AB = 4 cm, BC = 3.5 cm, CA = 2.5 cm and DF = 7.5 cm, find the perimeter of ∆DEF. (2012, 2017D)

Solution: ∆ABC – ∆DEF …[Given

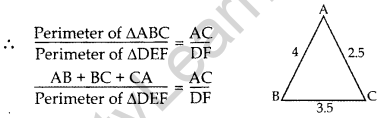
Question 3. If ∆ABC ~ ∆RPQ, AB = 3 cm, BC = 5 cm, AC = 6 cm, RP = 6 cm and PQ = 10, then find QR. (2014)

Solution: ∆ABC ~ ∆RPQ …[Given]

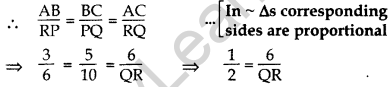
∴ QR = 12 cm

Question 4. In ∆DEW, AB || EW. If AD = 4 cm, DE = 12 cm and DW = 24 cm, then find the value of DB. (2015)

Solution: Let BD = x cm

then BW = (24 – x) cm, AE = 12 – 4 = 8 cm

In ∆DEW, AB || EW

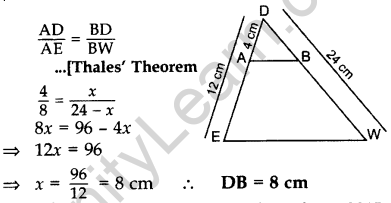
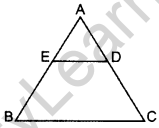
Question 5. In ∆ABC, DE || BC, find the value of x. (2015)

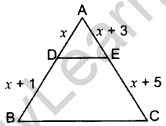
Solution: In ∆ABC, DE || BC …[Given]

x(x + 5) = (x + 3)(x + 1)

x² + 5x = x² + 3x + x + 3

x² + 5x – x² – 3x – x = 3

∴ x = 3 cm

Question 6. In the given figure, if DE || BC, AE = 8 cm, EC = 2 cm and BC = 6 cm, then find DE. (2014)

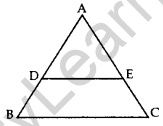
Solution: In ∆ADE and ∆ABC,

∠DAE = ∠BAC …Common

∠ADE – ∠ABC … [Corresponding angles

∆ADE – ∆ΑΒC …[AA corollary

Enroll Now to Online Course for NEET Class 10 Preparation

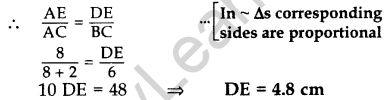
Question 7. In the given figure, XY || QR, \(\frac{P Q}{X Q}=\frac{7}{3}\) and PR = 6.3 cm, find YR. (2017OD)

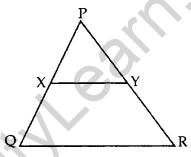
Solution: Let YR = x

\(\frac{\mathrm{PQ}}{\mathrm{XQ}}=\frac{\mathrm{PR}}{\mathrm{YR}}\) … [Thales’ theorem

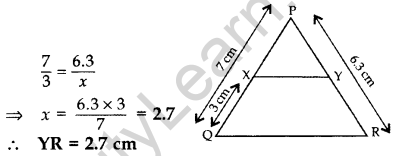
Question 8. The lengths of the diagonals of a rhombus are 24 cm and 32 cm. Calculate the length of the altitude of the rhombus. (2013)

Solution: Diagonals of a rhombus are ⊥ bisectors of each other.

∴ AC ⊥ BD,

OA = OC = \(\frac{A C}{2} \Rightarrow \frac{24}{2}\) = 12 cm

OB = OD = \(\frac{B D}{2} \Rightarrow \frac{32}{2}\) = 16 cm

In rt. ∆BOC,

Question 9. If PQR is an equilateral triangle and PX ⊥ QR, find the value of PX². (2013)

Solution: Altitude of an equilateral ∆,

Important Questions Class 10 Maths Chapter 6 Triangles Short Answer-I (2 Marks)

Question 10. The sides AB and AC and the perimeter P, of ∆ABC are respectively three times the corresponding sides DE and DF and the perimeter P, of ∆DEF. Are the two triangles similar? If yes, find \(\frac { ar\left( \triangle ABC \right) }{ ar\left( \triangle DEF \right) } \) (2012)

Solution:

Given: AB = 3DE and AC = 3DF

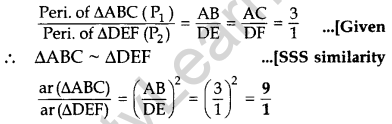
The ratio of the areas of two similar ∆s is equal to the ratio of the squares of their corresponding sides

Question 11. In the figure, EF || AC, BC = 10 cm, AB = 13 cm and EC = 2 cm, find AF. (2014)

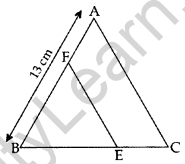
Solution: BE = BC – EC = 10 – 2 = 8 cm

Let AF = x cm, then BF = (13 – x) cm

In ∆ABC, EF || AC … [Given

Question 12. X and Y are points on the sides AB and AC respectively of a triangle ABC such that \(\frac{\mathbf{A X}}{\mathbf{A B}}=\frac{1}{4}\), AY = 2 cm and YC = 6 cm. Find whether XY || BC or not. (2015)

Solution: Given: \(\frac{A X}{A B}=\frac{1}{4}\)

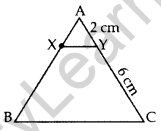
AX = 1K, AB = 4K

∴ BX = AB – AX

= 4K – 1K = 3K

∴ XY || BC … [By converse of Thales’ theorem]

Question 13. In the given figure, ∠A = 90°, AD ⊥ BC. If BD = 2 cm and CD = 8 cm, find AD. (2012; 2017D)

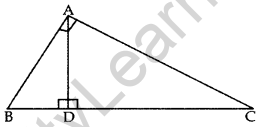
Solution: ∆ADB ~ ∆CDA …[If a perpendicular is drawn from the vertex of the right angle of a rt. ∆ to the hypotenuse then As on both sides of the ⊥ are similar to the whole D and to each other
∴ \(\frac{B D}{A D}=\frac{A D}{C D}\) …[∵ Sides are proportional

AD² = BD , DC

AD² = (2) (8) = 16 ⇒ AD = 4 cm

Question 14. In ∆ABC, ∠BAC = 90° and AD ⊥ BC. Prove that AD\frac{B D}{A D}=\frac{A D}{C D} = BD × DC. (2013)

Solution: In 1t. ∆BDA, ∠1 + ∠5 = 90°

n rt. ∆BAC, ∠1 + ∠4 = 90° …(ii)

∠1 + ∠5 = ∠1 + ∠4 …[From (i) & (ii)

.. ∠5 = ∠4 …(iii)

In ∆BDA and ∆ADC,

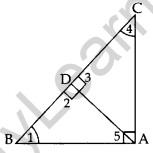
∠5 = 24 … [From (iii)

∠2 = ∠3 …[Each 90°

∴ ∆BDA ~ ∆ADC…[AA similarity

\(\frac{B D}{A D}=\frac{A D}{C D}\)

… [In ~ As corresponding BA sides are proportional

∴ AD² = BD × DC

Question 15. A 6.5 m long ladder is placed against a wall such that its foot is at a distance of 2.5 m from the wall. Find the height of the wall where the top of the ladder touches it. (2015)

Solution: Let AC be the ladder and AB be the wall.

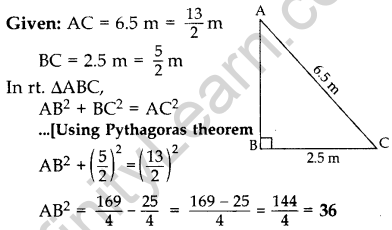
∴Required height, AB = 6 m

Question 16.If in the figure ABC and DBC are two right triangles. Prove that AP × PC = BP × PD. (2013)

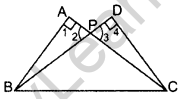
Solution:

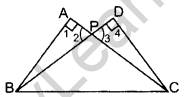
In ∆APB and ∆DPC,

∠1 = ∠4 … [Each = 90°

∠2 = ∠3 …[Vertically opp. ∠s

∴ ∆APB ~ ∆DPC …[AA corollary

⇒ \(\frac{\mathrm{BP}}{\mathrm{PC}}=\frac{\mathrm{AP}}{\mathrm{PD}}\) … [Sides are proportional

∴ AP × PC = BP × PD

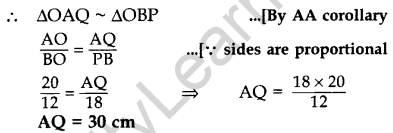
Question 17. In the given figure, QA ⊥ AB and PB ⊥ AB. If AO = 20 cm, BO = 12 cm, PB = 18 cm, find AQuestion (2017OD)

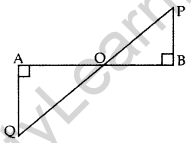
Solution:

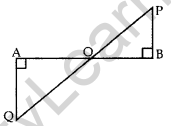
In ∆OAQ and ∆OBP,

∠OAQ = ∠OBP … [Each 90°

∠AOQ = ∠BOP … [vertically opposite angles

Triangles Class 10 Important Questions Short Answer-II (3 Marks)

Question 18. In the given figure, CD || LA and DE || AC. Find the length of CL if BE = 4 cm and EC = 2 cm. (2012)

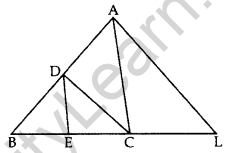
Solution:

In ∆ABL, CD || LA

Question 19. If a line segment intersects sides AB and AC of a ∆ABC at D and E respectively and is parallel to BC, prove that \(\frac{A D}{A B}=\frac{A E}{A C}\). (2013)

Solution: Given. In ∆ABC, DE || BC

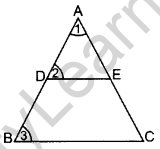
To prove. \(\frac{\mathrm{AD}}{\mathrm{AB}}=\frac{\mathrm{AE}}{\mathrm{AC}}\)

Proof.

In ∆ADE and ∆ABC

∠1 = ∠1 … Common

∠2 = ∠3 … [Corresponding angles

∆ADE ~ ∆ABC …[AA similarity

∴ \(\frac{\mathbf{A D}}{\mathbf{A B}}=\frac{\mathbf{A} \mathbf{E}}{\mathbf{A C}}\)

…[In ~∆s corresponding sides are proportional

Question 20. In a ∆ABC, DE || BC with D on AB and E on AC. If \(\frac{A D}{D B}=\frac{3}{4}\) , find \(\frac{\mathbf{B} C}{\mathbf{D} \mathbf{E}}\). (2013)

Solution:

Given: In a ∆ABC, DE || BC with D on AB and E on AC and \(\frac{A D}{D B}=\frac{3}{4}\)

To find: \(\frac{\mathrm{BC}}{\mathrm{DE}}\)

Proof. Let AD = 3k,

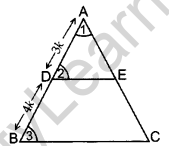
DB = 4k

∴ AB = 3k + 4k = 7k

In ∆ADE and ∆ABC,

∠1 = ∠1 …[Common

∠2 = ∠3 … [Corresponding angles

∴ ∆ADE ~ ∆ABC …[AA similarity

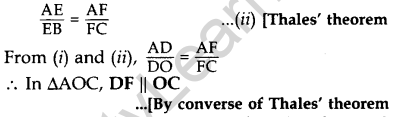
Question 21. In the figure, if DE || OB and EF || BC, then prove that DF || OC. (2014)

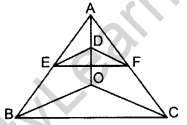
Solution:

Given. In ∆ABC, DE || OB and EF || BC

To prove. DF || OC

Proof. In ∆AOB, DE || OB … [Given

Question 22. If the perimeters of two similar triangles ABC and DEF are 50 cm and 70 cm respectively and one side of ∆ABC = 20 cm, then find the corresponding side of ∆DEF. (2014)

Solution:

Given. ∆ABC ~ ∆DEF,

Perimeter(∆ABC) = 50 cm

Perimeter(∆DEF) = 70 cm

One side of ∆ABC = 20 cm

To Find. Corresponding side of ∆DEF (i.e.,) DE. ∆ABC ~ ∆DEF …[Given

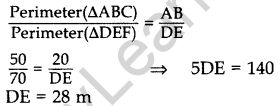
∴ The corresponding side of ADEF = 28 cm

Question 23. A vertical pole of length 8 m casts a shadow 6 cm long on the ground and at the same time a tower casts a shadow 30 m long. Find the height of tower. (2014)

Solution:

Let BC be the pole and EF be the tower Shadow AB = 6 m and DE = 30 m.

In ∆ABC and ∆DEF,

∠2 = ∠4 … [Each 90°

∠1 = ∠3 … [Sun’s angle of elevation at the same time

∆ABC ~ ∆DEF …[AA similarity

\(\frac{A B}{D E}=\frac{B C}{E F}\) … [In -As corresponding sides are proportional

⇒ \(\frac{6}{30}=\frac{8}{\mathrm{EF}}\) ∴ EF = 40 m

Question 24. In given figure, EB ⊥ AC, BG ⊥ AE and CF ⊥ AE (2015)

Prove that:

(a) ∆ABG ~ ∆DCB

(b) \(\frac{\mathbf{B C}}{\mathbf{B D}}=\frac{\mathbf{B E}}{\mathbf{B A}}\)

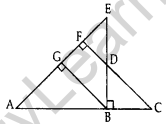
Solution:

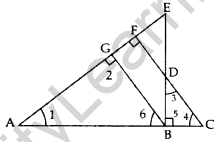
Given: EB ⊥ AC, BG ⊥ AE and CF ⊥ AE.

To prove: (a) ∆ABG – ∆DCB,

(b) \(\frac{B C}{B D}=\frac{B E}{B A}\)

Proof: (a) In ∆ABG and ∆DCB,

∠2 = ∠5 … [each 90°

∠6 = ∠4 … [corresponding angles

∴ ∆ABG ~ ∆DCB … [By AA similarity

(Hence Proved)

∴ ∠1 = ∠3 …(CPCT … [In ~∆s, corresponding angles are equal

(b) In ∆ABE and ∆DBC,

∠1 = ∠3 …(proved above

∠ABE = ∠5 … [each is 90°, EB ⊥ AC (Given)

∆ABE ~ ∆DBC … [By AA similarity

\(\frac{B C}{B D}=\frac{B E}{B A}\)

… [In ~∆s, corresponding sides are proportional

∴ \(\frac{B C}{B D}=\frac{B E}{B A}\) (Hence Proved)

Question 25. ∆ABC ~ ∆PQR. AD is the median to BC and PM is the median to QR. Prove that \(\frac{\mathbf{A B}}{\mathbf{P Q}}=\frac{\mathbf{A D}}{\mathbf{P M}}\). (2017D)

Solution:

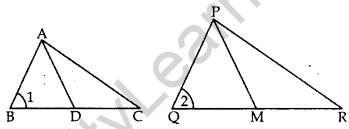
∆ABC ~ ∆PQR … [Given

∠1 = ∠2 … [In ~∆s corresponding angles are equal

Question 26. State whether the given pairs of triangles are similar or not. In case of similarity mention the criterion. (2015)

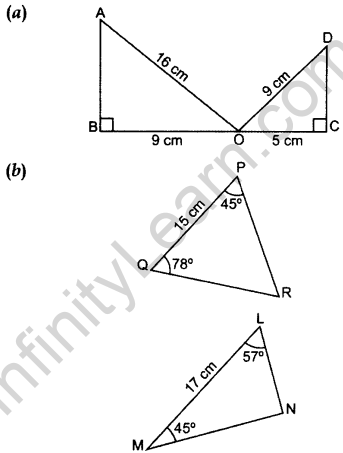
Solution:

(b) In ∆PQR, ∠P + ∠Q + ∠ZR = 180° …[Angle-Sum Property of a ∆

45° + 78° + ∠R = 180°

∠R = 180° – 45° – 78° = 57°

In ∆LMN, ∠L + ∠M + ∠N = 180° …[Angle-Sum Property of a ∆

57° + 45° + ∠N = 180°

∠N = 180° – 57 – 45° = 78°

∠P = ∠M … (each = 45°

∠Q = ∠N … (each = 78°

∠R = ∠L …(each = 57°

∴ ∆PQR – ∆MNL …[By AAA similarity theorem

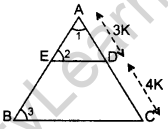
Question 27. In the figure of ∆ABC, D divides CA in the ratio 4 : 3. If DE || BC, then find ar (BCDE) : ar (∆ABC). (2015)

Solution:

Given:

D divides CA in 4 : 3

CD = 4K

DA = 3K

DE || BC …[Given

In ∆AED and ∆ABC,

∠1 = ∠1 …[common

∠2 = ∠3 … corresponding angles

∴ ∆AED – ∆ABC …(AA similarity

⇒ \(\frac { ar\left( \triangle AED \right) }{ ar\left( \triangle ABC \right) } =\left( \frac { AD }{ AC } \right) ^{ 2 }\)

… [The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides

⇒ \(\\frac { \left( 3K \right) ^{ 2 } }{ \left( 7K \right) ^{ 2 } } =\frac { { 9K }^{ 2 } }{ { 49K }^{ 2 } } =\frac { ar\left( \triangle AED \right) }{ ar\left( \triangle ABC \right) } =\frac { 9 }{ 49 } \)

Let ar(∆AED) = 9p

and ar(∆ABC) = 49p

ar(BCDE) = ar (∆ABC) – ar (∆ADE)

= 49p – 9p = 40p

∴ \(\frac { ar\left( BCDE \right) }{ ar\left( \triangle ABC \right) } =\frac { 40p }{ 49p } \)

∴ ar (BCDE) : ar(AABC) = 40 : 49

Question 28. In the given figure, DE || BC and AD : DB = 7 : 5, find \frac { ar\left( \triangle DEF \right) }{ ar\left( \triangle CFB \right) } [/latex] (2017OD)

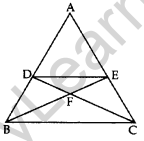
Solution: Given: In ∆ABC, DE || BC and AD : DB = 7 : 5.

To find: \(\frac { ar\left( \triangle DEF \right) }{ ar\left( \triangle CFB \right) } \) = ?

Proof: Let AD = 7k

and BD = 5k then

AB = 7k + 5k = 12k

In ∆ADE and ∆ABC,

∠1 = ∠1 …(Common

∠2 = ∠ABC … [Corresponding angles

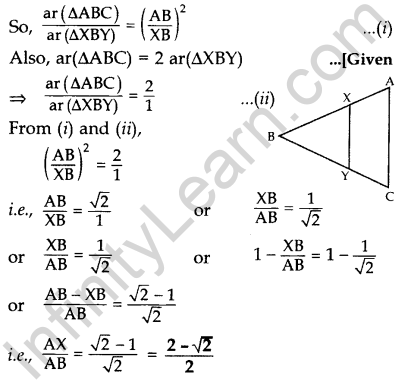
Question 29. In the given figure, the line segment XY is parallel to the side AC of ∆ABC and it divides the triangle into two parts of equal areas. Find the ratio \(\frac{\mathbf{A} \mathbf{X}}{\mathbf{A B}}\). (2017OD)

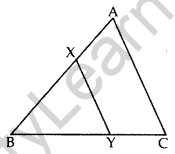
Solution: We have XY || AC … [Given

So, ∠BXY = ∠A and ∠BYX = ∠C …[Corresponding angles

∴ ∆ABC ~ ∆XBY …[AA similarity criterion

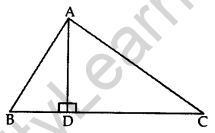
Question 30. In the given figure, AD ⊥ BC and BD = \(\frac{1}{3}\)CD. Prove that 2AC² = 2AB² + BC². (2012)

Solution:

BC = BD + DC = BD + 3BD = 4BD

∴ \(\frac{\mathrm{BC}}{4}\) = BD

In rt. ∆ADB, AD² = AB² – BD² ….(ii)

In rt. ∆ADC, AD² = AC² – CD² …(iii)

From (ii) and (iii), we get

AC² – CD² = AB² – BD²

AC² = AB² – BD² + CD²

∴ 2AC² = 2AB² + BC² (Hence proved)

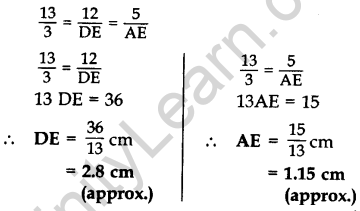
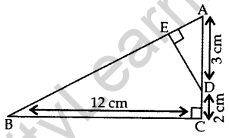
Question 31. In the given figure, ∆ABC is right-angled at C and DE ⊥ AB. Prove that ∆ABC ~ ∆ADE and hence find the lengths of AE and DE. (2012, 2017D)

Solution:

Given: ∆ABC is rt. ∠ed at C and DE ⊥ AB.

AD = 3 cm, DC = 2 cm, BC = 12 cm

To prove:

(i) ∆ABC ~ ∆ADE; (ii) AE = ? and DE = ?

Proof. (i) In ∆ABC and ∆ADE,

∠ACB = ∠AED … [Each 90°

∠BAC = ∠DAE …(Common .

∴ ∆ABC ~ ∆ADE …[AA Similarity Criterion

(ii) ∴ \(\frac{A B}{A D}=\frac{B C}{D E}=\frac{A C}{A E}\) … [side are proportional \(\frac{A B}{3}=\frac{12}{D E}=\frac{3+2}{A E}\)…..[In rt. ∆ACB, … AB² = AC² + BC² (By Pythagoras’ theorem)
= (5)² + (12)² = 169

∴ AB = 13 cm