Table of Contents
The meaning of the word “tangent” is “to touch”. It is similar to the word “tangere” in the Latin language. A tangent refers to the line that touches the circle at only one point on its circumference and does not enter the interior part of the circle. A circle can have an infinite number of tangents. They always make right angles to the radius.
Read the following article to get more information on the tangent, its meaning and theorems.
Tangents meaning
In geometry, a tangent is a line that touches a curve at exactly one point without crossing it to enter the interior of the circle. A tangent can be drawn from an external point to a point on the curve, forming a line that just touches the curve at that single location. One practical example of a tangent is when you ride a bicycle. In this case, every point on the circumference of the wheel touches the ground at a single point, creating a tangent line with the road. This interaction between the wheel and the road is a perfect representation of how tangents work in the real world.
Consider the following figure showing an arc S and a point P located outside the arc. A tangent line is drawn from point P to touch the arc S at a single point.
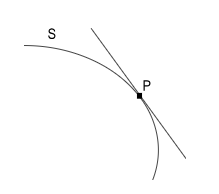
This setup shows us the interaction of a tangent line with a curve.
Tangent definition
In geometry, point tangency is the condition where a line touches some curve or curved surface at one point only. In simpler words, a tangent is a line that touches a curve at exactly one point without crossing it to enter the circle’s interior.
Also Read: Coordinate Geometry
Tangent of a Circle
We know that if a straight line meets or touches the circle at a single point, then it is called a tangent of the circle. A tangent is that line which actually is concurrent with the given circle but does not intersect with it. The diagram given below depicts a circle with a point P marked on it Any line drawn through P that is tangent to the circle is marked as S. Below is an example of a tangent to the circle.
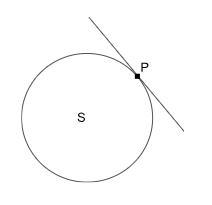
Point of Tangency
The point of tangency is the unique point where a straight line, such as a tangent, touches or intersects a curve without crossing it. It is the exact spot where the curve and the tangent line meet. In the figure given above, point P is highlighted as the point of tangency. This is the specific point where the tangent line just touches the circle, making P the precise point of contact between the line and the circle.
Tangent Properties
The tangent has two important properties
- A tangent line touches a curve, such as a circle, at exactly one point. This unique point is called the point of tangency.
- A tangent line does not cross into the interior of the circle. It only grazes the outer edge.
- At the point of tangency, the tangent line is always perpendicular to the radius of the circle, forming a right angle (90 degrees).
Aside from the above-mentioned properties, a tangent to the circle has mathematical theorems related to it. These theorems are discussed below in detail.
Tangents theorem
Tangents to circles are governed by specific theorems that are crucial in geometric calculations and proofs. These theorems help solve problems involving tangents, circles, and angles. The two most important theorems related to the tangents are discussed below.
- Tangent-Radius Theorem: This theorem states that the tangent to a circle at any given point is perpendicular to the radius drawn to the point of contact.
- Two Tangents Theorem: If two tangents are drawn to a circle from the same external point, they are equal in length. This theorem is often used in proofs and calculations involving circle geometry.
Also Read: Euclidean Geometry
Tangent Radius Theorem
The tangent to a circle at any given point is perpendicular to the radius drawn to the point of contact.
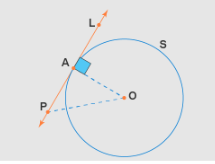
Given: A circle with center O and radius OA. A tangent line PL touches the circle at point A.
To Prove: The tangent PL is perpendicular to the radius OA at the point of contact A.
Proof:
Assume: Point P lies on the line PL, but outside the circle.
Construction: Join P to the center O, forming the line segment PO.
Observation: Since P is outside the circle, the length of PO is greater than the radius OA. Mathematically, PO>OA.
- This condition PO>OA holds true for every point on the line PL except the point A. This is because A is the only point on PL that lies exactly on the circle, making OA the shortest possible distance from the center O to any point on the tangent line PL.
- Since OA is the shortest distance from the center O to the line PL, it implies that OA is the perpendicular distance from O to the tangent line PL.
- By the definition of perpendicularity, the shortest line segment from a point to a line is always perpendicular to that line.
Conclusion: Therefore, OA is perpendicular to the tangent PL at point A.
Hence proved: The tangent at any point of a circle is perpendicular to the radius drawn to the point of contact.
Two Tangents Theorem
If two tangents are drawn to a circle from the same external point, they are equal in length.
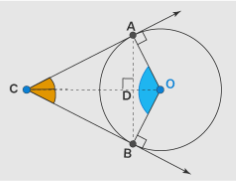
Given: Two tangents CA and CB are drawn to a circle from an exterior point C, touching the circle at points A and B, respectively.
To Prove: The lengths of the two tangents are equal, i.e., CA=CB.
- The two tangents subtend equal angles at the centre of the circle, i.e., ∠COA=∠COB.
- The angle between the tangents is bisected by the line joining the exterior point C to the centre O, i.e., ∠ACO=∠BCO.
Proof:
Construct Triangles: Draw radii OA and OB to the points of tangency A and B. Join OC.
- Identify Key Properties:
- OA=OB (radii of the same circle).
- OC=OC (common side).
Tangent-Radius Perpendicularity:
∠OAC=∠OBC=90° (the tangent to a circle is perpendicular to the radius at the point of tangency).
Triangle Congruence:
In ΔCAO and ΔCBO:
- OA=OB (radii of the circle).
- OC=OC (common side).
- ∠OAC=∠OBC=90° (perpendicularity of tangent and radius).
By the RHS (Right angle-Hypotenuse-Side) criterion, ΔCAO≅ΔCBO.
Conclusions from Congruence:
Since ΔCAO≅ΔCBO, it follows that:
- CA=CB (corresponding sides are equal).
- ∠COA=∠COB (corresponding angles are equal).
- ∠ACO=∠BCO (corresponding angles are equal).
Hence proved: The lengths of the two tangents drawn from an exterior point to a circle are equal, the tangents subtend equal angles at the center, and the angle between the tangents is bisected by the line joining the exterior point to the center.
Tangents of Circles Formula
Now, let’s look into the equation of tangents. Tangent is a line and to write the equation of tangent we need two things, slope (m) and one point on the line.
The general equation of the tangent to a circle is:
- The tangent to a circle equation x² + y² = a² for a line y= mx+c is given by the equation y = mx √ a [ 1 + m2 ]
- The tangent to a circle equation x² + y² =a² at (a1, b1) is xa1 + yb1 = a2
Therefore, the equation of tangent is xa1 + yb1 = a2, where (a1, b1) are coordinates from which it has been drawn.









