Important Questions for Class 10 Maths Chapter 10 Circles

In Chapter 10 of Class 10 Maths, titled “Circles,” several important concepts are explored. One crucial aspect is understanding the properties and theorems related to circles. Key questions might revolve around the relationships between different parts of a circle, such as the radius, diameter, chord, and arc. Theorems like the Inscribed Angle Theorem and the Angle Subtended by an Arc at the Center are fundamental for solving problems related to circles. Additionally, questions on tangents, secants, and their properties within a circle are essential to grasp. To excel in this chapter, students should focus on mastering the theorems, practicing geometric constructions involving circles, and solving numerical problems that test their comprehension of circle-related concepts.

Also Check: CBSE Class 10 Maths Important Question Chapter 8 Tribometry

Class 10 Important Questions Circles – Very Short Answer (1 Mark)

Question 1. In the given figure, O is the centre of a circle, AB is a chord and AT is the tangent at A. If ∠AOB = 100°, then calculate ∠BAT. (2011D)

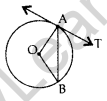
Solution:

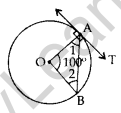
∠1 = ∠2
∠1 + ∠2 + 100° = 180°
∠1 + ∠1 = 80°
⇒ 2∠1 = 80°
⇒ ∠1 = 40°
∠1 + ∠BAT = 90°
∠BAT = 90° – 40° = 50°

Also Check: Important Questions for Class 10 Maths Chapter 14 Statistics

Question 2. In the given figure, PA and PB are tangents to the circle with centre O. If ∠APB = 60°, then calculate ∠OAB, (2011D)

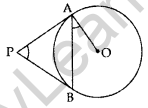
Solution:

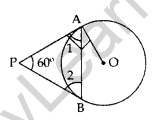
∠1 = ∠2
∠1 + ∠2 + ∠APB = 180°
∠1 + ∠1 + 60° = 180°
2∠1 = 180° – 60° = 120°
∠1 = \(\frac{120^{\circ}}{2}\) = 60°
∠1 + ∠OAB = 90°
60° +∠OAB = 90°
∠OAB = 90° – 60° = 30°

Question 3. In the given figure, O is the centre of a circle, PQ is a chord and PT is the tangent at P. If ∠POQ = 70°, then calculate ∠TPQuestion (2011OD)

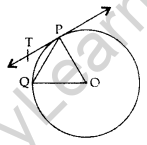
Solution:

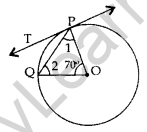
∠1 = ∠2
∠1 + ∠2 + 70° = 180°
∠1 + ∠1 = 180° – 70°
2∠1 = 110° ⇒ ∠1 = 55°
∠1 + ∠TPQ = 90°
55° + ∠TPQ = 90°
⇒ ∠TPQ = 90° – 55° = 35°

Also Check: Surface Areas and Volumes Class 10 Extra Questions Maths Chapter 13

Question 4. A chord of a circle of radius 10 cm subtends a right angle at its centre. Calculate the length of the chord (in cm). (2014OD)
Solution:
AB² = OA² + OB² …[Pythagoras’ theorem

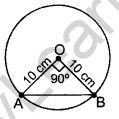
AB² = 10² + 10²
AB² = 2(10)²
AB = \(10 \sqrt{2}\) cm

Question 5.
In the given figure, PQ R is a tangent at a point C to a circle with centre O. If AB is a diameter and ∠CAB = 30°. Find ∠PCA. (2016OD)

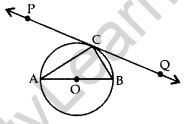
Solution:
∠ACB = 90° …[Angle in the semi-circle
In ∆ABC,
∠CAB + ∠ACB + ∠CBA = 180°
30 + 90° + ∠CBA = 180°
∠CBA = 180° – 30° – 90° = 60°
∠PCA = ∠CBA …[Angle in the alternate segment
∴ ∠PCA = 60°

Also Check: Polynomials Class 10 Extra Questions Maths Chapter 2

Question 6. In the given figure, AB and AC are tangents to the circle with centre o such that ∠BAC = 40°. Then calculate ∠BOC. (2011OD)

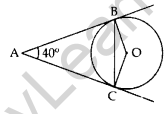
Solution:

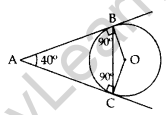
AB and AC are tangents
∴ ∠ABO = ∠ACO = 90°
In ABOC,
∠ABO + ∠ACO + ∠BAC + ∠BOC = 360°
90° + 90° + 40° + ∠BOC = 360°
∠BOC = 360 – 220° = 140°

Question 7. In the given figure, a circle touches the side DF of AEDF at H and touches ED and EF produced at K&M respectively. If EK = 9 cm, calculate the perimeter of AEDF (in cm). (2012D)

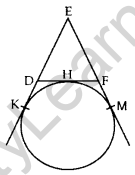
Solution:
Perimeter of ∆EDF
= 2(EK) = 2(9) = 18 cm

Also Check: Some Applications of Trigonometry Class 10 Extra Questions Maths Chapter 9

Question 8. In the given figure, AP, AQ and BC are tangents to the circle. If AB = 5 cm, AC = 6 cm and BC = 4 cm, then calculate the length of AP (in cm). (2012OD)

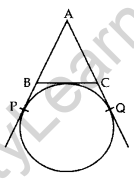
Solution:
2AP = Perimeter of ∆
2AP = 5 + 6 + 4 = 15 cm
AP = \(\frac{15}{2}\) = 7.5 cm

Question 9. In the given figure, PA and PB are two tangents drawn from an external point P to a circle with centre C and radius 4 cm. If PA ⊥ PB, then find the length of each tangent. (2013D)

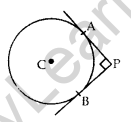
Solution:

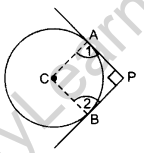
Construction: Join AC and BC.
Proof: ∠1 = ∠2 = 90° ….[Tangent is I to the radius (through the point of contact
∴ APBC is a square.
Length of each tangent
= AP = PB = 4 cm
= AC = radius = 4 cm

Also

Question 10. In the given figure, PQ and PR are two tangents to a circle with centre O. If ∠QPR = 46°, then calculate ∠QOR. (2014D)

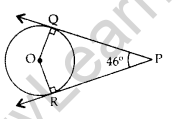
Solution:
∠OQP = 900
∠ORP = 90°
∠OQP + ∠QPR + ∠ORP + ∠QOR = 360° …[Angle sum property of a quad.
90° + 46° + 90° + ∠QOR = 360°
∠QOR = 360° – 90° – 46° – 90° = 134°

Question 11. In the given figure, PA and PB are tangents to the circle with centre O such that ∠APB = 50°. Write the measure of ∠OAB. (2015D)

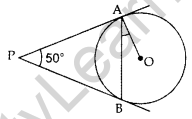
Solution:
PA = PB …[∵ Tangents drawn from external point are equal
∠OAP = ∠OBP = 90°
∠OAB = ∠OBA … [Angles opposite equal sides
∠OAP + ∠AOB + ∠OBP + ∠APB = 360° … [Quadratic rule

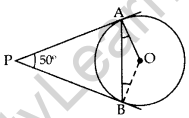
90° + ∠AOB + 90° + 50° = 360°
∠AOB = 360° – 230°
= 130°
∠AOB + ∠OAB + ∠OBA = 180° … [∆ rule
130° + 2∠OAB = 180° … [From (i)
2∠OAB = 50°
⇒ ∠OAB = 25°

Question 12. From an external point P, tangents PA and PB are drawn to a circle with centre 0. If ∠PAB = 50°, then find ∠AOB. (2016D)
Solution:
PA = PB …[∵ Tangents drawn from external point are equal

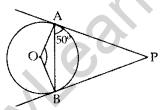
∠PBA = ∠PAB = 50° …[Angles equal to opposite sides
In ∆ABP, ∠PBA + ∠PAB + ∠APB = 180° …[Angle-sum-property of a ∆
50° + 50° + ∠APB = 180°
∠APB = 180° – 50° – 50° = 80°
In cyclic quadrilateral OAPB
∠AOB + ∠APB = 180° ……[Sum of opposite angles of a cyclic (quadrilateral is 180°
∠AOB + 80o = 180°
∠AOB = 180° – 80° = 100°

Question 13. In the given figure, PQ is a chord of a circle with centre O and PT is a tangent. If ∠QPT = 60°, find ∠PRQ. (2015OD)

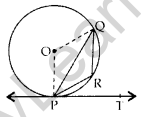
Solution:
PQ is the chord of the circle and PT is tangent.
∴ ∠OPT = 90° …[Tangent is I to the radius through the point of contact
Now ∠QPT = 60° … [Given
∠OPQ = ∠OPT – ∠QPT
⇒ ∠OPQ = 90° – 60° = 30°
In ∆OPQ, OP = OQ
∠OQP = ∠OPQ = 30° … [In a ∆, equal sides have equal ∠s opp. them
Now, ∠OQP + ∠OPQ + ∠POQ = 180°
∴ ∠POQ = 120° …[∠POQ = 180o – (30° + 30°)
⇒ Reflex ∠POQ = 360° – 120° = 240° …[We know that the angle subtended by an arc at the centre of a circle is twice the angle subtended by it at any point on the remaining part of the circle
∴ Reflex ∠POQ = 2∠PRO
⇒ 240° = 2∠PRQ
⇒ ∠PRQ = \(\frac{240^{\circ}}{2}\) = 120°

Question 14. In the given figure, the sides AB, BC and CA of a triangle ABC touch a circle at P, Q and R respectively. If PA = 4 cm, BP = 3 cm and AC = 11 cm, find the length of BC (in cm). (2012D)

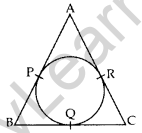
Solution:

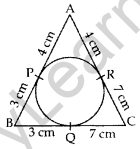
AP = AR = 4 cm
RC = 11 – 4 = 7 cm
RC = QC = 7 cm
BQ = BP = 3 cm
BC = BQ + QC
= 3 + 7 = 10 cm

Question 15. In a right triangle ABC, right-angled at B, BC = 12 cm and AB = 5 cm. Calculate the radius of the circle inscribed in the triangle (in cm). (2014OD)
Solution:

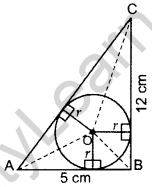
AC² = AB² + BC² …[Pythagoras’ theorem
= (5)² + (12)²
AC² = 25 + 144
AC = \(\sqrt{169}\) = 13 cm
Area of ∆ABC = Area of ∆AOB + ar. of ∆BOC + ar. of ∆AOC

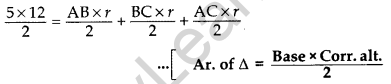
60 = r(AB + BC + AC)
60 = r(5 + 12 + 13)
60 = 30r ⇒ r = 2 cm

Question 16. Find the perimeter (in cm) of a square circum scribing a circle of radius a cm. (2011OD)
Solution:

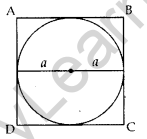
Radius = R
AB = a + a = 2a
∴ Perimeter = 4(AB)
= 4(2a)
= 8a cm

Question 17. In the given figure, a circle is inscribed in a quadrilateral ABCD touching its sides AB, BC, CD and AD at P, Q, R and S respectively. If the radius DA of the circle is 10 cm, BC = 38 cm, PB = 27 cm and AD ⊥ CD, then calculate the length of CD. (2013OD)

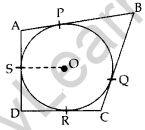
Solution:
Const. Join OR
Proof. ∠1 = ∠2 = 90° … [Tangent is ⊥ to the radius through the point of contact
∠3 = 90° …[Given

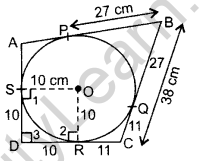
∴ ORDS is a square.
DR = OS = 10 cm …(i)
BP = BQ = 27 cm …[Tangents drawn from an external point
∴ CQ = 38 – 27 = 11 cm
RC = CO = 11 cm …[Tangents drawn from an external point
DC = DR + RC = 10 + 11 = 21 cm …[From (i) & (ii)

Circles Class 10 Important Questions Short Answer-I (2 Marks)

Question 18. Prove that the tangents drawn at the ends of a diameter of a circle are parallel. (2012OD)
Solution:

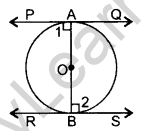
Proof: ∠1 = 90° …(i)
∠2 = 90° …(ii)
∠1 = ∠2 … [From (i) & (ii)
But these are alternate interior angles
∴PQ || RS

Question 19. In the figure, AB is the diameter of a circle with centre O and AT is a tangent. If ∠AOQ = 58°, find ∠ATQ. (2015D)

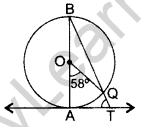
Solution:
∠ABQ = \(\frac{1}{2}\) ∠AOQ = \(\frac{58^{\circ}}{2}\) = 29°
∠BAT = 90° ….[Tangent is ⊥ to the radius through the point of contact
∠ATQ = 180° – (∠ABQ + ∠BAT)
= 180 – (29 + 90) = 180° – 119° = 61°

Question 20. Two concentric circles are of radii 7 cm and r cm respectively, where r > 7. A chord of the larger circle, of length 48 cm, touches the smaller circle. Find the value of r. (2011D)
Solution:

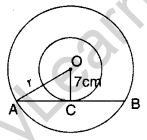
Given: OC = 7 cm, AB = 48 cm
To find: r = ?
∠OCA = 90° ..[Tangent is ⊥ to the radius through the point of contact
∴ OC ⊥ AB
AC = \(\frac{1}{2}\) (AB) … [⊥ from the centre bisects the chord
⇒ AC = \(\frac{1}{2}\) (48) = 24 cm
In rt. ∆OCA, OA² = OC² + AC² … [Pythagoras’ theorem
r² = (7)² + (24)²
= 49 + 576 = 625
∴ r= \(\sqrt{625}\) = 25 cm

Question 21. In the figure, the chord AB of the larger of the two concentric circles, with centre O, touches the smaller circle at C. Prove that AC = CB. (2012D)

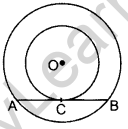
Solution:

Const.: Join OC
Proof: AB is a tangent to smaller circle and OC is a radius.
∴ ∠OCB = 90° … above theorem
In the larger circle, AB is a chord and OC ⊥ AB.
∴ AC = CB … [⊥ from the centre bisects the chord

Question 22. In the given figure, a circle touches all the four sides of a quadrilateral ABCD whose sides are AB = 6 cm, BC = 9 cm and CD = 8 cm. Find the length of side AD. (2011OD)

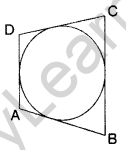
Solution:
AB + CD = AD + BC
6 + 8 = AD + 9
14 – 9 = AD ⇒ AD = 5 cm

Question 23. Prove that the parallelogram circumscribing a circle is a rhombus. (2012D, 2013D)
Solution:
Given. ABCD is a ॥^gm.
To prove. ABCD is a rhombus.
Proof. In ॥^gm, opposite sides are equal

AB = CD
and AD = BC ..(i)
AP = AS …[Tangents drawn from an external point are equal in length
PB = BQ
CR = CO
DR = DS
By adding these tangents,
(AP + PB) + (CR + DR) = AS + BQ + CQ + DS
AB + CD = (AS + DS) + (BQ + CQ)
AB + CD = AD + BC
AB + AB = BC + BC … [From (i)
2AB = 2 BC
AB = BC …(ii)
From (i) and (ii), AB = BC = CD = DA
∴ ॥^gm ABCD is a rhombus.

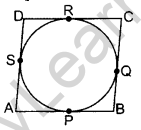
Question 24. In figure, a quadrilateral ABCD is drawn to circum- DA scribe a circle, with centre O, in such a way that the sides AB, BC, CD and DA touch the circle at the points P, Q, RA and S respectively. Prove that: AB + CD = BC + DA. (2013 OD, 2016 OD)

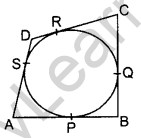
Solution:

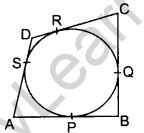
AP = AS ……(i) (Tangents drawn from an external point are equal in length
BP = BO …(ii)
CR = CQ ….(iii)
DR = DS ..(iv)
By adding (i) to (iv)
(AP + BP) + (CR + DR) = AS + BQ + CQ + DS
AB + CD = (BQ + CQ) + (AS + DS)
∴ AB + CD = BC + AD (Hence proved)

Question 25. In the given figure, an isosceles ∆ABC, with AB = AC, circumscribes a circle. Prove that the point of contact P bisects the base BC. (2012D)

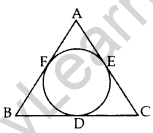
Solution:
Given: The incircle of ∆ABC touches the sides BC, CA and AB at D, E and F F respectively.

AB = AC
To prove: BD = CD
Proof: Since the lengths of tangents drawn from an external point to a circle are equal
∴ AF = AE … (i)
BF = BD …(ii)
CD = CE …(iii)
Adding (i), (ii) and (iii), we get
AF + BF + CD = AE + BD + CE
⇒ AB + CD = AC + BD
But AB = AC … [Given
∴ CD = BD

Question 26. In Figure, a right triangle ABC, circumscribes a circle of radius r. If AB and BC are of lengths 8 cm and 6 cm respectively, find the value of r. (2012OD)

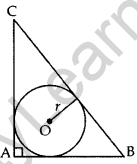
Solution:
Const.: Join AO, OB, CO
Proof: area of ∆ABC

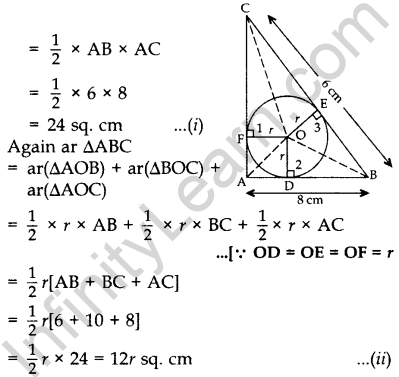
From (i) and (ii), we get 12r = 24
∴ r = 2 cm

Question 27. In the given figure, a circle inscribed in ∆ABC touches its sides AB, BC and AC at points D, E & F K respectively. If AB = 12 cm, BC = 8 cm and AC = 10 cm, then find the lengths of AD, BE and CF. (2013D)

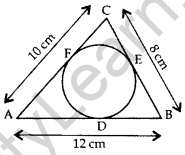
Solution:
Let AD = AF = x
BD = BE = y …[Two tangents drawn from and an external point are equal
CE = CF = z

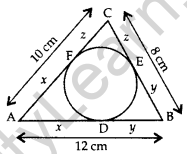
AB = 12 cm …[Given
∴ x + y = 12 cm …(i)
Similarly,
y + z = 8 cm …(ii)
and x + z = 10 cm …(iii)
By adding (i), (ii) & (iii)
2(x + y + z) = 30
x + y + z = 15 …[∵ x + y = 12
z = 15 – 12 = 3
Putting the value of z in (ii) & (iii),
y + 3 = 8
y = 8 – 3 = 5
x + 3 = 10
x = 10 – 3 = 7
∴ AD = 7 cm, BE = 5 cm, CF = 3 cm

Question 28. The incircle of an isosceles triangle ABC, in which AB = AC, touches the sides BC, CA and AB at D, E and F respectively. Prove that BD = DC. (2014OD)
Solution:
Given: The incircle of ∆ABC touches the sides BC, CA and AB at D, E and F respectively.

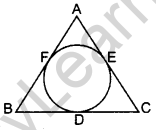
AB = AC
To prove: BD = CD
Proof: AF = AE ..(i)
BF = BD …(ii)
CD = CE …(iii)
Adding (i), (ii) and (iii), we get
AF + BF + CD = AE + BD + CE
⇒ AB + CD = AC + BD
But AB = AC …[Given
∴ CD = BD

Question 29. In the figure, a ∆ABC is drawn to circumscribe a circle of radius 3 cm, such that the segments BD and DC are respectively 6 cm 9 cm of lengths 6 cm and 9 cm. If the area of ∆ABC is 54 cm², then find the lengths of sides AB and AC. (2011D, 2011OD, 2015 OD)

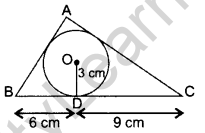
Solution:
Given: OD = 3 cm; OE = 3 cm; OF = 3 cm ar(∆ABC) = 54 cm²

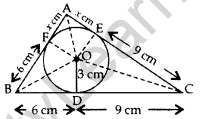
Joint: OA, OF, OE, OB and OC
Let AF = AE = x
BD = BF = 6 cm
CD = CE = 9 cm
∴ AB = AF + BF = x + 6 …(i)
AC = AE + CE = x + 9 …(ii)
BC = DB + CD = 6 + 9 = 15 cm …(iii)
In ∆ABC,
Area of ∆ABC = 54 cm² …[Given
ar(∆ABC) = ar(∆BOC) + ar(∆AOC) + ar(∆AOB)

Question 30. In the figure, a circle is inscribed in a ∆ABC, such that it touches the sides AB, BC and CA at points D, E and F respectively. If the lengths of sides AB, BC, and CA are 12 cm, 8 cm and 10 cm respectively, find the lengths of AD, BE and CF. (2016D)

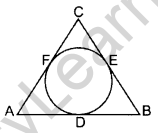
Solution:
AB = 12 cm, BC = 8 cm, CA = 10 cm

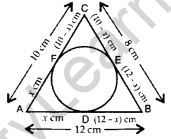
As we know,
AF = AD
CF = CE
BD = BE
Let AD = AF = x cm
then, DB = AB – AD
= (12 – x) cm
∴ BE = (12 – x) cm ..[Tangents drawn from an external point are equal
Similarly,
CF = CE = AC – AF = (10 – x) cm
BC = 8 cm …[Given
⇒ BE + CE = 8 ⇒ 12 – x + 10 – x = 8
⇒ 22 – 8 = 2x ⇒ 2x = 14
∴ x = 7 ∴ AD = x = 7 cm
BE = 12 – x = 12 – 7 = 5 cm
CF = 10 – x = 10 – 7 = 3 cm

Question 31. In Figure, common tangents AB and CD to the two circles with lo, centres O₁ and O₂ intersect at E. Prove that AB = CD. (2014OD)

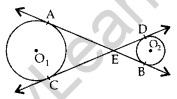
Solution:
EA = EC …(i) ….[Tangents drawn from an external point are equal
EB = ED …(ii)
EA + EB = EC + ED …[Adding (i) & (ii)
∴ AB = CD (Hence proved)

Question 32. If from an external point P of a circle with centre O, two tangents PQ and PR are drawn such that ∠QPR = 120°, prove that 2PQ = PO. (2014D)
Solution:
∠OPQ = \(\frac{1}{2}\)(∠QPR) ..[Tangents drawn from an external point are equal
= \(\frac{1}{2}\)(120°) = 60° …[Tangent is ⊥ to the radius through the point of contact
∠OQP = 90°
In rt. ∆OQP, cos 60° = \(\frac{PQ}{PO}\)
\(\frac{1}{2}=\frac{P Q}{P O}\) ∴ 2PQ = PO

Question 33. From a point T outside a circle of centre O, tangents TP and TQ are drawn to the circle. Prove that OT is the right bisector of line segment PQuestion (2015D)
Solution:
In ∆s’ TPC and TQC ….[Tangents drawn from an external point are equal
TP = TQ
TC = TC …[Common
∠1 = ∠2 …[TP and TQ are equally inclined to OT
∴ ∆TPC = ∆TQC … [SAS
∴ PC = QC …[CPCT

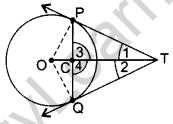
∠3 = ∠4 …(i)
⇒ ∠3 + 24 = 180° … [Linear pair
⇒ ∠3 + ∠3 = 180°…[From (i)
⇒ 2∠3 = 180° ⇒ ∠3 = 90°
∴ ∠3 = ∠4 = 90°
∴ OT is the right bisector of PQuestion

Question 34. In the figure, two tangents RQ and RP are drawn from an external point R to the circle with centre O. If ∠PRQ = 120°, then prove that OR = PR + R. (2015OD)

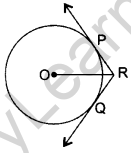
Solution:
Join OP and OO
∠OPR = 90°
PR = RQ … [Tangents drawn from an external point are equal
∠PRO = \(\frac{1}{2}\) ∠PRQ = \(\frac{1}{2}\) × 120° = 60°
Now, In ∆OPR,

⇒ ∠OPR + ∠POR + ∠ORP = 180° …[∆ Rule
⇒ 90° + ∠POR + 60° = 180°
⇒ ∠POR + 150° = 180°
⇒ ∠POR = 30°
⇒ sin 30° = \(\frac{PR}{OR}\) ⇒ \(\frac{1}{2}=\frac{P R}{O R}\)
⇒ OR = 2PR
⇒ OR = PR + QR (∵ PR = RQ) …(Hence proved)

Question 35. In the figure, AP and BP are tangents to a circle with centre 0, such that AP = 5 cm and ∠APB = 60°. Find the length of chord AB. (2016D)

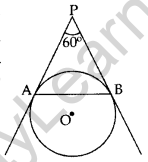
Solution:
PA = PB …[Tangents drawn from an external point are equal
Given:
∠APB = 60°
∠PAB = ∠PBA … (i) …(Angles opposite to equal sides
In ∆PAB, ∠PAB + ∠PBA + ∠APB = 180° …[Angle-sum-property of a ∆
⇒ ∠PAB + ∠PAB + 60° = 180°
⇒ 2∠PAB = 180° – 60o = 120°
⇒ ∠PAB = 60°
⇒ ∠PAB = ∠PBA = ∠APB = 60°
∴ APAB is an equilateral triangle
Hence, AB = AP = 5 cm …[∵ All sides of an equilateral A are equal

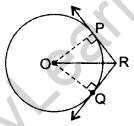
Question 36. In the figure, from an external point P, two tangents PT and PS are drawn to a circle with centre O and radius r. If OP = 2r, show that ∠OTS = ∠OST = 30°. (2016OD)

Solution:
Let ∠TOP = θ …[Tangent is ⊥ to the radius through the point of contact
∠OTP = 90°
OT = OS = r … [Given
In rt. ∆OTP, cos θ = \(\frac{\mathrm{OT}}{\mathrm{OP}}\)
⇒ cos θ = \(\frac{r}{2 r}\) ⇒ cos θ = \(\frac{1}{2}\)
⇒ cos θ = cos 60° ⇒ θ = 60°
∴ ∠TOS = 60° + 60° = 120°
In ATOS,
∠OTS = ∠OST …[Angles opposite to equal sides
In ∠TOS,
∠TOS + ∠OTS + ∠OST = 180° … [Angle-sum-property of a ∆
120° + ∠OTS + ∠OTS = 180° … [From (i)
2∠OTS = 180° – 120°
∠OTS = 60°/2 = 30°
∴ ∠OTS = ∠OST = 30°

Question 37. In the given figure, PA and PB are tangents to the circle from an external point P. CD is another tangent touching the circle at Question If PA = 12 cm, QC = QD = 3 cm, then find PC + PD. (2017D)

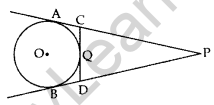
Solution:

PA = PB = 12 cm …(i)
QC = AC = 3 cm …(ii)
QD = BD = 3 cm …(iii)
To find: PC + PD
= (PA – AC) + (PB – BD)
= (12 – 3) + (12 – 3) … [From (i), (ii) & (iii)
= 9 + 9 = 18 cm

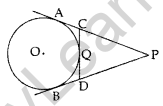
Question 38. In the figure, two circles touch each other at the point C. Prove that the common tangent to the circles at C, bisects the common tangent at P and Q. (2013 OD)

Solution:
To prove: PR = RQ
Proof: PR = RC … (i)
QR = RC
From (i) and (ii), PR = QR (Hence proved)

Circles Class 10 Important Questions Short Answer-II (3 Marks)

Question 39. In the figure, a circle is inscribed in a triangle PQR with PQ = 10 cm, QR = 8 cm and PR = 12 cm. Find the lengths of QM, RN and PI. (2012OD)

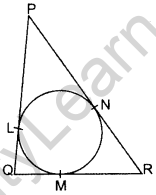
Solution:
Let PL = PN = x cm
QL = QM = y cm
RN = MR = z cm
PQ = 10 cm = x + y = 10 …(i)
QR = 8 cm = y + z = 8 …(ii)
PR = 12 cm = x + z = 12 …(iii)
By adding (i), (ii) and (iii),

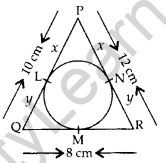
We get,
⇒ 2x + 2y + 2z = 10 + 8 + 12
⇒ 2(x + y + z) = 30
⇒ x + y + z = 15
⇒ 10 + z = 15 … [From (i)
∴ z = 15 – 10 = 5 cm
From (ii)
y + 5 = 8
y = 8 – 5
y = 3 cm
From (iii)
x + 5 = 12
x = 12 – 5
x = 7 cm
∴ QM = 3 cm, RN = 5 cm, PL = 7 cm

Question 40. Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle. (2012D)
Solution:
1st method:
To prove. (i) ∠AOD + ∠BOC = 180°
(ii) ∠AOB + ∠COD = 180°
Proof. In ∆BPO and ∆BQO …[Tangents drawn from an external point are equal

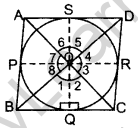
PO = 20 … [radii
BO = BO … [Common
∆BPO = ∆BQO … [SSS Congruency rule
∠8 = ∠1 …(i) (c.p.c.t.)
Similarly,
∠2 = ∠3, ∠4 = ∠5 and ∠6 = ∠7
∠1 + ∠2 + 23+ 24 + 25 + 26+ 27 + ∠8 = 360° …(Complete angles
∠1 + ∠2 + 22+ 25 + 25 + 26+ ∠6+ ∠1 = 360°
2(∠1 + ∠2 + 25 + 26) = 360°
∠BOC + ∠AOD = 180°…(i) [Proved part I
∠AOB + ∠BOC + ∠COD + ∠DOA = 360° …(Complete angles
∠AOB + ∠COD + 180o = 360° … [From (i)
∴ ∠AOB + ∠COD = 360° – 180o = 180° …(proved)

2nd method:
To prove:
(i) ∠6 + ∠8 = 180°
(ii) ∠5 + ∠7 = 180°
Proof. As AS and AP are tangents to the circle from a point A
∴ O lies on the bisector of ∠SAP
∴ ∠1 = \(\frac{1}{2}\) ∠BAD …(i)
Similarly BO, CO and DO are the bisectors of
∠ABC, ∠BCD and ∠ADC respectively. …(ii)

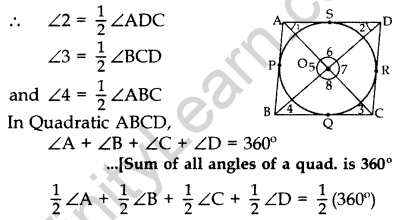
∴ ∠1 + ∠4 + ∠3 + ∠2 =180°…(iii) ..[From (1) & (ii)
In ∆AOD, ∠1 + ∠2 + 26 = 180° …[Angle-sum-Prop. of a ∆
In ∆BOC, ∠3 + ∠4 + ∠8 = 180° …(v)
Adding (iv) and (v)
(∠1 + ∠2 + 23 + 24) + 26 + 28 = 180° + 180°
180° + 26 + 28 = 180° + 180° … [From (iii)
∴∠6 + 28 = 180°
Now ∠5 + ∠6 + ∠7 + ∠8 = 360° … (Complete angles
(∠5 + ∠7) + (∠6 + ∠8) = 360°
(∠5 + ∠7) + 180° = 360°
∠5 + ∠7 = 360° – 180° = 180°
∠5 + ∠7 = 180°

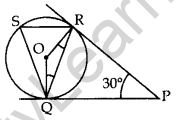
Question 41. Two tangents TP and TQ are drawn to a circle with centre O from an external point T. Prove that ∠PTQ = 2∠OPQ. (2017D)
Solution:
We are given a circle with centre O, an external point T and two tangents TP and TQ to the circle, where P, Q are the points of contact (see Figure).

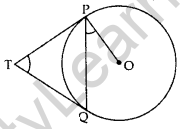
We need to prove that:
∠PTQ = 2∠OPQ
Let ∠PTQ = θ
Now, TP = TQuestion ….[∵ Lengths of tangents drawn from an external pt. to a circle are equal
So, TPQ is an isosceles triangle.

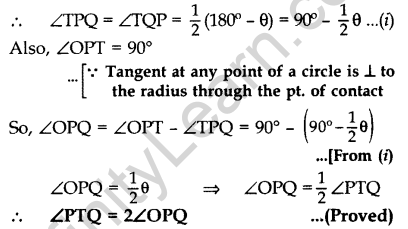
Circles Class 10 Important Questions Long Answer (4 Marks)

Question 42. Prove that the tangent at any point of a circle is perpendicular to the radius through the point of contact. (2011OD, 2012OD, 2013D, 2014OD, 2015D)
Solution:

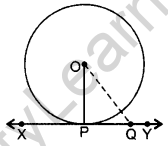
Given: XY is a tangent at point P to the circle with centre O.
To prove: OP ⊥ XY
Const.: Take a point Q on XY other than P and join to OQuestion
Proof: If point Q lies inside the circle, then XY will become a secant and not a tangent to the circle.
∴ OQ > OP
This happens with every point on the line XY except the point P.
OP is the shortest of all the distances of the point O to the points of XY
∴ OP ⊥ XY … [Shortest side is ⊥

Question 43.
Prove that the lengths of tangents drawn from an external point to a circle are equal. (2011D, 2012OD, 2013OD, 2014, 2015D & OD
2016D & OD, 2017D)
Solution:
Given: PT and PS are tangents from an external point P to the circle with centre O.

To prove: PT = PS
Const.: Join O to P,
T & S
Proof: In ∆OTP and
∆OSP,
OT = OS …[radii of same circle
OP = OP …[circle
∠OTP – ∠OSP …[Each 90°
∴ AOTP = AOSP …[R.H.S
PT = PS …[c.p.c.t

Question 44.

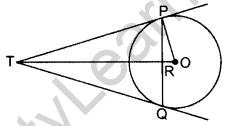
In the above figure, PQ is a chord of length 16 cm, of a circle of radius 10 cm. The tangents at P and Q intersect at a point T. Find the length of TP. (2014OD)
Solution:
TP = TQuestion .. [Tangents drawn from an external point
∆TPQ is an isosceles ∆ and TO is the bisector of ∠PTQ ,
OT ⊥ PQ …[Tangent is ⊥ to the radius through the point of contact
∴ OT bisects PQ
∴ PR = RQ = 16 = 8 cm …[Given
In rt. ∆PRO,
PR² + RO² = PO² … [Pythagoras’ theorem
8² + RO² = (10)²
RO² = 100 – 64 = 36
∴ RO = 6 cm
Let TP = x cm and TR = y cm
Then OT = (y + 6) cm
In rt. ∆PRT, x² = y² + 8² …(i) …[Pythagoras’ theorem
In rt. ∆OPT,
OT² = TP² + PO² …(Pythagoras’ theorem
(y + 6)² = x² + 10²
y² + 12y + 36 = y² +64 + 100 …[From (i)
12y = 164 – 36 = 128 ⇒ y = \(\frac{128}{12}=\frac{32}{3}\)
Putting the value of y in (i),

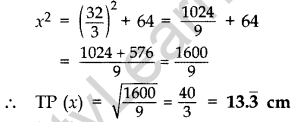
Question 45. In the figure, tangents PQ and PR are drawn from an external point P to a circle with centre O, such that ∠RPQ = 30°. A chord RS is drawn parallel to the tangent PQuestion Find ∠RQS. (2015D)

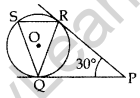
Solution:
PR = PO …[∵ Tangents drawn from an external point are equal
⇒ ∠PRQ = ∠PQR …[∵ Angles opposite equal sides are equal
In ∆PQR,

⇒ ∠PRQ + ∠RPQ + ∠POR = 180°…[∆ Rule
⇒ 30° + 2∠PQR = 180°
⇒ \(\angle \mathrm{PQR}=\frac{(180-30)^{\circ}}{2}\)
= 75°
⇒ SR || QP and QR is a transversal
∵ ∠SRQ = ∠PQR … [Alternate interior angle
∴ ∠SRO = 75° …..[Tangent is I to the radius through the point of contact
⇒ ∠ORP = 90°
∴ ∠ORP = ∠ORQ + ∠QRP
90° = ∠ORQ + 75°
∠ORQ = 90° – 75o = 150
Similarly, ∠RQO = 15°
In ∆QOR,
∠QOR + ∠QRO + ∠OQR = 180° …[∆ Rule
∴∠QOR + 15° + 15° = 180°
∠QOR = 180° – 30° = 150°
⇒ ∠QSR = \(\frac{1}{2}\)∠QOR
⇒ ∠QSR = \(\frac{150^{\circ}}{2}\) = 750 … [Used ∠SRQ = 75° as solved above
In ARSQ, ∠RSQ + ∠QRS + ∠RQS = 180° … [∆ Rule
∴ 75° + 75° + ∠RQS = 180°
∠RQS = 180° – 150o = 30°

Question 46. Prove that the tangent drawn at the mid-point of an arc of a circle is parallel to the chord joining the end points of the arc. (2015OD)
Solution:

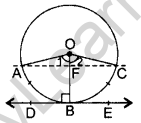
B is the mid point of arc (ABC)
OA = OC …[Radius
OF = OF …[Common
∴ ∠1 = ∠2 …[Equal angles opposite equal sides
∴ ∆OAF = ∆OCF (SAS)
∴ ∠AFO = ∠CFO = 90° …[c.p.c.t
⇒ ∠AFO = ∠DBO = 90° …[Tangent is ⊥to the radius through the point of contact
But these are corresponding angles,
∴ AC || DE

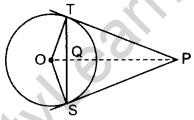
Question 47. In the figure, O is the centre of a circle of radius 5 cm. T is a point such that OT = 13 cm and OT intersects circle at E. If AB is a tangent to the circle at E, find the length of AB, where TP and TQ are two tangents to the circle. (2016D)

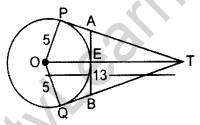
Solution:
∠OPT = 90° …[Tangent is ⊥ to the radius through the point of contact
We have, OP = 5 cm, OT = 13 cm
In rt. ∆OPT,
OP² + PT² = OT? …[Pythagoras’ theorem
⇒ (5)² + PT² = (13)²
⇒ PT² = 169 – 25 = 144 cm
⇒ PT = \(\sqrt{144}\)
= 12 cm
OP = OQ = OE = 5 cm … [Radius of the circle
ET = OT – OE
= 13 – 5 = 8 cm
Let, PA = x cm, then AT = (12 – x) cm
PA = AE = x cm …[Tangent drawn from an external point
In rt. ∆AET,
AE² + ET² = AT² …(Pythagoras’ theorem
⇒ x² + (8)² = (12 – x)²
⇒ x² + 64 = 144 + x² – 24x
⇒ 24x = 144 – 64
x = \(\frac{80}{24}=\frac{10}{3}\) cm
AB = AE + EB = AE + AE = 2AE = 2x :
∴ AB = \(2\left(\frac{10}{3}\right)=\frac{20}{3} \mathrm{cm}=6 \frac{2}{3}\) cm
or 6.67 cm or 6.6 cm

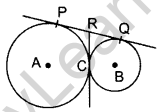
Question 48. In the figure, two equal circles, with centres 0 and O’, touch each other A at X. OO’ produced meets the circle with centre O’ at A. AC is tangent to the circle with centre O, at the point C. O’D is perpendicular to AC. Find the value of \(\frac{\mathrm{DO}^{\prime}}{\mathrm{CO}}\). (2016OD)

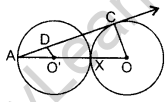
Solution:
Given: Two equal circles, with centres O and O’, touch each other at point X. OO’ is produced to meet the circle with centre (at A. AC is tangent to the circle with centre O, at the point C. OʻD is perpendicular to AC.
To find: = \(\frac{\mathrm{DO}^{\prime}}{\mathrm{CO}}\)
Proof: ∠ACO = 90° … [Tangent is ⊥ to the radius through the point of contact
In ∆AO’D and ∆AOC
∠O’AD = ∠OAC …(Common
∴ ∠ADO = ∠ACO …[Each 90°
∴ ∆AO’D ~ ∴AOC …(AA similarity
\(\frac{\mathrm{AO}^{\prime}}{\mathrm{AO}}=\frac{\mathrm{DO}^{\prime}}{\mathrm{CO}}\) … [In ~ As corresponding sides are proportional
\(\frac{r}{3 r}=\frac{\mathrm{DO}^{\prime}}{\mathrm{CO}}\) …[Let AO’ = O’X = OX = r ⇒ AO = r +r+ r = 3r
∴ \(\frac{\mathrm{DO}^{\prime}}{\mathrm{CO}}=\frac{1}{3}\)

Question 49. In the figure, l and m are two parallel tangents to a circle with centre O, touching the circle at A and B respectively. Another tangent at C intersects the line I at D and m at E. Prove that ∠DOE = 90°. (2013D)

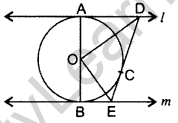
Solution:
Proof: Let I be XY and m be XY’
∠XDE + ∠X’ED = 180° … [Consecutive interior angles

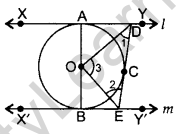
\(\frac{1}{2}\)XDE + \(\frac{1}{2}\)∠X’ED =
= \(\frac{1}{2}\) (180°)
= ∠1 + ∠2 = 90° …[OD is equally inclined to the tangents
In ∆DOE, ∠1 + ∠2 + 23 = 180° …[Angle-sum-property of a ∆
90° + 23 = 180°
⇒ ∠3 = 180° – 90o = 90°
∴ ∠DOE = 90° …(proved)

Question 50. In the figure, the sides AB, BC and CA of triangle ABC touch a circle with centre o and radius r at P, Q and R. respectively. (2013OD)
Prove that:
(i) AB + CQ = AC + BQ
(ii) Area (AABC) = \(\frac{1}{2}\) (Perimeter of ∆ABC ) × r

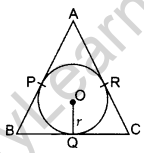
Solution:

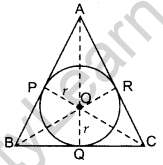
Part I:
Proof: AP = AR …(i)
BP = BQ … (ii)
CQ = CR … (iii)
Adding (i), (ii) & (iii)
AP + BP + CQ
= AR + BQ + CR
AB + CQ = AC + BQ
Part II: Join OP, OR, OQ, OA, OB and OC
Proof: OQ ⊥ BC; OR ⊥ AC; OP ⊥ AB
ar(∆ABC) = ar(∆AOB) + ar(∆BOC) + ar (∆AOC)
Area of (∆ABC)

Question 51. In the figure, a triangle ABC is drawn to circumscribe a circle of radius 4 cm, such that the segments BD and DC are of lengths 8 cm and 6 cm respectively. Find the sides AB and AC. (2014OD)

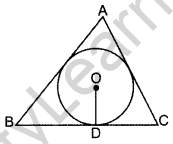
Solution:

Let AE = x ∴ AF = x
BC = 8 + 6 = 14 cm
AB = (x + 8) cm
AC = (x + 6) cm
∠1 = ∠2 = 23 = 90° …[ Tangent is ⊥ to the radius B [through the point of contact

\(4 \sqrt{3 x(x+14)}\) = 2(2x + 28)
\(4 \sqrt{3 x(x+14)}\) = 2.2(x + 14)
3x(x + 14) = (x + 14)² … [Squaring both sides
3x(x + 14) – (x + 14)² = 0
(x + 14) [3x – (x + 14)] = 0
(x + 14) (2x – 14) = 0
x = -14 or x = 7
∴ x = 7 … [As side of ∆ cannot be -ve
∴ AB = x + 8 = 15 cm
and AC = x + 6 = 13 cm

Question 52. rove that the line segment joining the points of contact of two parallel tangents of a circle, passes through its centre. (2014 D)
Solution:

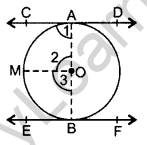
Given: CD and EF are two C parallel tangents at points A and B of a circle with centre O.
To prove: AB passes through centre O or AOB is diameter of the circle.
Const.: Join OA and OB. Draw OM || CD.
Proof: ∠1 = 90° … (i)
…[∵ Tangent is I to the radius through the point of contact
OM || CD
∴ ∠1 + ∠2 = 180° …(Co-interior angles
90° + ∠2 = 180° …[From (i)
∠2 = 180° – 90o = 90°
Similarly, ∠3 = 90°
∠2 + ∠3 = 90° + 90° = 180°
∴ AOB is a straight line.
Hence AOB is a diameter of the circle with centre O.
∴ AB passes through centre 0.