Surface Areas and Volumes Class 10 Extra Questions Maths Chapter 13

You can find important questions for Class 10 Maths Chapter 13, Surface Areas and Volumes, at IL. These questions are designed according to the updated syllabus and the latest exam pattern. If you’re getting ready for the CBSE exams in 2022-2023, practicing these questions can help you ace the Surface Areas and Volumes section and secure full marks. Additionally, checking out the Class 10 Notes on Surface Areas and Volumes can give you a quick summary of the key formulas. By solving these questions, you’ll build your confidence and be well-prepared for the Class 10 Maths exam.

Also Check: CBSE Class 10 Maths Important Question Chapter 8 Trig0nometry

Short Answer Type Questions

Q.1: A canal is 300 cm wide and 120 cm deep. The water in the canal is flowing at a speed of 20 km/h. How much area will it irrigate in 20 minutes if 8 cm of standing water is desired?

Solution:

The volume of water flows in the canal in one hour = width of the canal × depth

of the canal × speed of the canal water = 3 × 1.2 × 20 × 1000 m³

= 72000 m³

In 20 minutes the volume of water = (72000 × 20)/ 60 = 24000 m³

Area irrigated in 20 minutes, if 8 cm, i.e., 0.08 m standing water is required

=24000/0.08

= 300000 m²

= 30 hectares

Also Check: Important Questions for Class 10 Maths Chapter 14 Statistics

Q.2: Two cones have their heights in the ratio 1 : 3 and radii in the ratio 3 : 1. What is the ratio of their volumes?

Solution:

Given,

Ratio of heights of two cones = 1 : 3

Ratio of radii = 3 : 1

Let h and 3h be the height of two cones.

Also, 3r and r be the corresponding radii of cones.

So, r₁ = 3r, h₁ = h, r₂ = r, h₂ = 3h.

Ratio of volumes = [(1/3)πr₁²h₁]/ [(1/3)πr₂²h₂]

= [(3r)² h]/[r² (3h)]

= (9r²h)/(3r²h)

= 3/1

Hence, the ratio of volumes = 3 : 1

Q.3: A cubical ice-cream brick of edge 22 cm is to be distributed among some children by filling ice-cream cones of radius 2 cm and height 7 cm up to its brim. How many children will get the ice cream cones?

Solution:

Let n be the number of ice-cream cones.

Volume of cubical ice-cream brick = 22 cm × 22 cm × 22 cm

Radius of cone = r = 2 cm

Height of cone = h = 7 cm

Volume of cone = (1/3)πr²h = (1/3) × (22/7) × 2 × 2 × 7

So,

n × Volume of one cone = Volume of cubical ice-cream brick

n × (1/3) × (22/7) × 2 × 2 × 7 = 22 × 22 × 22

n × (1/3) × 4 = 22 × 22

n = (22 × 22 × 3)/4

n = 363

Therefore, 363 children will get the ice cream cones.

Also Check: Surface Areas and Volumes Class 10 Extra Questions Maths Chapter 13

Q.4: Three cubes of a metal whose edges are in the ratio 3:4:5 are melted and converted into a single cube whose diagonal is 12√3 cm. Find the edges of the three cubes.

Solution:

Let the edges of three cubes (in cm) be 3x, 4x and 5x, respectively.

Volume of the cubes after melting is = (3x)³ + (4x)³ + (5x)³ = 216x³ cm³

Let a be the side of a new cube so formed after melting.

Therefore, a³ = 216x³

So, a = 6x

Given that, diagonal of a single cube = 12√3 cm

i.e. √(a² + a² + a²) = 12√3

a√3 = 12√3

Therefore, a = 12

Thus, 12 = 6x

x = 2

Now, 3x = 3 × 2 = 6

4x = 4 × 2 = 8

5x = 5 × 2 = 10

Therefore, the edges of the three cubes are 6 cm, 8 cm and 10 cm, respectively.

Also Check: Polynomials Class 10 Extra Questions Maths Chapter 2

Q.5: Find the number of solid spheres each of diameter 6 cm that can be made by melting a solid metal cylinder of height 45 cm and diameter 4 cm.

Solution:

Given,

Diameter of solid sphere = 6 cm

Diameter of cylinder = 4 cm

Height of cylinder = h = 45 cm

Radius of sphere = r₁ = 6/2 = 3 cm

Radius of cylinder = r₂ = 4/2 = 2 cm

Let n be the number of spheres.

n × Volume of one sphere = Volume of cylinder

n × (4/3)πr₁³ = πr₂²h

n × (4/3) × (22/7) × 3 × 3 × 3 = (22/7) × 2 × 2 × 45

n × 9 = 45

n = 45/9

n = 5

Also Check: Some Applications of Trigonometry Class 10 Extra Questions Maths Chapter 9

Long Answer Type Questions

Q.1: Rasheed got a playing top (lattu) as his birthday present, which surprisingly had no colour on it. He wanted to colour it with his crayons. The top is shaped like a cone surmounted by a hemisphere. The entire top is 5 cm in height, and the diameter of the top is 3.5 cm. Find the area he has to colour. (Take π = 22/7)

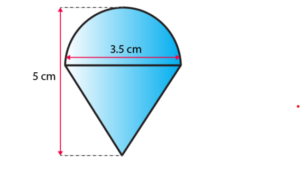
Solution:

TSA of the toy = CSA of hemisphere + CSA of cone

Curved surface area of the hemisphere = 1/ 2 (4πr²) = 2π r² = 2(22/7)× (3.5/2) × (3.5/2) = 19.25 cm²

Height of the cone = Height of the top – Radius of the hemispherical part

= (5 – 3.5/2) cm = 3.25 cm

Therefore, CSA of cone = πrl = (22/7) × (3.5/2) × 3.7 = 20.35 cm²

Hence, the surface area of the top = [2(22/7)× (3.5/2) × (3.5/2) + (22/7) × (3.5/2) × 3.7] cm²

= (22/7) × (3.5/2) (3.5+3.7) cm²

= (11/2) × (3.5 + 3.7) cm²

= 39.6 cm² (approx.)

Q. 2: Mayank made a bird-bath for his garden in the shape of a cylinder with a hemispherical depression at one end, as shown in the figure. The height of the cylinder is 1.45 m, and its radius is 30 cm. Find the total surface area of the bird-bath. (Take π = 22/7)

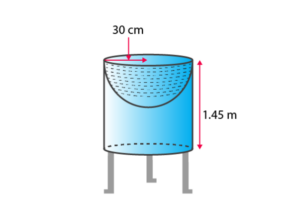
Solution:

Let h be the height of the cylinder and r be the common radius of the cylinder and hemisphere. Then, the total surface area of the bird-bath = CSA of cylinder + CSA of the hemisphere

= 2πrh + 2πr²

= 2π r(h + r)

= 2 (22/7) × 30 × (145 + 30) cm²

= 33000 cm² = 3.3 m²

Q.3: 2 cubes each of volume 64 cm³ are joined end to end. Find the surface area of the resulting cuboid.

Solution:

The diagram will obtain as below:

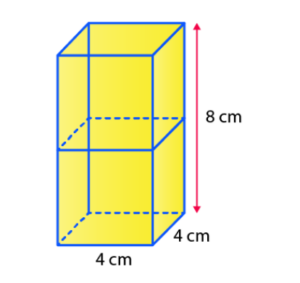
Given,

The Volume (V) of each cube is = 64 cm³

This implies that a³ = 64 cm³

∴ The side of the cube, i.e. a = 4 cm

Also, the breadth and length of the resulting cuboid will be 4 cm each while its height will be 8 cm.

So, the surface area of the cuboid (TSA) = 2(lb + bh + lh)

Now, by putting the values, we get,

= 2(8×4 + 4×4 + 4×8) cm²

= (2 × 80) cm²

Hence, TSA of the cuboid = 160 cm²

Q. 4: A tent is in the shape of a cylinder surmounted by a conical top. If the height and diameter of the cylindrical part are 2.1 m and 4 m respectively, and the slant height of the top is 2.8 m, find the area of the canvas used for making the tent. Also, find the cost of the canvas of the tent at the rate of Rs. 500 per m². (Note that the base of the tent will not be covered with canvas.)

Solution:

It is known that a tent is a combination of a cone and a cylinder, as shown below.

From the question, we know that

The diameter = D = 4 m

l = 2.8 m (slant height)

The radius of the cylinder is equal to the radius of the cylinder

So, r = 4/2 = 2 m

Also, we know the height of the cylinder (h) is 2.1 m

So, the required surface area of the given tent = surface area of the cone (the top) + surface area of the cylinder(the base)

= πrl + 2πrh

= πr (l+2h)

Now, substituting the values and solving it we get the value as 44 m²

∴ The cost of the canvas at the rate of Rs. 500 per m² for the tent will be

= Surface area × cost/ m²

= 44 × 500

So, Rs. 22000 will be the total cost of the canvas.

Q. 5: A solid toy is in the form of a hemisphere surmounted by a right circular cone. The height of the cone is 2 cm, and the diameter of the base is 4 cm. Determine the volume of the toy. If a right circular cylinder circumscribes the toy, find the difference between the volumes of the cylinder and the toy. (Take π = 3.14)

Solution:

Let BPC be the hemisphere and ABC be the cone standing on the base of the hemisphere as shown in the above figure.

The radius BO of the hemisphere (as well as of the cone) =( ½) × 4 cm = 2 cm.

So, volume of the toy = (⅔) πr³ + (⅓) πr²h

= (⅔) × 3.14 × 2³ + (⅓)× 3.14 × 2² × 2

= 25.12 cm³

Now, let the right circular cylinder EFGH circumscribe the given solid.

The radius of the base of the right circular cylinder = HP = BO = 2 cm, and its height is

EH = AO + OP = (2 + 2) cm = 4 cm

So, the volume required = volume of the right circular cylinder – the volume of the toy

= (3.14 × 2² × 4 – 25.12) cm³

= 25.12 cm³

Hence, the required difference between the two volumes = 25.12 cm³

Q. 6: A spherical glass vessel has a cylindrical neck 8 cm long, 2 cm in diameter; the diameter of the spherical part is 8.5 cm. By measuring the amount of water it holds, a child finds its volume to be 345 cm³. Check whether she is correct, taking the above as the inside measurements, and π = 3.14.

Solution:

Given,

For the cylinder part, Height (h) = 8 cm and Radius (R) = (2/2) cm = 1 cm

For the spherical part, Radius (r) = (8.5/2) = 4.25 cm

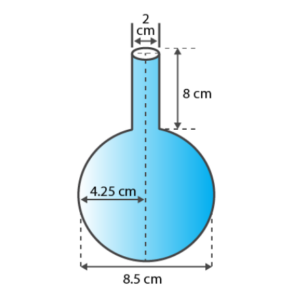
Now, the volume of this vessel = Volume of cylinder + Volume of a sphere

= π × (1)² × 8 + (4/3) π (4.25)³
= 25.12 + 321.6
= 346.67 cm³

Q. 7: A cone of height 24 cm and radius of base 6 cm is made up of modelling clay. A child reshapes it in the form of a sphere. Find the radius of the sphere.

Solution:

The volume of cone = (⅓) × π × 6 × 6 × 24 cm³

If r is the radius of the sphere, then its volume is (4/3) πr³.

Since the volume of clay in the form of the cone and the sphere remains the same, we

Have (4/3) πr³ = (⅓) × π × 6 × 6 × 24 cm³

r³ = 3 × 3 × 24 = 3³ × 2³

So, r = 3 × 2 = 6

Therefore, the radius of the sphere is 6 cm.

Q. 8: Selvi’s house has an overhead tank in the shape of a cylinder. This is filled by pumping water from a sump (an underground tank) which is in the shape of a cuboid. The sump has dimensions 1.57 m × 1.44 m × 95cm. The overhead tank has a radius of 60 cm and a height of 95 cm. Find the height of the water left in the sump after the overhead tank has been completely filled with water from the sump which had been full. Compare the capacity of the tank with that of the sump. (Use π = 3.14)

Solution:

The volume of water in the overhead tank equals the volume of the water removed from the sump.

Now, the volume of water in the overhead tank (cylinder) = πr²h

= 3.14 × 0.6 × 0.6 × 0.95 m³

The volume of water in the sump when full = l × b × h = 1.57 × 1.44 × 0.95 m³

The volume of water left in the sump after filling the tank

= [(1.57 × 1.44 × 0.95) – (3.14 × 0.6 × 0.6 × 0.95)] m³ = (1.57 × 0.6 × 0.6 × 0.95 × 2) m³

Height of the water left in the sump = (volume of water left in the sump)/ (l × b)

= (1.57× 0.6× 0.6× 0.95 ×2)/ (1.57 ×1.44)

= 0.475 m

= 47.5 cm

Capacity of tank / Capacity of sump = (3.14 × 0.6 × 0.6 × 0.95)/ (1.57 × 1.44 × 0.95)

= 1/ 2

Therefore, the capacity of the tank is half the capacity of the sump.

Q. 9: Metallic spheres of radii 6 cm, 8 cm and 10 cm, respectively, are melted to form a single solid sphere. Find the radius of the resulting sphere.

Solution:

For Sphere 1:

Radius (r₁) = 6 cm

∴ Volume (V₁) = (4/3) × π× r₁³

For Sphere 2:

Radius (r₂) = 8 cm

∴ Volume (V₂) = (4/3) × π × r₂³

For Sphere 3:

Radius (r₃) = 10 cm

∴ Volume (V₃) = (4/3) × π× r₃³

Also, let the radius of the resulting sphere be “r”

Now, Volume of resulting sphere = V₁ + V₂ + V₃

(4/3)× π× r³ = (4/3)× π× r₁³ + (4/3)× π× r₂³ + (4/3) × π× r₃³

r³ = 6³ + 8³ + 10³

r³ = 1728

r = 12 cm

Q. 10: An open metal bucket is in the shape of a frustum of a cone, mounted on a hollow cylindrical base made of the same metallic sheet as shown in the figure. The diameters of the two circular ends of the bucket are 45 cm and 25 cm, the total vertical height of the bucket is 40 cm and that of the cylindrical base is 6 cm. Find the area of the metallic sheet used to make the bucket, where we do not take into account the handle of the bucket. Also, find the volume of water the bucket can hold. (Take π = 22/7)

Solution:

The total height of the bucket = 40 cm, which includes the height of the base.

So, the height of the frustum of the cone = (40 – 6) cm = 34 cm.

where r₁ = 22.5 cm, r₂ = 12.5 cm and h = 34 cm.

=35.44 cm

The area of metallic sheet used = curved surface area of frustum of cone + area of circular base + curved surface area of cylinder

= [π × 35.44 (22.5 + 12.5) + π × (12.5)² + 2π × 12.5 × 6] cm²

= 22/7 (1240.4 + 156.25 + 150) cm²

= 4860.9 cm²

Now, the volume of water that the bucket can hold (also, known as the capacity

of the bucket)

= (πh)/3 × (r₁² + r₂² + r₁r₂)

=(22/7) × (34/3) × [(22.5)² + (12.5)² + (22.5)(12.5)]

=(22/7) × (34/3) × 943.75

= 33615.48 cm³

= 33.62 litres (approx.)