Important Questions for Class 10 Maths Chapter 1 – Real Numbers

Chapter 1 of Class 10 Maths, Real Numbers, lays the foundation for higher-level mathematics by exploring concepts like Euclid’s Division Lemma, Fundamental Theorem of Arithmetic, decimal expansions, HCF and LCM, and irrational numbers. Mastering this chapter is essential for scoring well in exams, as it forms the basis for more advanced concepts.

What is Real Number?

Real numbers is a combination of rational and irrational numbers. They are the numbers upon which we easily perform mathematical operations. All the numbers are not imaginary are real numbers. For example, 33, -11, 7.99, 3/2, π(3.14), √2, etc.

Also Check:

• NCERT Solutions for Class 10
• NCERT Solutions for Class 10 Science
• NCERT Solutions for Class 10 English
• NCERT Solutions for Class 10 Social Science

Class 10 Real Numbers Important Questions and Answers

Question 1. The decimal expansion of the rational number \(\frac { 43 }{ { 2 }^{ 4 }{ 5 }^{ 3 } }\) will terminate after how many places of decimals? (2013)

Solution:

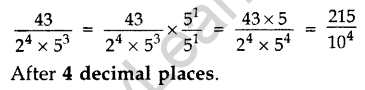
Question 2. Write the decimal form of \(\frac { 129 }{ { 2 }^{ 7 }{ 5 }^{ 7 }{ 7 }^{ 5 } }\)

Solution: Non-terminating non-repeating.

Also Check: Important Questions for Class 10 Maths Chapter 14 Statistics

Question 3. Find the largest number that will divide 398, 436 and 542 leaving remainders 7, 11, and 15 respectively.

Solution: Algorithm

398 – 7 = 391, 436 – 11 = 425, 542 – 15 = 527

HCF of 391, 425, 527 = 17

Question 4. Express 98 as a product of its primes.

Solution: 2 × 7²

Question 5. If the HCF of 408 and 1032 is expressible in the form 1032 × 2 + 408 × p, then find the value of p.

Solution:

HCF of 408 and 1032 is 24.

1032 × 2 + 408 × (p) = 24

408p = 24 – 2064

p = -5

Key Topics Covered in Real Numbers

Euclid’s Division Lemma

Euclid’s Division Lemma states that for any two positive integers, ‘a’ and ‘b,’ there exist unique integers ‘q’ (quotient) and ‘r’ (remainder) such that a=bq+ra = bq + ra=bq+r, where 0≤r<b0 \leq r < b0≤r<b.

Fundamental Theorem of Arithmetic

The Fundamental Theorem of Arithmetic states that every composite number can be expressed as a product of prime numbers in a unique way.

Decimal Expansions of Real Numbers

Decimal expansion defines whether a number’s decimal representation is terminating or non-terminating recurring. For instance, fractions like 1/2 and 1/5 have terminating decimals, while numbers like 1/3 have non-terminating recurring decimals.

HCF and LCM Using Prime Factorization and Euclid’s Algorithm

The HCF (Highest Common Factor) and LCM (Least Common Multiple) of two numbers can be calculated using prime factorization or Euclid’s algorithm.

Irrational Numbers

Irrational numbers are numbers that cannot be expressed as a fraction of two integers. They have non-terminating and non-repeating decimal expansions. Common examples include √2, √3, and π.

 

Also Check: Surface Areas and Volumes Class 10 Extra Questions Maths Chapter 13

Real Numbers Class 10 Important Questions Short Answer-I (2 Marks)

Question 6. HCF and LCM of two numbers is 9 and 459 respectively. If one of the numbers is 27, find the other number. (2012)
Solution:
We know,
1st number × 2nd number = HCF × LCM
⇒ 27 × 2nd number = 9 × 459
⇒ 2nd number = \(\frac { 9\times 459 }{ 27 }\) = 153

Question 7. Find HCF and LCM of 13 and 17 by prime factorisation method. (2013)

Solution:

13 = 1 × 13; 17 = 1 × 17

HCF = 1 and LCM = 13 × 17 = 221

Question 8. Find LCM of numbers whose prime factorisation are expressible as 3 × 5² and 3² × 7². (2014)

Solution:

LCM (3 × 5², 3² × 7²) = 3² × 5² × 7² = 9 × 25 × 49 = 11025

Also Check: Polynomials Class 10 Extra Questions Maths Chapter 2

Question 9. Find the LCM of 96 and 360 by using fundamental theorem of arithmetic. (2012)

Solution:

96 = 2⁵ × 3

360 = 2³ × 3² × 5

LCM = 2⁵ × 3² × 5 = 32 × 9 × 5 = 1440

Question 10. Find the HCF (865, 255) using Euclid’s division lemma. (2013)

Solution:

865 > 255

865 = 255 × 3 + 100

255 = 100 × 2 + 55

100 = 55 × 1 + 45

55 = 45 × 1 + 10

45 = 10 × 4 + 5

10 = 5 × 2 + 0

The remainder is 0.

HCF = 5

Question 11. Find the largest number which divides 70 and 125 leaving remainder 5 and 8 respectively. (2015)

Solution:

It is given that on dividing 70 by the required number, there is a remainder 5.

This means that 70 – 5 = 65 is exactly divisible by the required number.

Similarly, 125 – 8 = 117 is also exactly divisible by the required number.

65 = 5 × 13

117 = 3² × 13

HCF = 13

Required number = 13

Question 12. Find the prime factorisation of the denominator of rational number expressed as \(6.\bar { 12 }\) in simplest form. (2014)

Solution:

Let x = \(6.\bar { 12 }\) …(i)

100x = 612.\(\bar { 12 }\) …(ii)…[Multiplying both sides by 100]

Subtracting (i) from (ii),

99x = 606

x = \(\frac { 606 }{ 99 }\) = \(\frac { 202 }{ 33 }\)

Denominator = 33

Prime factorisation = 3 × 11

Also Check: Some Applications of Trigonometry Class 10 Extra Questions Maths Chapter 9

Question 13. Complete the following factor tree and find the composite number x. (2014)

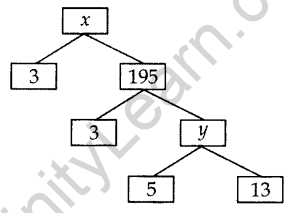
Solution:
y = 5 × 13 = 65
x = 3 × 195 = 585

Question 14. Prove that 2 + 3√5 is an irrational number. (2014)

Solution:

Let us assume, to the contrary, that 2 + 3√5 is rational.

So that we can find integers a and b (b ≠ 0).

Such that 2 + 3√5 = \(\frac { a }{ b }\), where a and b are coprime.

Rearranging the above equation, we get

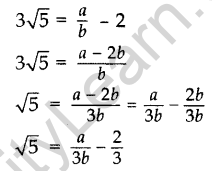
Since a and b are integers, we get \(\frac { a }{ 3b } -\frac { 2 }{ 3 }\) is rational and so √5 is rational. But this contradicts the fact that √5 is irrational. So, we conclude that 2 + 3√5 is irrational.

Question 15. Show that 3√7 is an irrational number. (2016)

Solution: Let us assume, to the contrary, that 3√7 is rational.

That is, we can find coprime a and b (b ≠ 0) such that 3√7 = \(\frac { a }{ b }\)

Rearranging, we get √7 = \(\frac { a }{ 3b }\)

Since 3, a and b are integers, \(\frac { a }{ 3b }\) is rational, and so √7 is rational.

But this contradicts the fact that √7 is irrational.

So, we conclude that 3√7 is irrational.

Enroll Now to Online Course for JEE Class 10 Preparation

Question 16. Explain why (17 × 5 × 11 × 3 × 2 + 2 × 11) is a composite number? (2015)

Solution:

17 × 5 × 11 × 3 × 2 + 2 × 11 …(i)

= 2 × 11 × (17 × 5 × 3 + 1)

= 2 × 11 × (255 + 1)

= 2 × 11 × 256

Number (i) is divisible by 2, 11 and 256, it has more than 2 prime factors. Therefore (17 × 5 × 11 × 3 × 2 + 2 × 11) is a composite number.

Also Check: Important Questions Class 10 Maths Chapter 4 Quadratic Equations

Question 17. Check whether 4n can end with the digit 0 for any natural number n. (2015)

Solution:

4ⁿ = (2²)ⁿ = 2²ⁿ

The only prime in the factorization of 4ⁿ is 2.

There is no other prime in the factorization of 4ⁿ = 2²ⁿ

(By uniqueness of the Fundamental Theorem of Arithmetic).

5 does not occur in the prime factorization of 4ⁿ for any n.

Therefore, 4ⁿ does not end with the digit zero for any natural number n.

Question 18. Can two numbers have 15 as their HCF and 175 as their LCM? Give reasons. (2017 OD)

Solution:

No, LCM = Product of the highest power of each factor involved in the numbers.

HCF = Product of the smallest power of each common factor.

We can conclude that LCM is always a multiple of HCF, i.e., LCM = k × HCF

We are given that,

LCM = 175 and HCF = 15

175 = k × 15

⇒ 11.67 = k

But in this case, LCM ≠ k × HCF

Therefore, two numbers cannot have LCM as 175 and HCF as 15.

Real Numbers Class 10 Important Questions Short Answer-II (3 Marks)

Question 19. Prove that √5 is irrational and hence show that 3 + √5 is also irrational. (2012)

Solution: Let us assume, to the contrary, that √5 is rational.

So, we can find integers p and q (q ≠ 0), such that

√5 = \(\frac { p }{ q }\), where p and q are coprime.

Squaring both sides, we get

5 = \(\frac { { p }^{ 2 } }{ { q }^{ 2 } }\)

⇒ 5q² = p² …(i)

⇒ 5 divides p²

5 divides p

So, let p = 5r

Putting the value of p in (i), we get

5q² = (5r)²

⇒ 5q² = 25r²

⇒ q² = 5r²

⇒ 5 divides q²

5 divides q

So, p and q have atleast 5 as a common factor.

But this contradicts the fact that p and q have no common factor.

So, our assumption is wrong, is irrational.

√5 is irrational, 3 is a rational number.

So, we conclude that 3 + √5 is irrational.

Question 20. Prove that 3 + 2√3 is an irrational number. (2014)

Solution:

Let us assume to the contrary, that 3 + 2√3 is rational.

So that we can find integers a and b (b ≠ 0).

Such that 3 + 2√3 = \(\frac { a }{ b }\), where a and b are coprime.

Rearranging the equations, we get

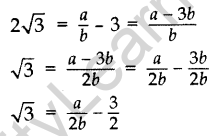
Since a and b are integers, we get \(\frac { a }{ 2b } -\frac { 3 }{ 2 }\) is rational and so √3 is rational. But this contradicts the fact that √3 is irrational. So we conclude that 3 + 2√3 is irrational.

Question 21. Three bells toll at intervals of 9, 12, 15 minutes respectively. If they start tolling together, after what time will they next toll together? (2013)

Solution:

9 = 3², 12 = 2² × 3, 15 = 3 × 5

LCM = 2² × 3² × 5 = 4 × 9 × 5 = 180 minutes or 3 hours

They will next toll together after 3 hours.

Enroll Now to Online Course for NEET Class 10 Preparation

Question 22. Two tankers contain 850 liters and 680 liters of petrol. Find the maximum capacity of a container which can measure the petrol of each tanker in the exact number of times. (2012)

Solution: To find the maximum capacity of a container which can measure the petrol of each tanker in the exact number of times, we find the HCF of 850 and 680.

850 = 2 × 5² × 17

680 = 2³ × 5 × 17

HCF = 2 × 5 × 17 = 170

Maximum capacity of the container = 170 liters.

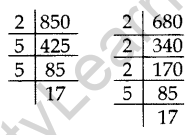
Question 23. The length, breadth, and height of a room are 8 m 50 cm, 6 m 25 cm and 4 m 75 cm respectively. Find the length of the longest rod that can measure the dimensions of the room exactly. (2015)

Solution: To find the length of the longest rod that can measure the dimensions of the room exactly, we have to find HCF.

L, Length = 8 m 50 cm = 850 cm = 2¹ × 5² × 17

B, Breadth = 6 m 25 cm = 625 cm = 5⁴

H, Height = 4 m 75 cm = 475 cm = 5² × 19

HCF of L, B and H is 5² = 25 cm

Length of the longest rod = 25 cm

Question 24. Three alarm clocks ring at intervals of 4, 12 and 20 minutes respectively. If they start ringing together, after how much time will they next ring together? (2015)

Solution: To find the time when the clocks will next ring together,

we have to find LCM of 4, 12 and 20 minutes.

4 = 2²
12 = 2² × 3
20 = 2² × 5

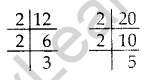
LCM of 4, 12 and 20 = 2² × 3 × 5 = 60 minutes. So, the clocks will ring together again after 60 minutes or one hour.

Question 25. In a school, there are two Sections A and B of class X. There are 48 students in Section A and 60 students in Section B. Determine the least number of books required for the library of the school so that the books can be distributed equally among all students of each Section. (2017 OD)

Solution: Since the books are to be distributed equally among the students of Section A and Section B. therefore, the number of books must be a multiple of 48 as well as 60.

Hence, required number of books is the LCM of 48 and 60.

48 = 2⁴ × 3

60 = 2² × 3 × 5

LCM = 2⁴ × 3 × 5 = 16 × 15 = 240

Hence, required number of books is 240.

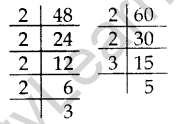
Question 26. By using Euclid’s algorithm, find the largest number which divides 650 and 1170. (2017 OD)

Solution:

Given numbers are 650 and 1170.

1170 > 650

1170 = 650 × 1 + 520

650 = 520 × 1 + 130

520 = 130 × 4 + 0

HCF = 130

The required largest number is 130.

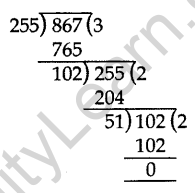
Question 27. Find the HCF of 255 and 867 by Euclid’s division algorithm. (2014)

Solution:

867 is greater than 255. We apply the division lemma to 867 and 255, to get

867 = 255 × 3 + 102

We continue the process till the remainder is zero

255 = 102 × 2 + 51

102 = 51 × 2 + 0, the remainder is zero.

HCF = 51

Question 28.Using Euclid’s division algorithm, find whether the pair of numbers 847, 2160 are coprime or not. To find out the minimum (least) time when the bells toll together next, we find the LCM of 9, 12, 15.

Solution:

Real Numbers Class 10 Important Questions Long Answer (4 Marks)

Question 29. Prove that 3 + 2√5 is irrational. (2012, 2017 D)

Solution:

Let us assume, to the contrary, that 3 + 2√5 is rational

So that we can find integers a and b (b ≠ 0), such that

3 + 2 √5 = \(\frac { a }{ b }\), where a and b are coprime.

Rearranging this equation, we get

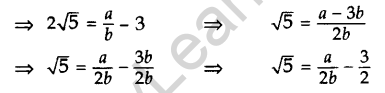
Since a and b are integers, we get that \(\frac { a }{ 2b }\) – \(\frac { 3 }{ 2 }\) is rational and so √5 is rational. But this contradicts the fact that √5 is irrational.
So we conclude that 3 + 2√5 is irrational.

Question 30. There are 104 students in class X and 96 students in class IX in a school. In a house examination, the students are to be evenly seated in parallel rows such that no two adjacent rows are of the same class. (2013)

(a) Find the maximum number of parallel rows of each class for the seating arrange¬ment.

(b) Also, find the number of students of class IX and also of class X in a row.

(c) What is the objective of the school administration behind such an arrangement?

Solution:

104 = 2³ × 13

96 = 2⁵ × 3

HCF = 2³ = 8

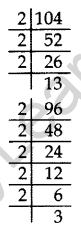
(a) Number of rows of students of class X = \(\frac { 104 }{ 8 }\) = 13

Number maximum of rows class IX = \(\frac { 96 }{ 8 }\) = 12

Total number of rows = 13 + 12 = 25

(b) No. of students of class IX in a row = 8

No. of students of class X in a row = 8

(c) The objective of school administration behind such an arrangement is fair and clean examination, so that no student can take help from any other student of his/her class.

Question 31. Dudhnath has two vessels containing 720 ml and 405 ml of milk respectively. Milk from these containers is poured into glasses of equal capacity to their brim. Find the minimum number of glasses that can be filled. (2014)
Solution:

1st vessel = 720 ml; 2nd vessel = 405 ml

We find the HCF of 720 and 405 to find the maximum quantity of milk to be filled in one glass.

405 = 3⁴ × 5

720 = 2⁴ × 3² × 5

HCF = 3² × 5 = 45 ml = Capacity of glass

No. of glasses filled from 1st vessel = \(\frac { 720 }{ 45 }\) = 16

No. of glasses filled from 2nd vessel = \(\frac { 405 }{ 45 }\) = 9

Total number of glasses = 25

Question 32. Amita, Sneha, and Raghav start preparing cards for all persons of an old age home. In order to complete one card, they take 10, 16 and 20 minutes respectively. If all of them started together, after what time will they start preparing a new card together? (2013)

Solution:

To find the earliest (least) time, they will start preparing a new card together, we find the LCM of 10, 16 and 20.

10 = 2 × 5

16 = 2⁴

20 = 2² × 5

LCM = 2⁴ × 5 = 16 × 5 = 80 minutes

They will start preparing a new card together after 80 minutes.

Question 33. Find HCF of numbers 134791, 6341 and 6339 by Euclid’s division algorithm. (2015)

Solution:

First, we find HCF of 6339 and 6341 by Euclid’s division method.

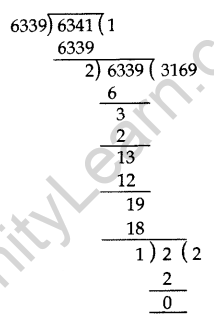
6341 > 6339

6341 = 6339 × 1 + 2

6339 = 2 × 3169 + 1

2 = 1 × 2 + 0

HCF of 6341 and 6339 is 1.

Now, we find the HCF of 134791 and 1

134791 = 1 × 134791 + 0

HCF of 134791 and 1 is 1.

Hence, the HCF of the given three numbers is 1.

Question 34. If two positive integers x and y are expressible in terms of primes as x = p²q³ and y = p³q, what can you say about their LCM and HCF. Is LCM a multiple of HCF? Explain. (2014)

Solution:

x = p²q³ and y = p³q

LCM = p³q³

HCF = p²q …..(i)

Now, LCM = p³q³

⇒ LCM = pq² (p²q)

⇒ LCM = pq² (HCF)

Yes, LCM is a multiple of HCF.

Explanation:

Let a = 12 = 2² × 3

b = 18 = 2 × 3²

HCF = 2 × 3 = 6 …(ii)

LCM = 2² × 3² = 36

LCM = 6 × 6

LCM = 6 (HCF) …[From (ii)]

Here LCM is 6 times HCF.

Question 35. Show that one and only one out of n, (n + 1) and (n + 2) is divisible by 3, where n is any positive integer. (2015)

Solution:

Let n, n + 1, n + 2 be three consecutive positive integers.

We know that n is of the form 3q, 3q + 1, or 3q + 2.

Case I. When n = 3q,

In this case, n is divisible by 3,

but n + 1 and n + 2 are not divisible by 3.

Case II. When n = 3q + 1,

In this case n + 2 = (3q + 1) + 2

= 3q + 3

= 3(q + 1 ), (n + 2) is divisible by 3,

but n and n + 1 are not divisible by 3.

Case III.

When n = 3q + 2, in this case,

n + 1 = (3q + 2) + 1

 

= 3q + 3 = 3 (q + 1 ), (n + 1) is divisible by 3,

but n and n + 2 are not divisible by 3.

Hence, one and only one out of n, n + 1 and n + 2 is divisible by 3.

Question 36. Find the HCF and LCM of 306 and 657 and verify that LCM × HCF = Product of the two numbers. (2016 D)

Solution:

306 = 2 × 3² × 17

657 = 32 × 73

HCF = 3² = 9

LCM = 2 × 3² × 17 × 73 = 22338

L.H.S. = LCM × HCF = 22338 × 9 = 201042

R.H.S. = Product of two numbers = 306 × 657 = 201042

L.H.S. = R.H.S.

Question 37. Show that any positive odd integer is of the form 41 + 1 or 4q + 3 where q is a positive integer. (2016 OD)

Solution: Let a be a positive odd integer

By Euclid’s Division algorithm:

a = 4q + r …[where q, r are positive integers and 0 ≤ r < 4]

a = 4q

or 4q + 1

or 4q + 2

or 4q + 3

But 4q and 4q + 2 are both even

a is of the form 4q + 1 or 4q + 3.

Additional Tips for Exam Preparation

1. Practice with Previous Year’s Papers: Solving past questions helps identify important question patterns and familiarizes you with the exam format.
2. Revise Key Formulas: Focus on formulas related to HCF, LCM, and proofs of irrationality.
3. Make Use of NCERT Solutions: Refer to NCERT Solutions for Class 10 Maths to solidify your understanding of key concepts. Detailed solutions in these resources provide clarity on how to approach different types of problems.
4. Focus on Neat and Organized Answers: Write your answers in a clear and organized manner. For questions involving proofs or lengthy calculations, structure your work to make it easy for the examiner to follow.
5. Time Management: Use a timer when solving sample papers to enhance your speed and accuracy. This will prepare you to complete the actual exam on time without feeling rushed.

Frequently Asked Questions (FAQs)

[sc_fs_multi_faq headline-0=”h3″ question-0=”What is Euclid’s Division Lemma in Class 10 Maths?” answer-0=”Euclid’s Division Lemma states that for any two positive integers a and b, there exist unique integers q and r such that a=bq+r, where 0≤r​