CBSE Previous Year Question Papers Class 10 Maths SA2 Delhi – 2012

Time allowed: 3 hours Maximum marks: 90

GENERAL INSTRUCTIONS:

1. All questions are compulsory.
2. The Question Taper consists of 31 questions divided into four Sections A, B. C. and D.
3. Section A contains 4 questions of 1 mark each. Section B contains 6 questions of 2 marks each, Section C contains 10 questions of 3 marks each and Section D contains 11 questions of 4 marks each.
4. Use of calculators is not permitted.

SET I

SECTION A
Questions number 1 to 4 carry 1 mark each.
Question.1 If 1 is a root of the equations ay² + ay + 3 = 0 and y² + y + b = 0, then find the value of ab.
Solution.

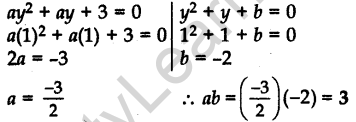
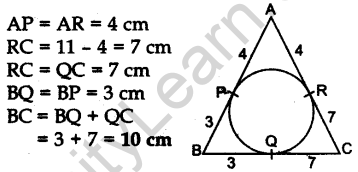
Question.2 In Fig. 1, the sides AB, BC and CA of a triangle ABC touch a circle at P, Q and R respectively. If PA = 4 cm, BP = 3 cm and AC = 11 cm, find the length of BC (in cm).

Solution.

Question.3 In Fig. 2, a circle touches the side DF of ΔEDF at H and touches ED and EF produced at K and M respectively. If EK = 9 cm, calculate the perimeter of ΔEDF (in cm).

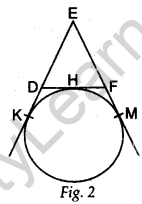
Solution.

Question.4 If the area of a circle is equal to sum of the areas of two circles of diameters 10 cm and 24 cm, calculate the diameter of the larger circle (in cm).
Solution.

SECTION B
Questions number 5 to 10 carry 2 marks each.
Question.5 Find the sum of the first 25 terms of an A.P. whose n^th term is given by t_n= 2 – 3n.
Solution.

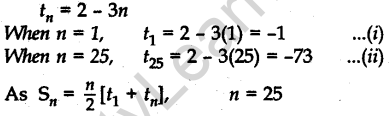
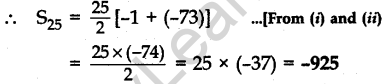
Question.6 In a simultaneous toss of two coins, find the probability of getting:
(i) exactly one head, (ii) atmost one head.
Solution.

Question.7 Find the value(s) of k so that the quadratic equation x² – 4kx + k = 0 has equal roots.
Solution.

Question.8 Find the sum of all three digit natural numbers, which are multiples of 11.
Solution.

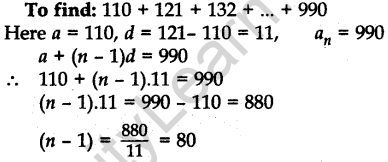
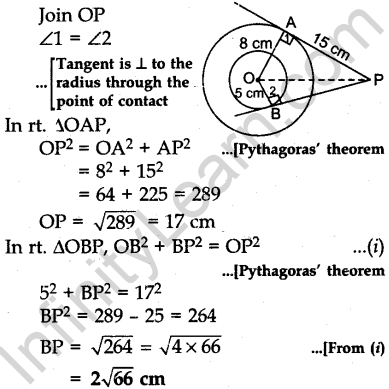
Question.9 Tangents PA and PB are drawn from an external point P to two concentric circles with centre O and radii 8 cm and 5 cm respectively, as shown in Fig. 3. If AP = 15 cm, then find the length of BP.

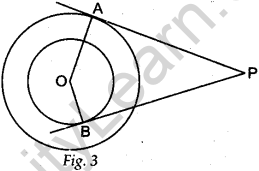
Solution.

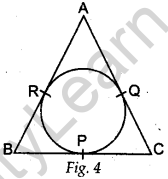
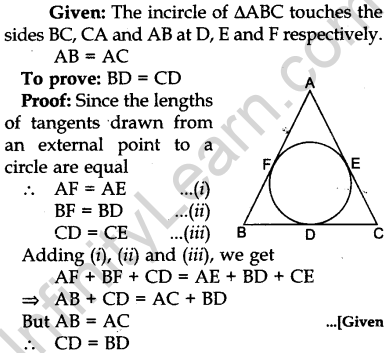
Question.10 In Fig. 4, an isosceles triangle ABC, with AB = AC, circumscribes a circle. Prove that the point of contact P bisects the base BC.

Or
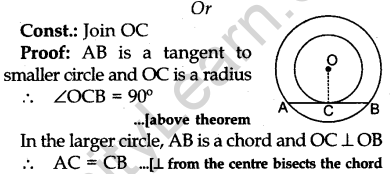
In Fig. 5, the chord AB of the larger of the two concentric circles, with centre O, touches the smaller circle at C. Prove that AC = CB.

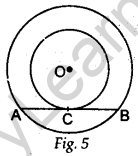
Solution.

SECTION C
Questions number 11 to 20 carry 3 marks each.
Question.11 A milkman was serving his customers using two types of mugs A and B of inner diameter 5 cm to serve the customers. The height of the mugs is 10 cm.
He decided to serve the customers in ‘B’ type of mug.
(a) Find the volume of the mugs of both types.
(b) Which mathematical concept is used in the above problem?
(c) By chasing the mug of type ‘B’, which value is being depicted MUg ‘A’ bv the milkman?

Solution.

Question.12 In Fig. 6, OABC is a square of side 7 cm. If OAPC is a quadrant of a circle with centre O, then find the area of the shaded region.
[Use π = 22/7 ]

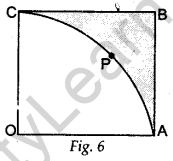
Solution.

Question.13 If a point A(0, 2) is equidistant from the points B(3, p) and C(p, 5), then find the value of p,
Solution.

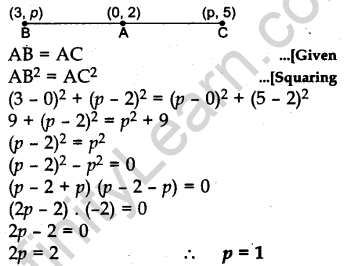
Question.14 A number is selected at random from first 50 natural numbers. Find the probability that it is a multiple of 3 and 4.
Solution.

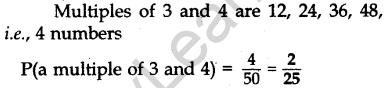
Question.15 Solve for x: 4×2 – 4ax + (a² – b²) = 0
Or
Solve for x: 3x² – 2√6x + 2 = 0
Solution.

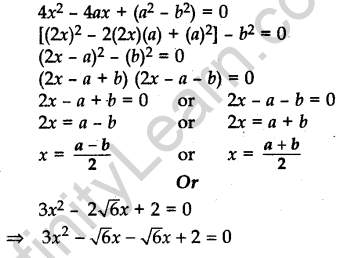
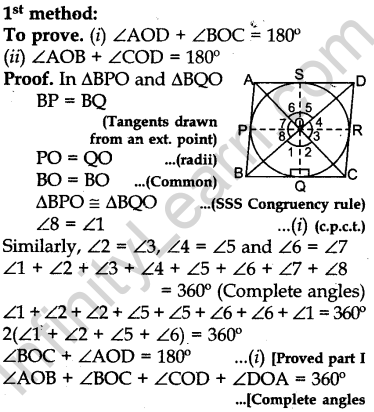
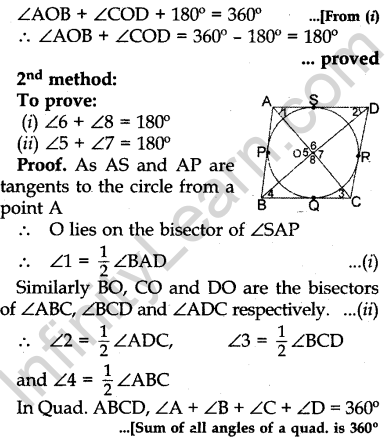
Question.16 Prove that the parallelogram circumscribing a circle is a rhombus.
Or
Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
Solution.

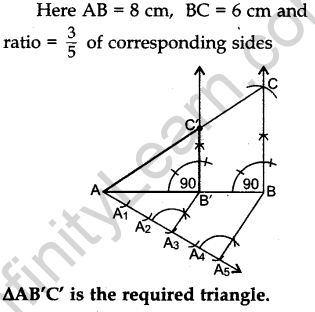
Question.17 Construct a right triangle in which the sides, (other than the hypotenuse) are of length 6 cm
and 8 cm. Then construct another triangle, whose sides are 3/5 times the corresponding sides of the given triangle.
Solution.

Question.18 In Fig. 7, PQ and AB are respectively the arcs of two concentric circles of radii 7 cm and 3.5 cm and centre O. If ∠POQ = 30°
then find the area of the shaded region. [Use π= 22/7 ]

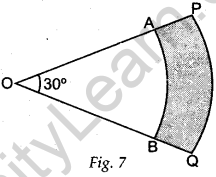
Solution.

Question.19 From a solid cylinder of height 7 cm and base diameter 12 cm, a conical cavity of same height and same base diameter is hollowed out. Find the total surface area of the remaining
solid. [Use π = 22/7 ]
Or
A cylindrical bucket, 32 cm high and with radius of base 18 cm, is filled with sand. This bucket is emptied on the ground and a conical heap of sand is formed. If the height of the conical heap is 24 cm, then find the radius and slant height of the heap.
Solution.

Question.20 The angles of depression* of two ships from the top of a light house and on the same side of it are found to be 45° and 30°. If the ships are 200 m apart, find the height of the light house.
Solution.

SECTION D
Questions number 21 to 31 carry 4 marks each.
Question.21 A point P divides the line segment joining the points A(3, -5) and B(-4, 8) such that AP K
pg = Y . If P lies on the line x + y = 0, then find the value of K.
Solution.

Question.22 If the vertices of a triangle are (1, -3), (4, p) and (-9, 7) and its area is 15 sq. units, find the value(s) of p.
Solution.

Question.23 A box contains 100 red cards, 200 yellow cards and 50 blue cards. If a card is drawn at random from the box, then find the probability that it will be
(i) a blue card
(ii) not a yellow card
(iii) neither yellow nor a blue card.
Solution.

Question.24 The 17th term of an AP is 5 more than twice its 8th term. If the 11th term of the AP is 43, then find its nth term.
Solution.

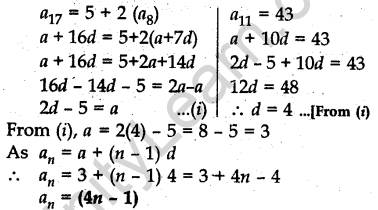
Question. 25 A shopkeeper buys some books for Rs80. If he had bought 4 more books for the same amount, each book would have cost Rs 1 less. Find the number of books he bought.
Or
The sum of two numbers is 9 and the sum of their reciprocals is 1/2. Find the numbers.
Solution.

Question.26 Sum of the first 14 terms of an AP is 1505 and its first term is 10. Find its 25^th term.
Solution.

Question.27 Prove that the tangent at any point of a circle is perpendicular to the radius through the point of contact.
Or
A quadrilateral ABCD is drawn to circumscribe a circle. Prove that AB + CD = AD + BC.
Solution.

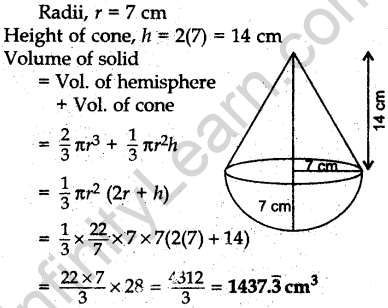
Question.28 A solid is in the shape of a cone surmounted on a hemisphere, the radius of each of them being 3.5 cm and the total height of solid is 9.5 cm. Find the volume of the solid.
[Use π = 22/7 ]
Solution.

Question.29 A bucket is in the form of a frustum of a cone and it can hold 28.49 litres of water. If the radii of its circular ends are 28 cm and 21 cm, find the height of the bucket.
[Use π = 22/7 ]
Solution.

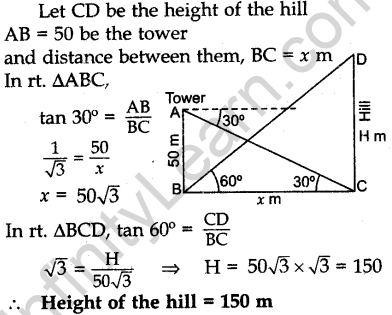
Question.30 The angle of elevation of the top of a hill at the foot of a tower is 60° and the angle of depression from the top of the tower of the foot of the hill is 30°. If the tower is 50 m high, find the height of the hill.
Solution.

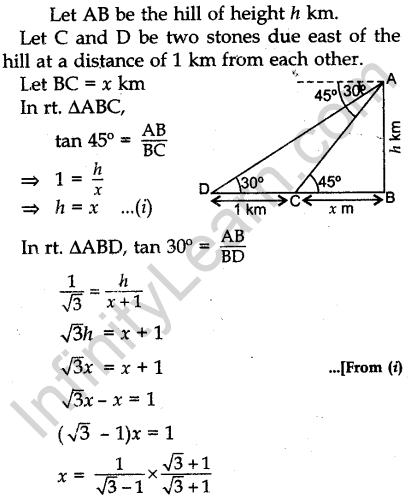
Question.31 From the top of a hill, the angles of depression of two consecutive kilometre stones due east are found to be 30° and 45°. Find the height of the hill.
Solution.

SET II

Note: Except for the following questions, all the remaining questions have been asked in Set-I.
Question.13 Find the value(s) of k so that the quadratic equation 2x² + kx + 3 = 0 has equal roots.
Solution.

Question.14 Find the sum of all three digit natural numbers, which are multiples of 9.
Solution.

Question. 21 A box contains 35 blue, 25 white and 40 red marbles. If a marble is drawn at random from the box, find the probability that the drawn marble is
(i) white
(ii) not blue
(iii) neither white nor blue.
Solution.

Question.22 The 15th term of an AP is 3 more than twice its 7th term. If the 10th term of the AP is 41, then find its n^th term.
Solution.

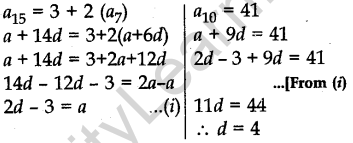
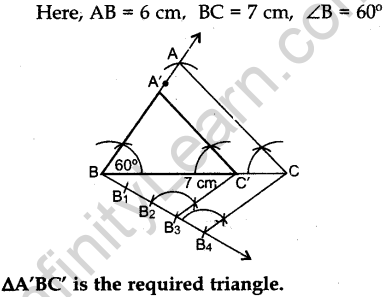
Question.23 Draw a triangle ABC with side BC = 7 cm, ∠ABC = 60° and AB = 6 cm. Then construct
another triangle whose sides are 3/4 times the corresponding sides of ΔABC.
Solution.

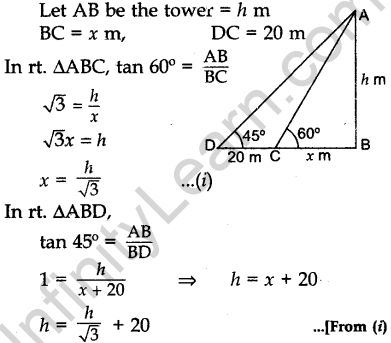
Question.24 The shadow of a tower standing on a level ground is found to be 20 m longer when the Sun’s altitude is 45° than when it is 60°. Find the height of the tower.
Solution.

Question.29 The sum of the first 15 terms of an AP is 750 and its first term is 15. Find its 20th term.
Solution.

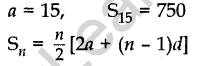
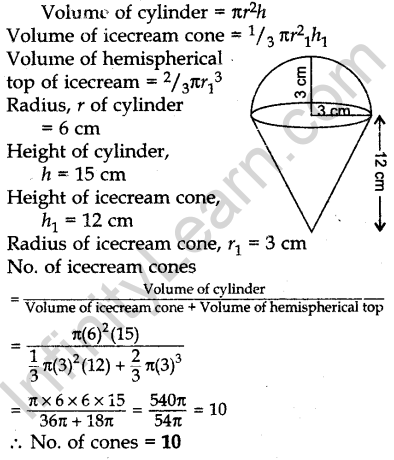
Question.30 A container shaped like a right circular cylinder having base radius 6 cm and height 15 cm is full of ice-cream. The ice-cream is to be filled into cones of height 12 cm and radius 3 cm, having a hemispherical shape on the top. Find the number of such cones which can be filled with ice-cream.
Solution.

SET III

Note: Except for the following questions, all the remaining questions have been asked in Set-I and Set-II.
Question.13 Find the sum of all three digit natural numbers, which are multiples of 7.
Solution.

Question.14 Find the value(s) of k so that the quadratic equation 3x²– 2kx + 12 = 0 has equal roots.
Solution.

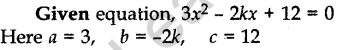
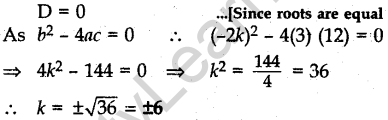
Question.21 A kite is flying at a height of 45 m above the ground. The string attached to the kite is temporarily tied to a point on the ground. The inclination of the string with the ground is 60°. Find the length of the string assuming that there is no slack in the string.
Solution.

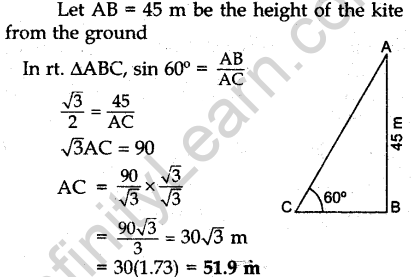
Question.22 Draw a triangle ABC with side BC = 6 cm, ∠C = 30° and ∠A = 105°. Then construct another
triangle whose sides are 2/3 times the corresponding sides of ΔABC.
Solution.

Question.23 The 16th term of an AP is 1 more than twice its 8th term. If the 12th term of the AP is 47, then find its nth term.
Solution.

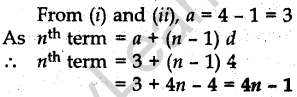
Question.24 A card is drawn from a well shuffled deck of 52 cards. Find the probability of getting
(i) a king of red colour
(ii) a face card
(iii) the queen of diamonds.
Solution.

Question.29 Sum of the first 20 terms of an AP is -240, and its first term is 7. Find its 24th term.
Solution.

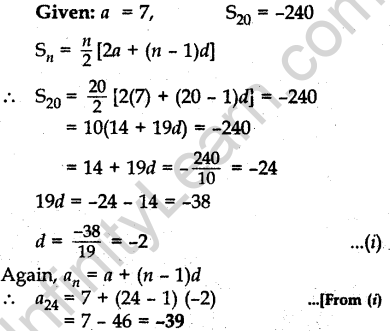
Question.30 A solid is in the shape of a cone standing on a hemisphere with both their radii being equal to 7 cm and the height of the cone is equal to its diameter. Find the volume of the solid.
[Use π = 22/7]
Solution.