Table of Contents
Triangle Formula
What is the Perimeter of a triangle?
The Perimeter of a triangle is the total length around the triangle. Consider a triangle with sides of lengths ‘a’, ‘b’, and ‘c’.
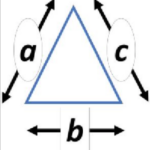
Thus, the perimeter of the triangle = a + b + c.
What is the Base and Height of a triangle?
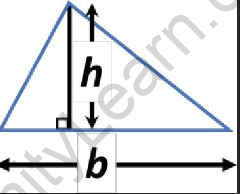
The Base of a triangle is the side on which the triangle rests. Any one of the three sides of the triangle can be considered as the base.
The perpendicular drawn from a base to the opposite vertex of a triangle is known as the corresponding Height of the triangle.
Triangles with different bases and corresponding heights
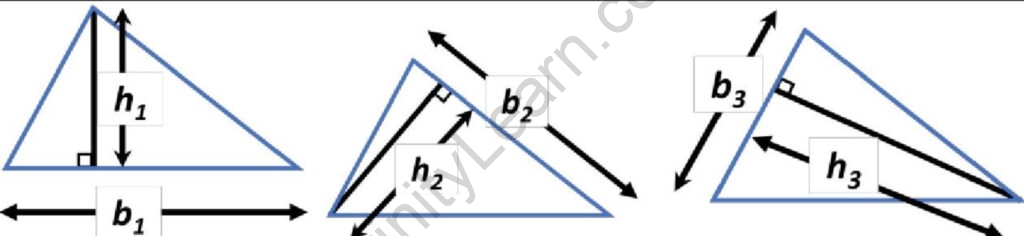
For the above triangles, ℎ1 is the corresponding height of base b1, ℎ2 is the corresponding height of base b2, ℎ3 is the corresponding height of base b3.
Question: What is the Area of a triangle?
- To find the area of the triangle, a base and its corresponding height are considered. Consider a triangle with base ‘b’ and corresponding height ‘h’.
Then, the area of the triangle = 1/2× b × ℎ
That is, area of a triangle is ½ times the product of its base and the corresponding height.
If the height and base of a triangle is not given and the lengths of all three sides of the triangle are known, Heron’s formula can be used to calculate the area. Heron’s formula is a general formula for calculating the area of any triangle using the lengths of its sides.
Heron’s Formula:
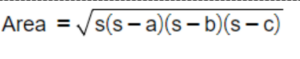
How is the formula to find the area of a triangle obtained?
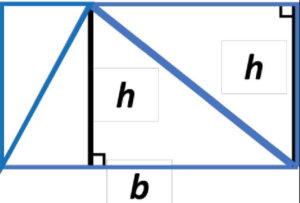
Consider a triangle as shown below.

If the base and the corresponding height of this triangle are b and h respectively, then the area of this triangle is 1/2× b × ℎ. Let us verify this using the following steps.
Step 1: Consider a copy of the same triangle along with the original one.
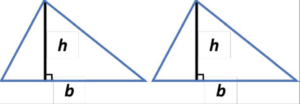
Since, both the triangles are congruent, they will have the same area.
Step 2: The second triangle is flipped horizontally and then vertically, it will be as shown below.
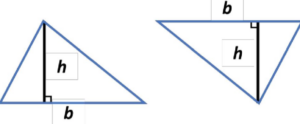
Step 3: Combining these two triangles, we give us a quadrilateral as shown below.
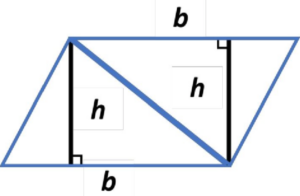
The area of this quadrilateral will be the sum of the areas of the two triangles. But areas of both the triangles are the same.
So, Area of the quadrilateral = 2 x Area of a triangle. … (i)
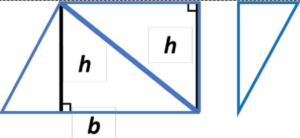
Step 4: Now, the quadrilateral is fragmented as shown below.
Step 5: We will rearrange the fragmented portion to get a rectangle as shown below,
Here, the length of the rectangle is b and the breadth of the rectangle is h.
 A
A
rea of rectangle = L x B
So, area of rectangle = b x h …. (ii)
Also, the area of the rectangle = area of the quadrilateral from step 3 ….. (iii)
From (i), (ii), and (iii),
2 x Area of triangle = b x h
Hence, Area of triangle =1/2× b × ℎ
Solved Examples on Triangle Formulae:
Example 1. If the base and the corresponding height of a triangle is 10 cm and 4 cm respectively, then its area is given by,
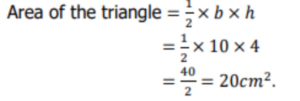
So, the area of the triangle is 20𝑐𝑚2.
Example 2. If the sides of a triangle are 13 cm, 10 cm, and 5 cm, then its perimeter is given by, Perimeter of the triangle = a + b + c
= 13 + 10 + 5
= 28 cm.
So, the perimeter of the triangle is 28 cm.
Learn More Formulas:
Frequently asked questions on Triangle Formulae:
What are the main formulas used to calculate the area of a triangle?
The main formulas to calculate the area of a triangle depend on the given information. For a triangle with base 'b' and height 'h', the formula is Area = (1/2) * b * h. If the lengths of the three sides of the triangle are known, you can use Heron's formula: Area = √(s * (s - a) * (s - b) * (s - c)), where 's' is the semi-perimeter and 'a', 'b', and 'c' are the lengths of the sides.
How can I find the length of an unknown side in a triangle?
To find the length of an unknown side in a triangle, you can use various formulas, such as the Pythagorean Theorem for right triangles or the law of cosines for non-right triangles. The specific formula used depends on the information given, such as the lengths of other sides and angles of the triangle.
How can I find the angles of a triangle if I know the lengths of its sides?
To find the angles of a triangle when the lengths of its sides are known, you can use the law of cosines or the law of sines. The law of cosines is applicable to all triangles, while the law of sines is specifically useful for solving triangles that are not right triangles.
What is the perimeter of a triangle and how do I calculate it?
The perimeter of a triangle is the sum of the lengths of its three sides. To calculate the perimeter, you simply add up the lengths of the three sides.
Can I find the area of a triangle without knowing its height?
Yes, you can find the area of a triangle without knowing its height if you have the lengths of its sides. By using Heron's formula, you can calculate the area based on the lengths of the sides alone, without explicitly needing the height.





