Table of Contents
The wavelength formula is a fundamental equation used in the study of waves and electromagnetic radiation. It relates the wavelength (λ) of a wave to its frequency (f) and the speed of the wave (v). The formula is given as λ = v / f, where λ is the wavelength, v is the speed of the wave, and f is the frequency of the wave. The formula shows that wavelength and frequency are inversely proportional: as the frequency increases, the wavelength decreases, and vice versa. The formula is applicable to various types of waves, including sound waves, light waves, and radio waves, and it provides a quantitative relationship between the different characteristics of a wave.
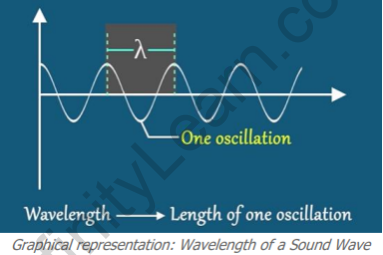
Definition of Wavelength
The distance between the peak value of two consecutive compressions or two consecutive rarefactions is called the wavelength.
It is denoted by → λ.
S.I. unit is meter.
Wavelength Formula
The wavelength formula relates the wavelength of a wave to its speed and frequency. It is expressed mathematically as:
Wavelength (λ) = Speed of the Wave (v) / Frequency (f)
Where:
- Wavelength (λ) is the distance between two consecutive points of the wave in a single cycle, usually measured in meters (m) or other length units.
- Speed of the Wave (v) is the rate at which the wave propagates through a medium, typically measured in meters per second (m/s).
- Frequency (f) is the number of complete cycles or oscillations of the wave that occur in one second, measured in hertz (Hz) or cycles per second.
The wavelength formula shows that wavelength and frequency are inversely proportional to each other. When the frequency of a wave increases, its wavelength decreases, and vice versa. This relationship is consistent with the behavior of waves, where shorter wavelengths correspond to higher frequencies, and longer wavelengths correspond to lower frequencies.
It’s important to note that the wavelength formula applies to various types of waves, including electromagnetic waves (such as light and radio waves) and mechanical waves (such as sound waves). However, the speed of the wave may differ depending on the nature of the wave and the medium through which it propagates.
Understanding the wavelength formula is essential in fields such as physics, optics, acoustics, and telecommunications, as it allows for calculations and predictions regarding the behavior and characteristics of waves.
Solved Examples on Wavelength Formula
Example 1: Calculate the wavelength of a sound wave given its speed and frequency.
Solution:
Speed of the wave (v) = 340 m/s
Frequency (f) = 440 Hz
Using the wavelength formula: Wavelength (λ) = Speed of the Wave (v) / Frequency (f)
Wavelength (λ) = 340 m/s / 440 Hz
Wavelength (λ) ≈ 0.773 m
Therefore, the wavelength of the sound wave is approximately 0.773 meters.
Example 2: Determine the frequency of an electromagnetic wave given its wavelength and speed.
Solution:
Wavelength (λ) = 500 nm
Speed of the wave (v) = 3 × 108 m/s
Converting the wavelength from nanometers (nm) to meters (m):
1 nm = 1 × 10-9 m
Wavelength (λ) = 500 nm × 1 × 10-9 m/nm
Wavelength (λ) = 5 × 10-7 m
Using the wavelength formula: Frequency (f) = Speed of the Wave (v) / Wavelength (λ)
Frequency (f) = 3 × 108 m/s / 5 × 10-7 m
Frequency (f) = 6 × 1014 Hz
Therefore, the frequency of the electromagnetic wave is 6 × 1014 Hz.
Example 3: Calculate the speed of light given its wavelength and frequency.
Solution:
Wavelength (λ) = 500 nm
Frequency (f) = 6 × 1014 Hz
Converting the wavelength from nanometers (nm) to meters (m):
1 nm = 1 × 10-9 m
Wavelength (λ) = 500 nm × 1 × 10-9 m/nm
Wavelength (λ) = 5 × 10-7 m
Using the wavelength formula: Speed of the Wave (v) = Wavelength (λ) × Frequency (f)
Speed of the Wave (v) = 5 × 10-7 m × 6 × 1014 Hz
Speed of the Wave (v) = 3 × 108 m/s
Therefore, the speed of light is approximately 3 × 108 m/s.
Related Formula:
| Refractive Index Formula | Mass Formula |
| Ohms Law Formula | Wavelength Formula |
| Electric Power Formula | Resistivity Formula |
FAQs on Wavelength Formula
What is the wavelength formula?
The wavelength formula relates the wavelength of a wave to its speed and frequency. It is expressed as: Wavelength (λ) = Speed of the Wave (v) / Frequency (f).
What is the unit of wavelength?
The unit of wavelength is typically represented as meters (m). However, in some cases, other units such as nanometers (nm), micrometers (μm), or even kilometers (km) may be used depending on the scale of the wave. The choice of unit depends on the specific application and the range of wavelengths being measured.
What is λ in wavelength formula?
In the wavelength formula, λ represents the symbol for wavelength. It is the distance between two consecutive points in a wave. The unit of wavelength is typically meters (m), and it is inversely related to the frequency of the wave. The wavelength formula, λ = v / f, relates the wavelength to the speed of the wave (v) and its frequency (f).
How do you calculate wavelength?
Wavelength can be calculated by dividing the speed of the wave by its frequency. The formula for calculating wavelength is λ = v / f, where λ represents the wavelength, v is the speed of the wave, and f is the frequency of the wave. By knowing the values of the speed and frequency, you can simply divide the speed by the frequency to obtain the wavelength.
What is the velocity of a wave?
The velocity of a wave is the rate at which the wave propagates through a medium. It refers to the speed and direction of the wave's motion. In the context of waves, velocity is typically measured in meters per second (m/s). The velocity of a wave depends on the properties of the medium through which it is traveling, such as the density and elasticity. It is determined by the product of the wavelength and the frequency of the wave, following the formula v = λ x f.
How is wavelength related to frequency?
Wavelength and frequency are inversely proportional to each other. As the frequency of a wave increases, its wavelength decreases, and vice versa. Mathematically, this relationship is described by the equation: Wavelength (λ) = Speed of the Wave (v) / Frequency (f).
What are the 7 wavelengths?
There are several types of wavelengths in the electromagnetic spectrum. These include radio waves, microwaves, infrared waves, visible light, ultraviolet waves, X-rays, and gamma rays. Each of these wavelengths corresponds to a different range of frequencies and energies. For example, radio waves have long wavelengths and low frequencies, while gamma rays have short wavelengths and high frequencies. These different types of wavelengths have various applications in communication, imaging, and scientific research.
Which is the shortest wavelength?
Among the electromagnetic spectrum, gamma rays have the shortest wavelengths. Gamma rays have wavelengths shorter than X-rays and are associated with high-frequency electromagnetic radiation. They have extremely high energy and are often generated in nuclear reactions or during high-energy particle interactions. Due to their high penetrating power and ionizing nature, gamma rays are used in various applications such as medical imaging, cancer treatment, and industrial radiography.
Can the wavelength formula be used for all types of waves?
Yes, the wavelength formula can be used for various types of waves, including electromagnetic waves (such as light and radio waves) and mechanical waves (such as sound waves). However, the speed of the wave may differ depending on the nature of the wave and the medium through which it propagates.
How is the wavelength of light determined?
The wavelength of light can be determined using various techniques, such as spectroscopy or interference patterns. Instruments like spectrometers or interferometers are commonly used to measure and analyze the wavelengths of light emitted or absorbed by different substances or sources.
Can wavelength be negative?
No, wavelength is a physical quantity that represents a distance or length, and it cannot be negative. Wavelength is always a positive value.







