Acute Angles – Definition, Measurement, Examples, Types and Properties

An Acute Angle is an angle that is smaller than a right angle or a 90° Angle. The polygons such as triangles or trapezoids consist of at least one angle which forms an Acute Angle. In this article, we will learn more about acute angles, their examples, and their properties.

Also Check: Vertices, Faces and Edges

Acute Angles

The two lines when cut through each other or meet each other at a common point forms an angle between them. An angle is denoted by the symbol ∠. Also, an angle is measured using a mathematical tool called Protractor. An angle is measured in degrees (°).

Acute Angles Definition

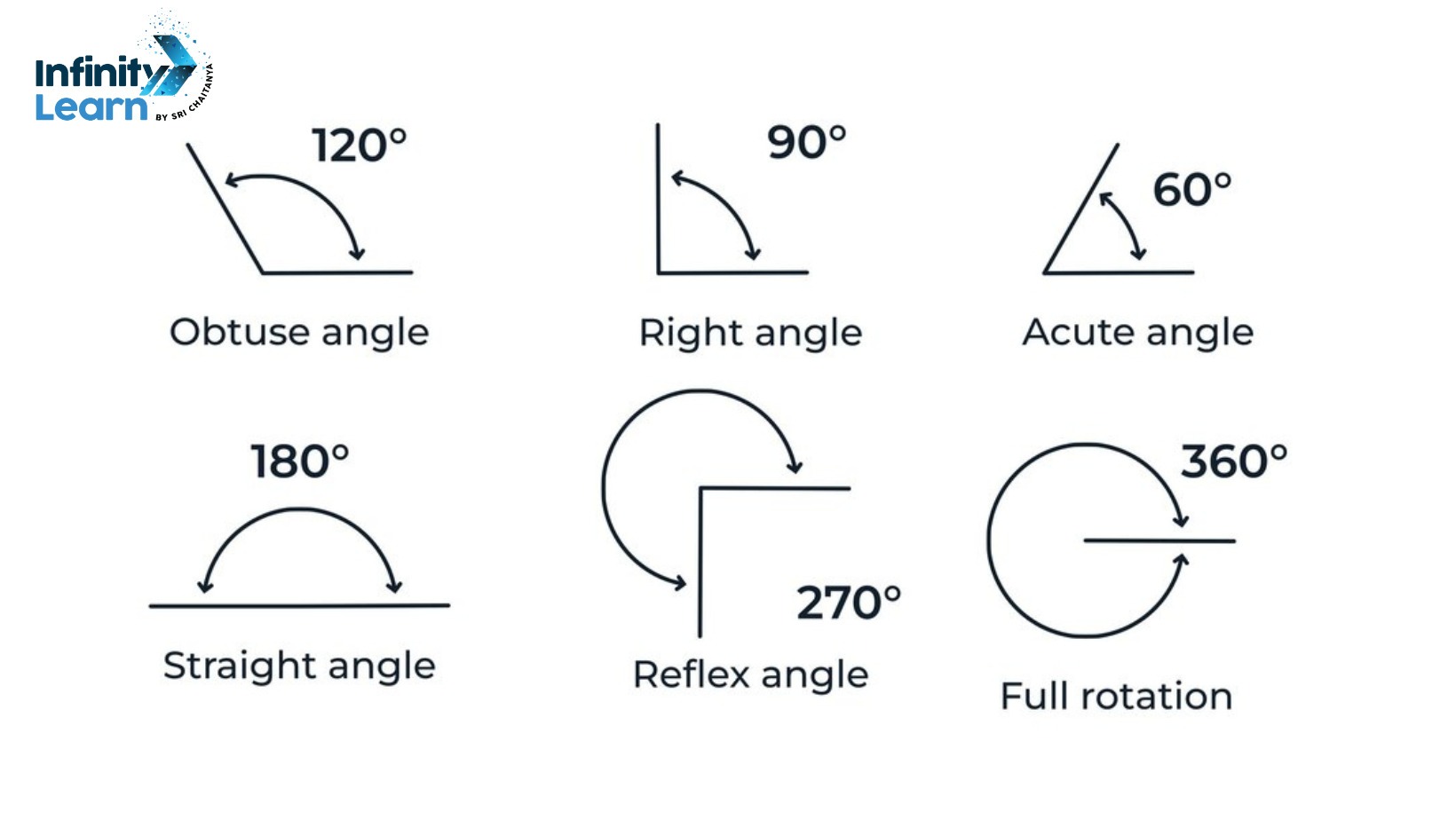
There are three major types of angles.

1. Acute Angles
2. Right Angles (90° angle)
3. Obtuse Angles

The figure below shows the clear difference between all three types of angles.

When you measure an angle and it is less than 90°, then it is said to be an Acute Angle. Therefore, any angle which measures less than a right angle is said to be an acute angle. ∠12° ∠31°, ∠35° and ∠45° are a few examples of Acute Angles.

Also Check: Area of a Circle

Acute Angles Examples

As we know an angle lesser than 90° can be categorized as Acute Angles. Therefore, the examples of Acute Angles include ∠35°, ∠45°, ∠7°, ∠89°, ∠34°, ∠16°, etc.

Understand these examples from the figure below.

∠30° measures less than 90° (the dotted line in the below-given figure represents the right angle), hence it can be categorized as an Acute Angle.

How to measure an Acute Angle?

An Acute Angle can be measured using the Protractor. Follow the mentioned steps to find the angle.

1. Place the center of the Protractor at a fixed point O, which is the point where both the lines making the angle meet.
2. Make sure to coincide the reference line on the Protractor with an arm of the angle at point O. This is the initial line (zero degrees).
3. Another arm of the angle will now indicate the degree of angle formed. You will have to measure it from the initial hand in the anti-clockwise direction.

Acute Angle Degree

The Acute Angle, whenever measured, is less than 90°. It is always less than the right angle. Therefore, the range of acute angle degrees ranges from 0° to 90°. Also, dividing the right angle in any way gives us two or more acute angles. Each angle formed will be less than 90°.

Acute Angle Images

Can two acute angles form a linear pair?

No, two acute angles can not form a linear pair. As we know the measure of a linear pair of angles is 180° and the acute angles always measure less than 90°, therefore, the sum of two acute angles can not give us a linear pair.

For example:

• Let’s assume 87° and 83° are two acute angles. Therefore, their sum is 170° (87+83= 170°) which is not a linear pair.
• 90° + 90° = 180° but the angles are not acute. 90° forms a right angle.
• 95° + 85° = 180° but 95° is an Obtuse Angle. Therefore, two acute angles can not form a linear pair.

Acute Angle Triangle

If all the angles of a triangle measure less than 90°, then the triangles are said to be an acute angle triangle. In the image below an example of an acute angle triangle is shown.

Properties of Acute Angle Triangle

• All equilateral triangles are Acute Angle Triangle.
• All the angles of the equilateral triangles measure equal to 60°.
• The side opposite to the highest measuring angle is the largest.
• Acute angle triangles can be Equilateral, Isosceles or scalene triangles.

Acute Angles in Real Life

• The angle made while writing the alphabet V is an acute angle.
• If we slice a pizza into more than 4 slices then the angle made by each slice at the center is an acute angle.
• The hands of the clock make acute angles several times a day. For example when the clock strikes 2:00 in the watch.
• The road signs have acute angles hidden in them.
• The speedometer of the vehicles makes acute angles as well.

Acute Angle Formula

In an acute triangle, the following statements hold true.

1. a² + b² > c²
2. b² + c² > a²
3. c² + a² > b²

Where, a, b, and c are the sides of the triangle.

Acute Angle Examples

1. 1. If a given angle (x) is acute then verify if x is acute if it measures as:

• 20°

• 60°

• 110°

• 105°

• 176°

Ans. If the given angle x is acute, then:

1. 20° < 90°, therefore, x is an acute angle if x = 20°.
2. 60° < 90°, therefore, x is an acute angle if x = 60°.
3. 110° > 90°, therefore, x is not an acute angle if x = 110°.
4. 105° > 90°, therefore, x is not an acute angle if x = 105°.
5. 176° > 90°, therefore, x is not an acute angle if x = 176°

2. 2. Which angle is an Acute Angle?

Ans. Option A i.e. ∠30 is an acute angle.

Acute Angles and Obtuse Angle

Acute Angle: The angle whose measure is less than 90° is said to be an acute angle.

Obtuse Angle: The angle that measures more than a right angle or 90° angle is said to be an Obtuse Angle.

Acute Angle	Obtuse Angle
Measure of the Acute Angle is always less than 90°.	The Measurement of the Obtuse Angle is between 90° and 180°.
A triangle can have more than one acute angle.	A triangle can not have more than one Obtuse Angle..
An acute angle always measures less than a right angle.	An Obtuse Angle is greater than a right angle but less than a straight angle.

Acute Angle: FAQs

What are the acute angles?

An acute angle is defined as an angle which measures less than a right angle. For example: 70°, 45°, and 56°. These all angles are less than the right angle or a 90° angle. Therefore, they are acute angles.

Is 0° an acute angle?

Yes, 0° is an acute angle. It is also called a zero angle.

Is 45° an acute angle?

Yes, 45° is an acute angle as it measures less than 90°. Therefore, as per the definition of acute angles, it is categorized as an acute angle.