Table of Contents
A diagonal is an important concept in geometry. A diagonal is a line segment connecting two non-adjacent vertices of a polygon. Diagonals help in dividing polygons into smaller triangles, calculating areas, and understanding the internal structure of shapes. This article will discuss the diagonal, its meaning and more.
Diagonal Definition
A diagonal is a line segment that connects any two non-adjacent vertices of a polygon. It is different from the sides of the polygon because sides always connect adjacent vertices. To draw a diagonal, pick any vertex of the polygon and connect it to another vertex that is not directly adjacent to it. This will form a diagonal.
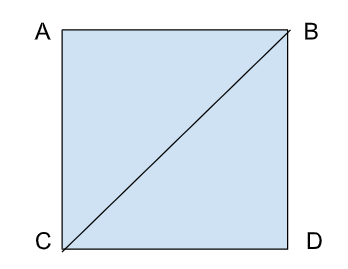
Here, ABDC is a polygon and BC is a diagonal of the given polygon.
Examples of Diagonals
Below given are a few examples of diagonals.
Diagonals in a Triangle
A triangle has no diagonals because every vertex is connected to the other two vertices by sides.
Diagonals in a Quadrilateral
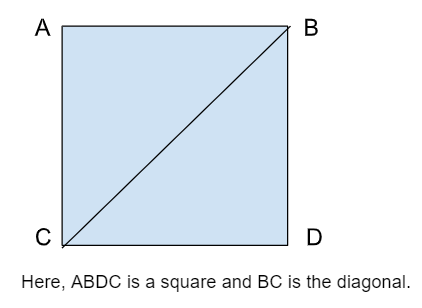
A quadrilateral, like a square or rectangle, has two diagonals. These diagonals can divide the shape into four right triangles or two congruent triangles.
Applications of Diagonals
Below given are a few applications of diagonals.
- Diagonals are used in dividing polygons into smaller, manageable shapes, making it easier to calculate areas and understand the internal angles.
- Diagonals are also used in architectures. It helps in designing stable structures, such as beams in buildings, where the diagonal supports help distribute weight.
- Diagonals are used in perspective drawing to create depth and dimension.
Diagonals Formulas
To find the number of diagonals in a polygon, we can use the below given formula.
Number of diagonals = n(n-3)/2
where n represents the number of vertices (or sides) of the polygon.
For Example: Calculating Diagonals of a Square
To calculate the number of diagoals of square, which has 4 vertices, we use n = 4 in the above-mentioned formula.
Therefore,
Number of diagonals = 4 (4 – 3)/2
Number of diagonals = 4 (1)/2
Number of diagonals = 2
Therefore, the number of diagonals of the square is equal to 2.
So, the square has 2 diagonals.
General Examples
This formula can be applied to any polygon to find the number of diagonals. For example:
- A triangle has no diagonals.
- A pentagon has 5 diagonals.
Diagonals of Shapes
Diagonals play an important role in the geometry of different shapes. Below discussed are the diagonals of various common shapes.
1. Diagonals of a Triangle
A triangle is a polygon which has three sides and three vertices. A diagonal is defined as a line segment connecting two non-adjacent vertices, and a triangle has no such non-adjacent vertices. Therefore, a triangle does not have any diagonals.
Number of Diagonals in a Triangle: 0
2. Diagonals of a Square
A square has four sides and four vertices. The diagonals of a square connect opposite vertices and have several important properties:
- A square has 2 diagonals.
- The diagonals are congruent. It means that both the diagonals are equal in length.
- The diagonals bisect each other at right angles (90 degrees).
- Each diagonal divides the square into two congruent isosceles and right triangles.
3. Diagonals of a Rectangle
Similar to a square, a rectangle has four sides and four vertices. The diagonals of a rectangle also connect opposite vertices and share similar properties with those of a square:
- A rectangle has 2 diagonals.
- The diagonals are congruent.
- The diagonals of a rectangle bisect each other. They divide the rectangle into two congruent right triangles.
4. Diagonals of a Rhombus
A rhombus is a four-sided polygon (quadrilateral) where all sides have equal length. The diagonals of a rhombus have unique properties:
- A rhombus has 2 diagonals.
- The diagonals bisect each other at right angles.
- The diagonals are not congruent, unlike in a square or rectangle.
- The diagonals divide the rhombus into four right triangles.
5. Diagonals of a Parallelogram
A parallelogram is a polygon with four sides. All the opposite sides of a parallelogram are parallel and equal in length. The diagonals of a parallelogram also have distinct properties:
- A parallelogram has 2 diagonals.
- The diagonals bisect each other but are not necessarily congruent.
- They divide the parallelogram into two congruent triangles.
6. Diagonals of a Pentagon
A pentagon is a polygon with five vertices and five sides. Below given are the properties of the diagonals of a pentagon.
- A pentagon has 5 diagonals.
- These diagonals connect non-adjacent vertices, creating various internal shapes within the pentagon.
7. Diagonals of a Hexagon
A hexagon is a six-sided polygon with six vertices. The number of diagonals in a hexagon increases as the number of sides increases.
- A hexagon has 9 diagonals.
- These diagonals connect non-adjacent vertices, forming various internal triangles and other polygons.
8. Diagonals of a Cube
A cube is a three-dimensional shape with six square faces, eight vertices, and twelve edges. Diagonals in a cube are categorized as face diagonals and space diagonals:
- Face Diagonals: Each square face of the cube has 2 diagonals.
- Space Diagonals: A space diagonal passes through the interior of the cube, connecting opposite vertices. A cube has 4 space diagonals.
9. Diagonals of a Cuboid
A cuboid is a three-dimensional shape with rectangular faces. It has face diagonals and space diagonals similar to a cube.
- Face Diagonals: Each rectangular face of the cuboid has 2 diagonals.
- Space Diagonals: There are 4 space diagonals connecting opposite vertices.
Number of Diagonals in Polygons
We know that the formula to calculate the number of diagonals in a polygon is given by:
Number of diagonals = n (n – 3)/2
where n is the number of vertices in the polygon.
Below given table gives us the data for different shapes.
| Polygon | Number of Vertices (n) | Calculation | Number of Diagonals |
| Triangle | 3 | 3 (3 – 3)/2 | 0 |
| Quadrilateral | 4 | 4 (4 – 3)/2 | 2 |
| Pentagon | 5 | 5 (5 – 3)/2 | 5 |
| Hexagon | 6 | 6 (6 – 3)/2 | 9 |
| Heptagon | 7 | 7 (7 – 3)/2 | 14 |
| Octagon | 8 | 8 (8 – 3)/2 | 20 |
| Nonagon | 9 | 9 (9 – 3)/2 | 27 |
| Decagon | 10 | 10 (10 – 3)/2 | 35 |
FAQs on Diagonals
What is a diagonal?
A diagonal is a straight line that connects two non-adjacent vertices (corners) of a polygon, cutting across the shape.
How many diagonals does a heptagon have?
A heptagon is a shape which has 7 vertices. It has 14 diagonals.
Does a circle have a diagonal?
No, a circle does not have a diagonal because it does not have vertices or sides.








