Table of Contents
A parallelogram is a polygon that has a two-dimensional geometrical shape. A parallelogram has four sides. The sides of a parallelogram are parallel to each other. Parallel sides have equal lengths in a parallelogram. If we add the adjacent angles of a parallelogram, the sum is equal to 180⁰.
In this article, we will study about shape of parallelograms, angles of parallelograms, properties of parallelogram, area and perimeter of parallelograms, and parallelogram theorems.
Parallelogram Definition
A parallelogram has two pairs of parallel lines. It is a quadrilateral in which opposite sides are equal in length. Opposite angles of a parallelogram are also equal when measured. The sum of all the interior angles of a parallelogram equals 360⁰.
In a parallelogram, interior angles of the same side of a transversal are supplementary.
Below given is the figure of a parallelogram:
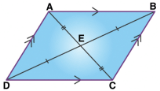
Here, ABCD is a parallelogram.
AB || CD and AD || BC.
AB = CD and AD = BC.
And ∠A = ∠C and ∠B = ∠D.
∠A and ∠D are supplementary angles as these interior angles are lying on the same side of the transversal. Same, ∠ B and ∠C are supplementary angles.
Therefore,
∠A + ∠D = 180
∠ B + ∠C = 180
Also Check: Parallelogram Formula
Shape of Parallelogram
A parallelogram has a two dimensional shape. It has four sides in which two pairs of sides are parallel and equal. In case, if the length of the two sides are not equal, that shape will not be considered as a parallelogram. The opposite interior angles of a parallelogram should also be equal, of they are not equal, it will not be a parallelogram.
Angles of Parallelogram
A parallelogram is a two dimensional shape having four angles. In a parallelogram, opposite interior angles are equal. The angels which are present on the same sides of the transversal are supplementary. The sum of the interior angles of a parallelogram is 360⁰.
Area of Parallelogram
The region occupied by a parallelogram in a two-dimensional plane is the area of a parallelogram. Below discussed is the formula to find the area of a parallelogram:
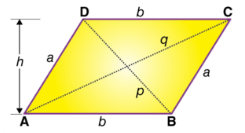
Area = Base × Height
In the above parallelogram, ABCD, the area is given by:
Area = ab sin A = ba sin B
Where a is the slant length of the side of a parallelogram and b is the base
Do Check: Diagonal of Parallelogram Formula
Perimeter of Parallelogram
The perimeter of a parallelogram can be calculated as the total length of the distance of the boundaries of the parallelogram. The values of length and breadth should be known to calculate the perimeter of the parallelogram. The opposite sides of a parallelogram when measured, are equal. The formula used to calculate the perimeter of a parallelogram is as follows:
Perimeter = 2 (a+b) units , where a and b are the lengths of the sides of a parallelogram.
Properties of Parallelogram
The properties of a parallelogram are written below:
- The opposite sides of a parallelogram are equal and parallel as well as the opposite angles are also equal.
- The adjacent angles are also equal.
- In a parallelogram, if any one angle is right angle, then all the other angles will also be right angle.
- The two diagonals of a parallelogram bisect each other.
- The two diagonals bisect the parallelogram into two congruent triangles.
- In a parallelogram, the sum of the square of all the sides is equal to the sum of the square of its diagonals.
Parallelogram Theorems
Theorem 1: Parallelograms that are present on the same base and between the same parallel sides are equal in area.
Proof: Two parallelograms ABCD and ABEF are on the same base DC and are between the same parallel lines AB and FC.
To prove area of ABCD = area of ABEF.
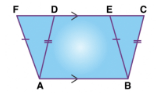
In ∆ADF and ∆BCE,
AD = BC and AF = BE. ( ABCD and ABEF are parallelograms).
∠ADF = ∠BCE (corresponding angles)
∠AFD = ∠BEC (corresponding angles)
∠DAF = ∠CBE (corresponding angles)
Therefore, ∆ADE ≈ ∆BCF (SAS rule)
Area ∆ ADF = Area ∆ BCE (By congruence area axiom)
Area(ABCD) = Area(ABED) + Area(BCE)
Area(ABCD) = Area(ABED)+Area(ADF)
Area(ABCD) = Area(ABEF)
Hence, Parallelograms that are present on the same base and between the same parallel sides are equal in area.
Also Check: Area of Parallelogram
Theorem 2: The area of a parallelogram is the result of the product of its base and the corresponding altitude.
Given: AB is the base in a parallelogram ABCD.
To prove: Area of Parallelogram = AB × AL
Construction: Draw a BM perpendicular to CD.
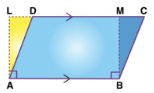
In the given figure, the base of the rectangle ABCD and rectangle ABML are the same. They are also between the same parallel lines AB and LC.
Area of Parallelogram ABCD = Area of Parallelogram ABML.
Area of rectangle = length × breadth
Area of Parallelogram ABCD = AB × AL
Therefore, the area of a parallelogram is the result of the product of its base and the corresponding altitude.
Also Check: Perimeter of a Parallelogram Formula
Difference between Parallelogram and Rhombus
| Parallelogram | Rhombus |
| A parallelogram is a quadrilateral. It’s opposite sides are both equal and parallel. | A rhombus is a quadrilateral. All the sides are congruent in it. |
| The diagonals of a parallelogram bisect each other. | The diagonals of a rhombus bisect each other at a right angle. |
| In a parallelogram, opposite angles are equal. | In a rhombus, opposite angles are equal. |
FAQs on Parallelogram
Define Parallelogram
A parallelogram is a polygon which has a two dimensional geometrical shape. The sides of a parallelogram are parallel to each other. A parallelogram has four sides. Parallel sides have equal length in a parallelogram. If we add the adjacent angles of a parallelogram, the sum is equal to 180⁰.
Give some examples of a parallelogram.
A parallelogram has two pairs of parallel lines. It is a quadrilateral in which opposite sides are equal in length. In a parallelogram, opposite angles are equal. The sum of all the interior angles of a parallelogram equals 360⁰
Write some of the properties of a parallelogram.
Some of the properties of a parallelogram are: The opposite sides of a parallelogram are equal and parallel as well as the opposite angles are also equal. The adjacent angles are equal. In a parallelogram, if any one angle is right angle, then all the other angles will also be right angle. The two diagonals of a parallelogram bisect each other. The two diagonals bisect the parallelogram into two congruent triangles









