Trapezoid 

A trapezoid is a geometrical shape. A trapezoid (or trapezium) is a type of quadrilateral that has four sides. A trapezoid is a unique quadrilateral as it only has one pair of opposite sides that are parallel. This characteristic sets it apart from other quadrilaterals, like rectangles and parallelograms, which have two pairs of parallel sides. Read this article to learn more about trapezoids.

Properties of a Trapezoid

Trapezoids have several unique properties that distinguish them from other quadrilaterals. Below-given are some major properties of Trapezoids:

• A trapezoid has one pair of parallel opposite sides and these are called the bases of the trapezoid.
• The other two non-parallel sides are known as the legs or lateral sides of the trapezoid.
• The shortest distance between the two parallel bases is known as the altitude or height of the trapezoid.
• Calculating the area of a trapezoid is straightforward due to its parallel sides. The formula to find the area is Area = 1/2 × ( Base ₁ + Base₂ ) × Altitude

where Base₁ and Base₂ are the lengths of the parallel sides, and Altitude is the perpendicular distance between them.

1. In an isosceles trapezoid, the non-parallel sides (legs) are of equal length. Additionally, the angles adjacent to each base are supplementary, meaning they add up to 180°.
2. The sum of the interior angles next to each other on the same side of the trapezoid is always 180°.
3. The median of a trapezoid is a line segment that connects the midpoints of the non-parallel sides. It is parallel to both bases and its length is the average of the lengths of the two bases: Base ₁ + Base₂.
4. Special Cases:

• If both pairs of opposite sides are parallel and of equal length, the trapezoid is a parallelogram.
• If both pairs of opposite sides are parallel, all sides are of equal length, and all angles are right angles, the trapezoid can be classified as a square.
• If both pairs of opposite sides are parallel, the opposite sides are of equal length, and all angles are right angles, the trapezoid can be classified as a rectangle.

Types of Trapezoids

Trapezoids come in different varieties, each with its own unique properties. Below given are the three main types of trapezoids:

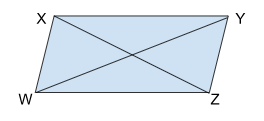
Isosceles Trapezoid

An isosceles trapezoid has equal-length non-parallel sides, known as the legs. This type of trapezoid has a few distinctive features:

• The angles adjacent to each base are equal.
• It has a line of symmetry that divides it into two mirror-image halves.
• Both diagonals are of equal length.

For example, in an isosceles trapezoid XYZW, the bases are XY and WZ, while WX and YZ are the legs.

Scalene Trapezoid

A scalene trapezoid is characterized by having all sides and angles of different lengths and measures. In this type:

• None of the sides are equal.
• The angles adjacent to each base are not necessarily equal.

For example, in a scalene trapezoid with sides AB, BC, CD, and DA, all four sides are of different lengths, and the bases DC and AB are parallel but of different lengths.

Right Trapezoid

A right trapezoid (or right-angled trapezoid) includes one pair of right angles. This type is often used in various applications, including estimating areas under curves. Important features of right-angled trapezoid include:

• One pair of angles is 90 degrees.
• The bases of the trapezoid are parallel.
• In a right trapezoid, such as the one with right angles at points D and A, the bases DC and AB are parallel.

Trapezoid Formulas

Trapezoids have two main formulas used to calculate their area and perimeter. These formulas are given below:

Area of a Trapezoid

To calculate the area of a trapezoid, you need to know the measurements of the lengths of the two parallel sides (bases) and the height (the perpendicular distance between the bases). The formula for the area A is: Area = 1/2 × ( Base ₁ + Base₂ ) × Altitude

where Base1 and Base2 are the lengths of the parallel sides, and Altitude is the perpendicular distance between them.

The area of the trapezoids represents the number of square units that can fit inside the trapezoid. It is measured in square units such as square centimeters (cm²), square meters (m²), or square inches (in²).

Perimeter of a Trapezoid

The perimeter P of a trapezoid is calculated by adding the lengths of all four sides. If the lengths of the non-parallel sides (legs) are c and d, and the lengths of the parallel sides (bases) are a and b, then: Perimeter = a + b + c + d

Solved Examples: Trapezoid

Example 1: Find the area of a trapezoid with bases of 8 cm and 12 cm and a height of 5 cm.

Solution: To find the area of a trapezoid we use the area formula: Area = 1/2 × ( Base ₁ + Base₂ ) × Altitude

The given values for bases and attitude are:

Base1 = 8 cm (shorter base)

Base2 = 12 cm (longer base)

Altitude = 5 cm (height)

Therefore, Area = 1/2 × ( Base 1 + Base2 ) × Altitude

Area = 1/2 × ( 8 + 12 ) × 5

Area = 1/2 × ( 20 ) × 5 = 10 5 = 50

Answer: The area of the trapezoid is 50 cm².

Example 2: A trapezoid has sides measuring 7 m, 9 m, 6 m, and 8 m. Find its perimeter.

Solution: To find the perimeter of a trapezoid we use the perimeter formula: Perimeter = a + b + c + d, where a, b, c, and d are the sides of the given quadilateral figure.

We are given that a=7 m

b=9 m

c=6 m

d=8 m

Therefore, Perimeter = a + b + c + d

Perimeter = 7 + 9 + 6 + 8 = 30

Answer: The perimeter of the trapezoid is 30 m.

Example 3: Find the area and perimeter of a trapezoid with bases of 10 cm and 14 cm, height 6 cm, and non-parallel sides of 5 cm and 7 cm.

Solution: To find the area of a trapezoid we use the area formula: Area = 1/2 × ( Base 1 + Base2 ) × Altitude

We know that:

Base1 = 10 cm (shorter base)

Base2 = 14 cm (longer base)

Altitude = 6 cm

Therefore, Area = 1/2 × ( 10 + 14 ) × 6

Area = 1/2 × ( 24 ) × 6 = 1/2 × 6 = 72

To find the perimeter of a trapezoid we use the perimeter formula: Perimeter = a + b + c + d, where a, b, c, and d are the sides of the given quadilateral figure.

We are given that a=10 cm

b=14 cm

c=5 cm

d=7 cm

Therefore, Perimeter = a + b + c + d

Perimeter = 10 + 14 + 5 + 7 = 36 cm

Answer: The area of the trapezoid is 72 cm², and the perimeter is 36 cm.

Practice Questions

• Find the area of a trapezoid with bases measuring 15 cm and 20 cm and a height of 8 cm.
• A trapezoid has sides of lengths 12 m, 8 m, 5 m, and 10 m. Calculate the perimeter of the trapezoid.
• The bases of a trapezoid are 9 inches and 13 inches, and the height is 7 inches. What is the area of the trapezoid?
• Find the area and perimeter of a trapezoid with bases of 11 cm and 17 cm, a height of 6 cm, and legs of 7 cm and 9 cm.
• A trapezoid has bases of 18 cm and 22 cm, with non-parallel sides measuring 10 cm and 12 cm. What is the perimeter of the trapezoid?
• Calculate the area of a trapezoid where the shorter base is 5 m, the longer base is 9 m, and the height is 4 m.
• A trapezoid has a shorter base of 7 cm, a longer base of 14 cm, a height of 5 cm, and side lengths of 8 cm and 6 cm. Find its area and perimeter.
• Find the area of a trapezoid with parallel sides measuring 25 inches and 15 inches, and a height of 10 inches.

FAQs on Trapezoid

What is the main difference between a trapezoid and other quadrilaterals?

The main difference is that a trapezoid has only one pair of parallel sides, unlike parallelograms or rectangles, which have two pairs of parallel sides.

How do you calculate the area of a trapezoid?

The area of a trapezoid is calculated using the formula: Area = 1/2 × ( Base 1 + Base2 ) × Altitude, where a and b are the lengths of the parallel sides, and h is the height.

Can a trapezoid be classified as a parallelogram?

No, a trapezoid cannot be classified as a parallelogram because it has only one pair of parallel sides, while parallelograms have two pairs of parallel sides.