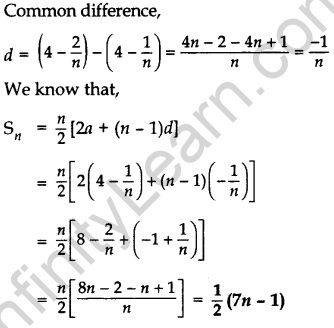Important Questions for Class 10 Maths Chapter 5: Arithmetic Progression

Arithmetic Progressions Class 10 Important Questions Very Short Answer (1 Mark)

Question 1. Find the common difference of the AP \(\frac{1}{p}, \frac{1-p}{p}, \frac{1-2 p}{p}, \dots\). (2013D)
Solution: The common difference,

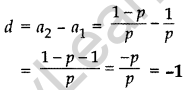
Question 2. Find the common difference of the A.P. \(\frac{1}{2 b}, \frac{1-6 b}{2 b}, \frac{1-12 b}{2 b}, \ldots\). (2013D)
Solution: The common difference, d = a₂ – a₁ = \(\frac{1-6 b}{2 b}-\frac{1}{2 b}\)
= \(\frac{1-6 b-1}{2 b}=\frac{-6 b}{2 b}\) = -3

Question 3. Find the common difference of the A.P. \(\frac{1}{3 q}, \frac{1-6 q}{3 q}, \frac{1-12 q}{3 q}, \dots\). (2013D)
Solution: Common difference, d = a₂ – a₁ = \(\frac{1-6 q}{3 q}-\frac{1}{3 q}\)
= \(\frac{1-6 q-1}{3 q}=\frac{-6 q}{3 q}\) = -2

Question 4. Calculate the common difference of the A.P. \(\frac{1}{b}, \frac{3-b}{3 b}, \frac{3-2 b}{3 b}, \dots\). (2013D)
Solution:
Common difference, d = a₂ – a₁= \(\frac{3-b}{3 b}-\frac{1}{b}\)
= \(\frac{3-b-3}{3 b}=\frac{-b}{3 b}=\frac{-1}{3}\)

Question 5. Calculate the common difference of the A.P. \(\frac{1}{3}, \frac{1-3 b}{3}, \frac{1-6 b}{3}, \dots\) (2013OD)
Solution:
Common difference, d = a₂ – a₁ = \(\frac{1-3 b}{3}-\frac{1}{3}\)
= \(\frac{1-3 b-1}{3}=\frac{-3 b}{3}\) = -b

Question 6. What is the common difference of an A.P. in which a₂₁ – a₇ = 84? (2017OD )
Solution:
a₂₁ – a₇ = 84 …[Given
∴ (a + 20d) – (a + 6d) = 84 …[a_n = a + (n – 1)d
20d – 6d = 84
14d = 84 ⇒ d \(\frac{84}{14}\) = 6

Question 7. Find the 9th term from the end (towards the first term) of the A.P. 5,9,13, …, 185. (2016D)
Solution: Here First term, a = 5
Common difference, d = 9 – 5 = 4
Last term, 1 = 185
n^th term from the end = l – (n – 1)d
9^th term from the end = 185 – (9 – 1)4
= 185 – 8 × 4 = 185 – 32 = 153

Also Check: Important Questions for Class 10 Maths Chapter 1 – Real Numbers

Arithmetic Progressions Class 10 Important Questions Short Answer-I (2 Marks)

Question 8. The angles of a triangle are in A.P., the least being half the greatest. Find the angles. (2011D)
Solution:
Let the angles be a – d, a, a + d; a > 0, d > 0
∵ Sum of angles = 180°
∴ a – d + a + a + d = 180°
⇒ 3a = 180° ∴ a = 60° …(i)
By the given condition
a – d = \(\frac{a+d}{2}\)
⇒ 2 = 2a – 2d = a + d
⇒ 2a – a = d + 2d ⇒ a = 3d
⇒ d = \(\frac{a}{3}=\frac{60^{\circ}}{3}\) = 20° … [From (i)
∴ Angles are: 60° – 20°, 60°, 60° + 20°
i.e., 40°, 60°, 80°

Question 9. Find whether -150 is a term of the A.P. 17, 12, 7, 2, … ? (2011D)
Solution:
Given: 1^st term, a = 17
Common difference, d = 12 – 17 = -5
n^th term, a_n = – 150 (Let)
∴ a + (n – 1) d = – 150
17 + (n – 1)(-5) = – 150
(n – 1) (-5) = – 150 – 17 = – 167
(n − 1) = \(\frac{-167}{-5}\)
n = \(\frac{167}{5}\) + 1 = \(\frac{167+5}{5}=\frac{172}{5}\)
n = \(\frac{172}{5}\) …[Being not a natural number
∴ -150 is not a term of given A.P.

Also Check: Important Questions for Class 10 Maths Chapter 4 Quadratic Equations

Question 10. Which term of the progression 4, 9, 14, 19, … is 109? (2011D)
Solution:
Here, d = 9 -4 = 14 -9 = 19 – 14 = 5
∴ Difference between consecutive terms is constant.
Hence it is an A.P.
Given: First term, a = 4, d = 5, a_n = 109 (Let)
∴ a_n = a + (n – 1) d … [General term of A.P.
∴ 109 = 4 + (n – 1) 5
⇒ 109 – 4 = (n – 1) 5
⇒ 105 = 5(n − 1) ⇒ n – 1 = \(\frac{105}{5}\) = 21
⇒ n = 21 + 1 = 22 ∴ 109 is the 22^nd term

Question 11. Which term of the progression 20, 192, 183, 17 … is the first negative term? (2017OD)
Solution:
Given: A.P.: 20, \(\frac{77}{4}, \frac{37}{4}, \frac{71}{4}\)
Here a = 20, d = \(\frac{77-80}{4}=-\frac{3}{4}\)
For first negative term, a_n < 0
⇒ a + (n − 1)d < 0 ⇒ 20 + (n − 1)(-\(\frac{3}{4}\)) < 0
⇒ –\(\frac{3}{4}\)(n − 1) < -20 ⇒ 3(1 – 1) > 80
⇒ 3n – 3 > 80 ⇒ 3n > 83
n > \(\frac{83}{4}\) ⇒ n > 27.5
∴ Its negative term is 28th term.

Question 12. The 4^th term of an A.P. is zero. Prove that the 25th term of the A.P. is three times its 11^thterm. (2016OD)
Solution:
Let 1^st term = a, Common difference = d
a₄ = 0 a + 3d = 0 ⇒ a = -3d … (i)
To prove: a₂₅ = 3 × a₁₁
a + 24d = 3(a + 10d) …[From (i)
⇒ -3d + 24d = 3(-3d + 10d)
⇒ 21d = 21d
From above, a₂₅ = 3(a₁₁) (Hence proved)

Also Check: Surface Areas and Volumes Class 10 Extra Questions Maths Chapter 13

Question 13. The 7^th term of an A.P. is 20 and its 13^th term is 32. Find the A.P. (2012OD)
Solution:
Let a be the 1^th term and d be the common difference.

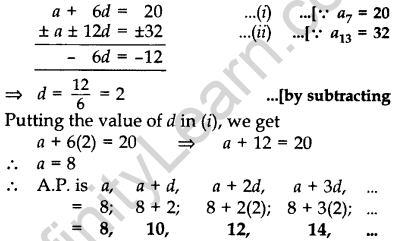
Question 14. Find 10th term from end of the A.P. 4,9, 14, …, 254. (2011OD)
Solution:
Common difference d = 9 – 4
= 14 – 9 = 5
Given: Last term, l = 254, n = 10
n^th term from the end = l – (n – 1) d
∴ 10^th term from the end = 254 – (10 – 1) × 5
= 254 – 45 = 209

Question 15. Find how many two-digit numbers are divisible by 6? (2011OD)
Solution:
12, 18, 24, …,96
Here, a = 12, d = 18 – 12 = 6, a_n = 96
a + (n – 1)d = a_n
∴ 12 + (n – 1)6 = 96
⇒ (n − 1)6 = 96 – 12 = 84
⇒ n – 1 = \(\frac{84}{6}\) = 14
⇒ n = 14 + 1 = 15
∴ There are 15 two-digit numbers divisible by 6.

Question 16. How many natural numbers are there between 200 and 500, which are divisible by 7? (2011OD)
Solution:
203, 210, 217, …, 497
Here a = 203, d = 210 – 203 = 7, a_n = 497
∴ a + (n – 1) d = a_n
203 + (n – 1) 7 = 497
(n – 1) 7 = 497 – 203 = 294
n – 1 = \(\frac{294}{7}\) = 42 ∴ n = 42 + 1 = 43
∴ There are 43 natural nos. between 200 and 500 which are divisible by 7.

Question 17. How many two-digit numbers are divisible by 3? (2012OD)
Solution:
Two-digit numbers divisible by 3 are:
12, 15, 18, …, 99
Here, a = 12, d = 15 – 12 = 3, a_n = 99
∴ a + (n – 1)d = a_n
12 + (n – 1) (3) = 99
(n – 1) (3) = 99 – 12 = 87
n – 1 = \(\frac{87}{3}\) = 29
∴ n = 29 + 1 = 30
∴ There are 30 such numbers.

Question 18. How many three-digit natural numbers are divisible by 7? (2013D)
Solution:
“3 digits nos.” are 100, 101, 102, …, 999
3 digits nos. “divisible by 7” are:
105, 112, 119, 126, …, 994
a = 105, d = 7, a_n = 994, n = ?
As a + (n – 1)d = 994 = a_n
∴ 105 + (n – 1)7 = 994
(n − 1)7 = 994 – 105
(n – 1) = \(\frac{889}{7}\) = 127
∴ n = 127 + 1 = 128

Question 19. Find the number of all three-digit natural numbers which are divisible by 9. (2013OD)
Solution:
To find: Number of terms of A.P., i.e., n.
A.P. = 108 + 117 + 126 + … + 999
1^st term, a = 108
Common difference, d = 117 – 108 = 9
a_n = 999
a + (n – 1)d = a_n
∴ 108 + (n – 1) 9 = 999
⇒ (n − 1) 9 = 999 – 108 = 891
⇒ (n − 1) = \(\frac{891}{9}\) = 99
∴ n = 99 + 1 = 100

Question 20. Find the number of natural numbers between 101 and 999 which are divisible by both 2 and 5. (2014OD)
Solution:
Numbers divisible by both 2 and 5 are 110, 120, 130, …, 990.
Here a = 110, d = 120 – 110 = 10, a_n = 990
As a + (n – 1)d = a_n = 990
110 + (n – 1)(10) = 990
(n – 1)(10) = 990 – 110 = 880
(n − 1) = \(\frac{294}{7}\) = 88
∴ n = 88 + 1 = 89

Question 21. Find the middle term of the A.P. 6, 13, 20, …, 216. (2015D)
Solution:
The given A.P. is 6, 13, 20, …, 216
Let n be the number of terms, d = 7, a = 6, a_n = 216
a_n = a + (n – 1)d
∴ 216 = 6 + (n – 1).7
216 – 6 = (n – 1)7
\(\frac{210}{7}\) = n – 1 ⇒ 30 + 1 = n
⇒ n = 31
Middle term = \(\left(\frac{n+1}{2}\right)^{t h}\) term
= \(\left(\frac{31+1}{2}\right)=\left(\frac{32}{2}\right)\) = 16^th term of the A.P.
∴ a₁₆ = a + 15d = 6 + 15 × 7 = 111

Question 22. Find the middle term of the A.P. 213, 205, 197, … 37. (2015D)
Solution:
A.P. : 213, 205, 197, …………. 37.
Let a and d be the first term and common difference of A.P. respectively,
Here a = 213, d = -8, a_n = 37, where n is the number of terms.
a_n = a + (n – 1)d
∴ 37 = 213 + (n – 1) (-8)
\(\frac{-176}{-8}\) = n – 1 ⇒ n = 23
∴ Middle term = \(\left(\frac{n+1}{2}\right)^{\text { th }}=\left(\frac{23+1}{2}\right)\)
= 12^th term
∴ a₁₂ = a + 11(d) = 213 + 11(-8) = 125

Question 23. How many terms of the A.P. 27, 24, 21, … should be taken so that their sum is zero? (2016D)
Solution:
Here, 1^st term, a = 27
Common difference, d = 24 – 27 = -3
Given: S_n = 0
⇒ \(\frac{n}{2}\)[2a + (n − 1)d] = 0
⇒ \(\frac{n}{2}\)[2(27) + (n − 1)(-3)] = 0
⇒ n(54 – 3n + 3) = 0
⇒ n(57 – 3n) = 0
⇒ n = 0 or (57 – 3n) = 0
⇒ -3n = -57
⇒ n = 19
Since n, i.e., number of terms cannot be zero.
∴ Number of terms = 19

Question 24. How many terms of the A.P. 65, 60, 55, … be taken so that their sum is zero? (2016D)
Solution:
1^st term, a = 65
Common difference, d = 60 – 65 = -5
S_n = 0 …[Given
⇒ \(\frac{n}{2}\)[2a + (n − 1)d] = 0
⇒ \(\frac{n}{2}\)[2(65) + (n − 1)(-5)] = 0
⇒ n(130 – 5n + 5) = 0
⇒ n(135 – 5n) = 0
⇒ n = 0 or 135 – 5n = 0
-5n = -135
⇒ n = 27
Since n, i.e., number of terms can not be zero.
∴ Number of terms = 27

Question 25. Find the sum of the first 25 terms of an A.P. whose n^th term is given by t_n = 2 – 3n. (2012D)
Solution:
Given: t_n = 2 – 3n
When n = 1, t₁ = 2 – 3(1) = -1 ..(i)
When n = 25, t₂₅ = 2 – 3(25) = -73 …(ii)
As S_n = \(\frac{n}{2}\)[t₁ + t_n], n = 25
∴ S₂₅ = \(\frac{25}{2}\)[-1 + (-73)] .. [From (1) and (ii)
= \(\frac{25 \times(-74)}{2}\) = 25 × (-37) = -925

Question 26. The first and the last terms of an AP are 5 and 45 respectively. If the sum of all its terms is 400, find its common difference. (2014D)
Solution:
Here, a_n = 45, S_n = 400, a = 5, n = ?, d = ?

Question 27. The first and the last terms of an AP are 8 and 65 respectively. If the sum of all its terms is 730, find its common difference. (2014D)
Solution:
Here a, = a = 8; a_n = 65
Given: S_n = 730
⇒ \(\frac{n}{2}\)(8 + 65) = 730 …..[S_n = \(\frac{n}{2}\)(a₁ + a_n)
\(\frac{n}{2}\)(73) = 730
n = 730 × \(\frac{2}{73}\) = 20
Now, a_n = a + (n − 1)d = 65
8 +(20 – 1)d = 65 ⇒ 19d = 65 – 8 = 57
∴ d = 3

Question 28. In an AP, if S₅ + S₇ = 167 and S₁₀ = 235, then find the AP, where s, denotes the sum of its first n terms. (2015OD)
Solution:
Given: S₅ + S₇ = 167
⇒ \(\frac{5}{2}\)[2a + (5 – 1)d] + \(\frac{7}{2}\) [2a + (7 – 1)d] = 167 … [S<sub<n = \(\frac{n}{2}\) (2a + (n – 1)d)
⇒ \(\frac{5}{2}\)[2a + 4d] + \(\frac{7}{2}\)[2a + 6d] = 167
⇒ 5(a + 2d) + 7(a + 3d) = 167
⇒ 5a + 10d + 7a + 210 = 167
⇒ 12a + 31d = 167
Now, S₁₀ = \(\frac{10}{2}\) (2a + (10 – 1)d) = 235
⇒ 5[2a + 9d] = 235
⇒ 10a + 45d = 235
Solving (i) and (ii), we get a = 1 and d = 5
a₁ = 1
a₂ = a + d ⇒ 1 + 5 = 6
a₃ = a + 2d ⇒ 1 + 10 = 11
Hence A.P. is 1, 6, 11…

Question 29. Find the sum of all three digit natural numbers, which are multiples of 11. (2012D)
Solution:
To find: 110 + 121 + 132 + … + 990
Here a = 110, d = 121- 110 = 11, a_n = 990
∴ a + (n – 1)d = 990
110 + (n – 1).11 = 990
(n – 1). 11 = 990 – 110 = 880
(n – 1) = 880 = 80
n = 80 + 1 = 81
As S_n = \(\frac{n}{2}\) (a₁ + a_n)
∴ S₈₁ = \(\frac{81}{2}\) (110 + 990)
= \(\frac{81}{2}\) (1100) = 81 × 550 = 44,550

Arithmetic Progressions Class 10 Important Questions Short Answer – II (3 Marks)

Question 30. Which term of the A.P. 3, 14, 25, 36, … will be 99 more than its 25th term? (2011OD)
Solution:
Let the required term be n^th term, i.e., a_n
Here, d = 14 – 3 = 11, a = 3
According to the Question, a_n = 99 + a₂₅
∴ a + (n – 1) d = 99 + a + 24d
⇒ (n – 1) (11) = 99 + 24 (11)
(n – 1) (11) = 11 (9 + 24)
n – 1 = 33
n = 33 + 1 = 34
∴ 34^th term is 99 more than its 25th term.

Question 31. Determine the A.P. whose fourth term is 18 and the difference of the ninth term from the fifteenth term is 30. (2011D)
Solution:

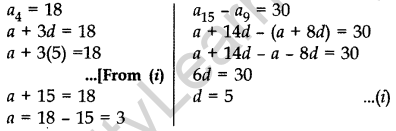
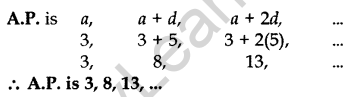
Question 32. The 19th term of an AP is equal to three times its 6^th term. If its 9^th term is 19, find the A.P. (2013OD)
Solution:
Given: a₁₉ = 3(a₆)
⇒ a + 18d = 3(a + 5d)
a + 18d = 3a + 15d
18d – 15d = 3a – a

Question 33. The 9th term of an A.P. is equal to 6 times its second term. If its 5^th term is 22, find the A.P. (2013OD)
Solution:
9^th term = 6 (2^nd term)
∴ a +8d = 6 (a + d) …[As a_n = a + (n – 1)d
a + 8d = 6a + 6d
8d – 6d = 6a – a
2d = 5a
⇒ d = \(\frac{5 a}{2}\) …(i)
Now, a₅ = 22
a + 4d = 22

Question 34. The sum of the 5th and the 9th terms of an AP is 30. If its 25^th term is three times its 8^th term, find the AP. (2014OD)
Solution:
a₅ + a₉ = 30 … [Given
a + 4d + a + 8d = 30 …[∵ a_n = a + (n – 1)d
2a + 12d = 30 ⇒ a + 6d = 15 …[Dividing by 2
a = 15 – 6d …(i)
Now, a₅₂ = 3(a₈)
a + 24d = 3(a + 7d)
15 – 6d + 240 = 3(15 – 6d + 7d) …[From (i)
15 + 18d = 3(15 + d)
15 + 18d = 45 + 3d
18d – 3d = 45 – 15
15d = 30 ∴ d = \(\frac{30}{15}\) = 2
From (i), a = 15 – 6(2) = 15 – 12 = 3

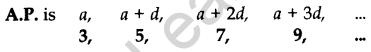
Question 35. If the seventh term of an AP is \(\frac{1}{9}\) and its ninth term is \(\frac{1}{7}\), find its 63^rd term. (2014D)
Solution:

Question 36. Find the value of the middle term of the following A.P.: -6, -2, 2, …, 58. (2011D)
Solution:
Here a = -6, d = -2 -(-6) = 4, a_n = 58
As we know, a + (n – 1) d = 58
∴ -6 + (n – 1) 4 = 58
⇒ (n – 1) 4 = 58 + 6 = 64
⇒ (n – 1) = \(\frac{64}{4}\) = 16
⇒ n = 16 + 1 = 17 (odd)
Middle term = \(\left(\frac{n+1}{2}\right)^{t h}\) term
\(\left(\frac{17+1}{2}\right)^{t h}\) term = 9^th term
∴ a₉ = a + 8d = -6 + 8 (4) = -6 + 32 = 26
∴ Middle term = 26

Question 37. Find the number of terms of the AP 18, 151/2, 13,…, -491/2 and find the sum of all its terms.
Solution:
Here 1^st term, a = 18

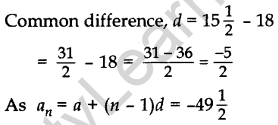
Question 38. The 14^th term of an AP is twice its g^th term. If its 6^th term is -8, then find the sum of its first 20 terms. (2015OD)
Solution:
Let a = First term, d = Common difference
a₁₄ = 2.a₈ … [Given
⇒ a + 13d = 2 (a + 7d) ..[∵ a, = a + (n – 1)d
⇒ a + 13d = 2a + 14d
⇒ 1a – 2a = 14d – 13d
⇒ -1a = d ⇒ a = -d … (i)
a₆ = -8 …[Given
⇒ -8 = a + 5d
⇒ -d + 5d = -8 …[From (i)
⇒ 4d = -8 ⇒ d = -2
Value of d put in equation (i), we get
a = -d ⇒ a=-(-2)
Now, a = 2, d = -2
Now, Sum of first 20 terms,
S₂₀ = \(\frac{20}{2}\)[2 × 2 + (20 – 1)(-2)] …[S_n = \(\frac{n}{2}\) (2a + (n – 1)d)
S₂₀ = 10[4 + 19(-2)] S₂₀ = 10[4 – 38] = -340

Question 39. The 13th term of an AP is four times its 3rd term. If its fifth term is 16, then find the sum of its first ten terms. (2015OD)
Solution:
a₁₃ = 4a₃ … [Given
⇒ a + 12d = 4(a + 2d) …[∵ a_n = a + (n – 1)d
⇒ a + 12d – 4a – 8d = 0
⇒ 4d = 3a ⇒ d = \(\frac{3 a}{4}\) …(i)
a₅ = 16 … [Given
⇒ a + 4d = 16
⇒ a +4(\(\frac{3 a}{4}\)) = 16 … [From (i)
⇒ a + 3a = 16
⇒ 4a = 16 ⇒ a = \(\frac{16}{4}\) = 4 ..(ii)
Putting a = 4 in (i), we get a = 3
⇒ d = \(\frac{3 \times 4}{4}\) = 3 … [From (ii)
∴ S_n = \(\frac{n}{2}\) [2a + (n – 1)d] S₁₀ = \(\frac{10}{2}\) [2(4) + (10 – 1)(3)] …[n = 10 (Given)
S₁₀ = 5 (8 + 27) ⇒ 5(35) = 175

Question 40. If the sum of first 7 terms of an A.P is 49 and that of its first 17 terms is 289, find the sum of first n terms of the A.P. (2016D)
Solution:
Let 1^st term = a, Common difference = d
Given: S₇ = 49, S₁₇ = 289

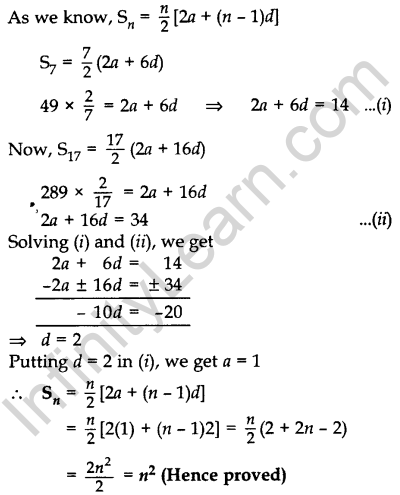
Question 41. The first term of an A.P. is 5, the last term is 45 and the sum of all its terms is 400. Find the number of terms and the common difference of the A.P. (2017OD)
Solution:
First term, a = 5, Last term, a_n = 45
Let the number of terms = n
S_n = 400
\(\frac{n}{2}\) (a + a_n) = 400
\(\frac{n}{2}\)(5 + 45) = 400
\(\frac{n}{2}\) (50) = 400
n = \(\frac{400}{25}\) = 16 = Number of terms
Now, a_n = 45
a + (n – 1)d = a_n
5+ (16 – 1)d = 45
15d = 45 – 5 ∴ d = \(\frac{40}{15}=\frac{8}{3}\)

Question 42. The n^th term of an A.P. is given by (-4n + 15). Find the sum of first 20 terms of this A.P. (2013D)
Solution:
We have, a_n = -4n + 15
Put n = 1, a₁ = -4(1) + 15 = 11
Put n=2, a₂ = -4(2) + 15 = 7
∴ d = a₂ – a₁ = 7 – 11 = -4
As S_n = \(\frac{n}{2}\) (2a + (n – 1)d] ∴ S₂₀ = \(\frac{20}{2}\) [2(11) + (20 – 1)(-4))… [n = 20 (Given)
= 10 (22 – 76)
= 10 (-54) = -540

Question 43. The sum of first n terms of an AP is 3n² + 4n. Find the 25^th term of this AP. (2013D)
Solution:
We have, S_n = 3n² + 4n
Put n = 25,
S₂₅ = 3(25)² + 4(25)
= 3(625) + 100
= 1875 + 100 = 1975
Put n = 24,
S₂₄ = 3(24)² + 4(24)
= 3(576) + 96
= 1728 + 96 = 1824
∴ 25^th term = S₂₅ – S₂₄
= 1975 – 1824 = 151

Question 44. The sum of the first seven terms of an AP is 182. If its 4^th and the 17^th terms are in the ratio 1 : 5, find the AP. (2014OD)
Solution:
S₇ = 182 …[Given

∴ a = 2, d = 8
∴AP is 2, 10, 18, 26, 34, …

Question 45. If S_n, denotes the sum of first n terms of an A.P., prove that S₁₂ = 3(S₈ – S₄). (2015D)
Solution:
Let a be the first term and d be the common difference of A.P.
S_n = \(\frac{n}{2}\) (2a + (n − 1)d)
∴ S₁₂ = \(\frac{12}{2}\) (2a + (12 – 1)d)
S₁₂ = 6 [2a + 11d] = 124 + 66d …(i)
∴ S₈ = \(\frac{8n}{2}\) (2a + (8 – 1)d)
S₈ = 4[2a + 7d] = 8a + 28d … (ii)
∴ S₄ = \(\frac{4}{2}\) (2a + (4 – 1)d)
S₄ = 2[2a + 3d) = 4a + 6d …(iii)
Now, S₁₂ = 3(S₈ – S₄)
12a + 660 = 3(8a + 28d – 4a – 6d) … [From (i), (ii) & (iii)
12a + 660 = 3(4a + 22d)
12a + 660 = 12a + 66d …Hence proved

Question 46. If the sum of the first n terms of an A.P. is \(\frac{1}{2}\) (3n² + 7n), then find its n^th term. Hence write its 20^th (2015D)
Solution:
S_n = \(\frac{1}{2}\) (3n² + 7n) …[Given
Put n = 1
S₁ = \(\frac{1}{2}\)[3(1)₂ + 7(1)] = \(\frac{1}{2}\) [3 + 7) = \(\frac{1}{2}\) (10) = 5
Put n = 2
S₂ = \(\frac{1}{2}\) [3(2)² + 7(2)] = \(\frac{1}{2}\)[3(4) + 7(2)] = S₂ = \(\frac{1}{2}\)(12 + 14) = \(\frac{1}{2}\) (26) = 13
Now we know,
S₁ = 27 and a₂ = S₂ – S₁
∴ a₁ = 5 = 13 – 5 = 8
Now we have,
a₁ = 5, a₂ = 8, d = a₂ – a₁ = 8 – 5 = 3
a_n = a + (n – 1)d = 5 + (n – 1)3
= 5 + 3n – 3 = 3n + 2 (n^th term)
∴ 20^th term, a₂₀ = (3 × 20) + 2 = 62

Question 47. If S_n denotes the sum of first n terms of an A.P., prove that S₃₀ = 3[S₂₀ – S₁₀]. (2015D)
Solution:
Let a be the first term and d be the common difference of the A.P.
S_n = \(\frac{n}{2}\)[2a + (n − 1)d] S₃₀ = \(\frac{30}{2}\) [2a + (30 – 1)d] = 15[2a + 29d] = 30a + 435d …(i)
S₂₀ = \(\frac{20}{2}\) [2a + (20 – 1)d] = 10[2a + 19d] = 20a + 190d …(ii)
S₁₀ = \(\frac{10}{2}\)[2a + (10 – 1)d] = 5[2a + 9d] = 10a + 45d …(iii)
To prove, 3(S₂₀ – S₁₀) = S₃₀
= 3(20a + 190d – 10a – 45d) …[From (i), (ii) & (iii)
= 3(10a + 145d)
= 30a + 435d = S₃₀ …Hence Proved

Question 48. If the ratio of the sum of first n terms of two A.Ps is (7n + 1): (4n + 27), find the ratio of their mth terms. (2016OD)
Solution:
Let A be first term and D be the common difference of 1^st A.P.
Let a be the first term and d be the common difference of 2^nd A.P.

∴ Required ratio = (14m – 6) : (8m + 23)

Question 49. The digits of a positive number of three digits are in A.P. and their sum is 15. The number obtained by reversing the digits is 594 less than the original number. Find the number. (2016OD)
Solution:
Let hundred’s place digit = (a – d)
Let ten’s place digit = a
Let unit’s place digit = a + d
According to the Question,
a – d + a + a + d = 15
⇒ 3a = 15 ⇒ a = 5
Original number
= 100(a – d) + 10(a) + 1(a + d)
= 100a – 100d + 10a + a + d
= 111a – 99d
Reversed number
= 1(a – d) + 10a + 100(a + d)
= a – d + 10a + 100a + 100d
= 111a + 99d
Now, Original no. – Reversed no. = 594
111a – 99d – (111a + 99d) = 594
-198d = 594 ⇒ d = \(\frac{594}{-198}\) = -3
∴ The Original no. = 111a – 99d
= 111(5) – 99(-3)
= 555 + 297 = 852

Question 50. The sums of first n terms of three arithmetic progressions are S₁ S₂ and S₃ respectively. The first term of each A.P. is 1 and their common differences are 1, 2 and 3 respectively. Prove that S₁ + S₃ = 2S₂. (2016OD)
Solution:

Question 51. Find the sum of all three digit natural numbers, which are multiples of 9. (2012D)
Solution:
To find: 108 + 117 + 126 + … + 999
1^st term, a = 108
Common difference, d = 117 – 108 = 9
∴ a + (n – 1)d = a_n = 999
108 + (n – 1). 9 = 999
(n – 1)9 = 999 – 108 = 891
(n – 1) = \(\frac{891}{9}\) = 99
n = 99 + 1 = 100
As S_n= \(\frac{n}{2}\)(a₁ + a_n)
∴ S₁₀₀ = \(\[\frac{100}{2}\)\] (108 + 999)
= 50(1107) = 55350

Question 52. Find the sum of all multiples of 7 lying between 500 and 900. (2012OD)
Solution:
To find: 504 + 511 + 518 + … + 896
a = 504, d = 511- 504 = 7, a_n = 896
a + (n – 1)d = a_n
∴ 504 + (n – 1)7 = 896
(n – 1)7 = 896 – 504 = 392

Arithmetic Progressions Class 10 Important Questions Long Answer (4 Marks)

Question 53. If p^th, q^th and r^th terms of an A.P. are a, b, c respectively, then show that (a – b)r + (b – c)p+ (c – a)q = 0. (2011D)
Solution:
Let A be the first term and D be the common difference of the given A.P.
p^th term = A + (p – 1)D = a …(i)
q^th term = A + (q – 1)D = b …(ii)
r^th term = A + (r – 1)D = c … (iii)
L.H.S. = (a – b)r + (b – c)p + (c – a)q
= [A + (p – 1)D – (A + (q – 1)D)]r + [A + (q – 1)D – (A + (r – 1)D)]p + [A + (r – 1)D – (A + (p – 1)D)]q
= [(p – 1 – q + 1)D]r + [(q – 1 – r + 1)D]p + [(r – 1 – p + 1)D]q
= D[(p – q)r + (q – r)p + (r – p)q] = D[pr – qr + qp – rp + rq – pq] = D[0] = 0 = R.H.S.

Question 54. The 17^th term of an AP is 5 more than twice its 8^th term. If the 11^th term of the AP is 43, then find its n^th term. (2012D)
Solution:

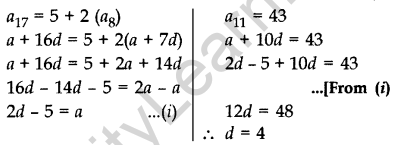
From (i),
a = 2(4) – 5 = 8 – 5 = 3
As a_n = a + (n – 1) d
∴ a_n = 3 + (n – 1) 4 = 3 + 4n – 4
a_n = (4n – 1)

Question 55. The 15^th term of an AP is 3 more than twice its 7^th term. If the 10^th term of the AP is 41, then find its n^th term. (2012D)
Solution:

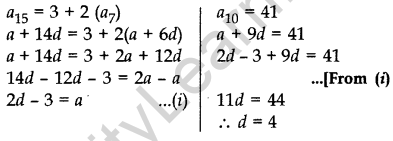
From (i),
a = 2(4) – 3
= 8 – 3 = 5
n^th term = a + (n – 1) d
∴ n^th term = 5 + (n – 1) 4
= 5 + 4n – 4 = (4n + 1)

Question 56. The 16^th term of an AP is 1 more than twice its 8^th term. If the 12^th term of the AP is 47, then find its n^th term. (2012D)
Solution:

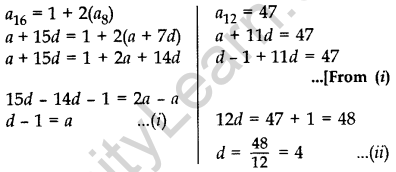
From (i) and (ii), a = 4 – 1 = 3
As n^th term = a + (n – 1) d
∴ n^th term = 3 + (n – 1) 4
= 3 + 4n -4 = 4n -1

Question 57. A sum of ₹1,600 is to be used to give ten cash prizes to students of a school for their overall academic performance. If each prize is ₹20 less than its preceding prize, find the value of each of the prizes. (2012OD)
Solution:
Here S₁₀ = 1600, d = -20, n = 10
S_n = \(\frac{n}{2}\) (2a + (n – 1)d] ∴ \(\frac{10}{2}\)[2a + (10 – 1)(-20)] = 1600
2a – 180 = 320
2a = 320 + 180 = 500
a = 250
∴ 1^st prize = a = ₹250
2^nd prize = a₂ = a + d = 250 + (-20) = ₹230
3^rd prize = a₃ = a₂ + d = 230 – 20 = ₹210
4^th prize = a₄ = a₃ + d = 210 – 20 = ₹190
5^th prize = a₅ = a₄ + d = 190 – 20 = ₹170
6^th prize = a₆ = a₅ + d = 170 – 20 = ₹150
7^th prize = a₇ = a₆ + d = 150 – 20 = ₹130
8^th prize = a₈ = a₇ + d = 130 – 20 = ₹110
9^th prize = a₉ = a₈ + d = 110 – 20 = ₹590
10^th prize = a₁₀ = a₉ + d = 90 – 20 = ₹70
= ₹ 1,600

Question 58. Find the 60th term of the AP 8, 10, 12, …, if it has a total of 60 terms and hence find the sum of its last 10 terms. (2015OD)
Solution:
a = 8, d = a₂ – a₁ = 10 – 8 = 2, n = 60
a₆₀ = a + 59d = 8 + 59(2) = 126
∴ Sum of its last 10 terms = S₆₀ – S₅₀
= \(\frac{n}{2}\)(a + a_n) – \(\frac{n}{2}\)(2a + (n – 1)d)
= \(\frac{60}{2}\) (8 + a₆₀) – \(\frac{50}{2}\) (2 × 8 + (50 – 1)2)
= 30 (8 + 126) – 25 (16 + 98)
= 4020 – 25 × 114
= 4020 – 2850 = 1170

Question 59.
An Arithmetic Progression 5, 12, 19, … has 50 terms. Find its last term. Hence find the sum of its last 15 terms. (2015OD)
Solution:
Let a and d be the first term and common difference of A.P. respectively,
a = 5, d = 12 – 5 = 7, n = 50
∴ a_n = a + (n – 1)d
a₅₀ = 5 + 49(7) = 5 + 343 = 348
∴ Sum of its last 15 terms = S₅₀ – S₃₅
= \(\frac{n}{2}\)(a + a_n) – \(\frac{n}{2}\) (2a + (n − 1)d)
= \(\frac{50}{2}\) (5 + 348) – \(\frac{35}{2}\) [2(5) + (35 – 1)7] = 25(353) – \(\frac{35}{2}\) (10 + 238)
= 8825 – 35 × 124
= 8825 – 4340 = 4485

Question 60.
If the sum of first 4 terms of an A.P. is 40 and that of first 14 terms is 280, find the sum of its first n terms. (2011D)
Solution:
S_n = \(\frac{n}{2}\)[2a + (n − 1) d] …(i)

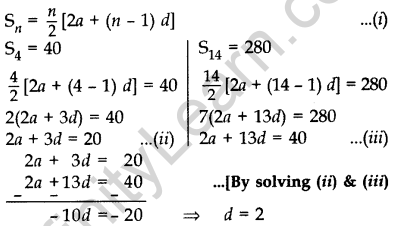
Putting the value of d = 2 in (ii), we get a = 7
∴ S_n = \(\frac{n}{2}\)[2(7) + (n – 1). 2] = \(\frac{n}{2}\).2 [7 + n – 1] = n (n + 6) or n² + 6n

Question 61.
The first and the last terms of an A.P. are 8 and 350 respectively. If its common difference is 9, how many terms are there and what is their sum? (2011D)
Solution:
Here a = 8, a_n = 350, d = 9
As we know, a + (n − 1) d = a₂
∴ 8 + (n – 1) 9 = 350
(n − 1) 9 = 350 – 8 = 342
n – 1 = \(\frac{342}{9}\) = 38
n = 38 + 1 = 39
∴ There are 39 terms.
∴ S_n = \(\frac{n}{2}\)(a + an)
∴ S₃₉ = \(\frac{39}{2}\) (8 + 350) = \(\frac{39}{2}\) × 358
= 39 × 179 = 6981

Question 62.
Sum of the first 20 terms of an AP is -240, and its first term is 7. Find its 24^th term. (2012D)
Solution:
Given: a = 7, S₂₀ = -240
Here, S_n = \(\frac{n}{2}\)[2a + (n – 1)d] ∴ S₂₀ = \(\frac{20}{2}\)[2(7) + (20 – 1)d] -240 = 10(14 + 19d)
–\(\frac{240}{10}\) = 14 + 19d = -24
19d = -24 – 14 = -38
⇒ d = \(\frac{-38}{19}\) = -2 …(i)
Again, a_n = a + (n – 1)d
∴ a₂₄ = 7 + (24 – 1) (-2) … [From (i)
= 7 – 46 = -39

Question 63.
Find the common difference of an A.P. whose first term is 5 and the sum of its first four terms is half the sum of the next four terms. (2012OD)
Solution:
Here a = 5 … (i)
Here, a₁ + a₂ + a₃ + a₄ = \(\frac{1}{2}\) (a₅ + a₆ + a₇ + a₈)
∴ a + (a + d) + (a + 2d) + (a + 3d)
= \(\frac{1}{2}\) [(a + 4d) + (a + 5d) + (a + 6d) + (a + 780] …[a_n = a(n – 1)d
∴ 4a + 6d = \(\frac{1}{2}\) (4a + 22d)
8a + 12d = 4a + 22d
8a – 4a = 22d – 12d
4a = 100 ⇒ 4(5) = 10d
d = \(\frac{4(5)}{10}=\frac{20}{10}\) = 2 …[From (1)
∴ Common difference, d = 2

Question 64.
If the sum of the first 7 terms of an A.P. is 119 and that of the first 17 terms is 714, find the sum of its first n terms. (2012OD)
Solution:
As S_n = \(\frac{n}{2}\)[2a + (n − 1)d]
S₂ = 119
From (i) and (ii), a = 17 – 3(5) = 17 – 15 = 2
∴S_n = \(\frac{1}{2}\)[2(2) + (n – 1)5] = \(\frac{n}{2}\)[4 + 5n – 5] = \(\frac{n}{2}\) (5n – 1)

Question 65.
The 24^th term of an AP is twice its 10th term. Show that its 72^nd term is 4 times its 15th term. (2013D)
Solution:
a₂₄ = 2 (10) … [Given
a + 23d = 2 (a +9d) [∵ a_n = a + (n – 1)d)
23d = 2a + 18d – a
23d – 18d = a ⇒ a = 5d …(i)
To prove: a₇₂ = 4 (a₁₅)

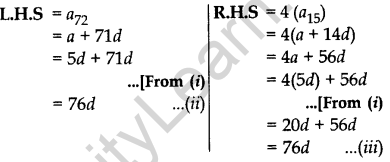
From (ii) and (iii), L.H.S = R.H.S …Hence Proved

Question 66.
Find the number of terms of the A.P. -12, -9, – 6, …, 21. If 1 is added to each term of this A.P., then find the sum of all terms of the A.P. thus obtained. (2013D)
Solution:
Here a = -12, d=-9 + 12 = 3
Here, a_n = a + (n – 1)d = 21
∴ -12 + (n – 1).3 = 21
(n – 1).3 = 21 + 12 = 33
∴ n – 1 = 11
Total number of terms,
n = 11 + 1 = 12
New A.P. is

Here 1st term, a = -11
Common difference, d = -8 + 11 = 3;
Last term, a_n = 22; Number of terms, n= 12

Question 67.
In an AP of 50 terms, the sum of first 10 terms is 210 and the sum of its last 15 terms is 2565. Find the AP. (2014D)
Solution:
Here, n = 50,
Here, S₁₀ = 210
= \(\frac{10}{2}\) (2a + 9d) = 210 ….[S_n = \(\frac{1}{2}\) [2a+(n – 1)2] 5(2a + 9d) = 210
2a + 9d = \(\frac{210}{5}\) = 42
⇒ 2a = 42 – 9d ⇒ a = \(\frac{42-9 d}{2}\) …(i)
Now, 50 = (1 + 2 + 3 + …) + (36 + 37 + … + 50) Sum = 2565
Sum of its last 15 terms = 2565 …[Given
S₅₀ – S₃₅ = 2565
\(\frac{50}{2}\)(2a + 49d) – \(\frac{35}{2}\) (2a + 34d) = 2565
100a + 2450d – 70a – 1190d = 2565 × 2
30a + 1260d = 5130
3a + 1260 = 513 …[Dividing both sides by 10

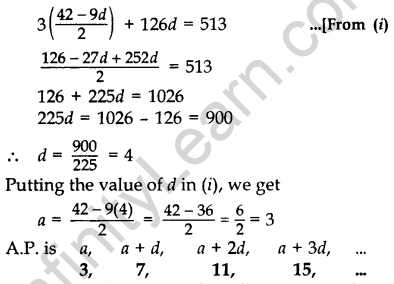
Question 68.
If the ratio of the sum of the first n terms of two A.Ps is (7n + 1): (4n + 27), then find the ratio of their 9^th terms. (2017OD)
Solution:

Question 69.
In a school, students decided to plant trees in and around the school to reduce air pollution. It was decided that the number of trees, that each section of each class will plant, will be double of the class in which they are studying. If there are 1 to 12 classes in the school and each class has two Sections, find how many trees were planted by the students. (2014OD)
Solution:
Classes: 1 + I + II + … + XII
Sections: 2(I) + 2(II) + 2(III) + … + 2(XII)
Total no. of trees
= 2 + 4 + 6 … + 24
= (2 × 2) + (2 × 4) + (2 × 6) + … + (2 × 24)
= 4 + 8 + 12 + … + 48
:: S₁₂ = \(\frac{12}{2}\)(4 + 48) = 6(52) = 312 trees

Question 70.
Ramkali required ₹500 after 12 weeks to send her daughter to school. She saved ₹100 in the first week and increased her weekly saving by ₹20 every week. Find whether she will be able to send her daughter to school after 12 weeks. (2015D)
Solution:
Money required by Ramkali for admission of her daughter = ₹2500
A.P. formed by saving
100, 120, 140, … upto 12 terms ….(i)
Let, a, d and n be the first term, common difference and number of terms respectively. Here, a = 100, d = 20, n = 12
S_n = \(\frac{n}{2}\) (2a + (n − 1)d)
⇒ S₁₂ = \(\frac{12}{2}\) (2(100) + (12 – 1)20)
S₁₂ = \(\frac{12}{2}\) [2(100) + 11(20)] = 6[420] = ₹2520

Question 71.
The sum of first n terms of an A.P. is 5n² + 3n. If its m^th term is 168, find the value of m. Also find the 20^th term of this A.P. (2013D)
Solution:

Question 72.
The sum of first m terms of an AP is 4m² – m. If its n^th term is 107, find the value of n. Also find the 21^st term of this A.P. (2013D)
Solution:
We have, S_m = 4m² – m
Put m = 1,
S₁ = 4(1)² – (1)
= 4 – 1 = 3
Put m = 2,
S₂ = 4(2)² – 2
= 16 – 2 = 14
∴ a₁ = S₁ = 3 = a
a₂ = S₂ – S₁ = 14 – 3 = 11
d = a₂ – a₁
d = 11 – 3 = 8
a_n = a + (n – 1)d = 107 …[Given
∴ 3+ (n – 1)8 = 107
(n – 1)8 = 107 – 3 = 104
(n – 1) = \(\frac{104}{8}\) = 13
n = 13 + 1 = 14
∴ a₂₁ = a + 20d
= 3 + (20)8
= 3 + 160 = 163

Question 73.
The sum of first g terms of an A.P. is 63q – 3q². If its p^th term is -60, find the value of p. Also find the 11^th term of this A.P. (2013D)
Solution:
We have, S_q = 63q – 3q²
Put q = 1,
S₇ = 63(1) – 3(1)²
= 63 – 3 = 60
Put q = 2,
S2 = 63(2) – 3(2)²
= 126 – 12 = 114
∴ a = a₁ = S₁ = 60
a₂ = S₂ – S7₁ = 114 – 60 = 54
d = a₂ – a₁ = 54 – 60 = -6
p^th term = -60
a + (p – 1)d = -60
60 + (p – 1)(-6) = -60
(p – 1)(-6) = -60 – 60 = -120
(p – 1) = \(\frac{-120}{-6}\) = 20
p= 20 + 1 = 21
∴ a₁₁ = a + 10d
= 60 + 10(-6)
= 60 – 60 = 0

Question 74.
Find the sum of the first 30 positive integers divisible by 6. (2011D)
Solution:
To find: 6 + 12 + 18 + … (30 terms)
Here a = 6, d = 12 – 6 = 6, n = 30
S_n = [2a + (n − 1) d] ∴ S₃₀ = \(\frac{30}{2}\)[2(6) + (30 – 1) 6] = 15 [12 + 29(6)] = 15 (12 + 174)
= 15 (186) = 2790

Question 75.
How many multiples of 4 lie between 10 and 250? Also find their sum. (2011D)
Solution:
Multiples of 4 between 10 and 250 are:
12, 16, 20, ……… 248
Here, a = 12, d = 4, a_n = 248
As we know, a + (n – 1) d = a_n
∴12 + (n – 1) 4 = 248
⇒ (n – 1) 4 = 248 – 12 = 236
n – 1 = \(\frac{236}{4}\) = 59
⇒ n = 59 + 1 = 60
∴ There are 60 terms.
Now, S_n = \(\frac{n}{2}\) (a + a_n)
∴ S₆₀ = \(\[\frac{60}{2}\)\](12 + 248)
= 30 (260) = 7800

Question 76.
Find the sum of all multiples of 8 lying between 201 and 950. (2012OD)
Solution:
To find: 208 + 216 +224 + … + 944
Here, a = 208, d = 216 – 208 = 8, a_n = 944
a + (n – 1)d = a_n
∴ 208 + (n – 1)8 = 944
(n – 1)8 = 944 – 208 = 736
n – 1 = \(\frac{736}{8}\) = 92
8 n = 92 + 1 = 93
Now, S_n = \(\frac{n}{2}\)(a₁ + a_n)
:: S₉₃ = \(\frac{93}{2}\) (208 + 944)
= \(\frac{93}{2}\) × 1152 = 93 × 576 = 53568

Question 77.
Find the sum of all multiples of 9 lying between 400 and 800. (2012OD)
Solution:
To find: 405 + 414 + 423 + … +792
Here a = 405, d = 414 – 405 = 9, a_n = 792
a + (n – 1)d = a_n
∴ 405 + (n – 1)9 = 792
(n – 1)9 = 792 – 405 = 387
n – 1 = \(\frac{387}{9}\) = 43
∴ n = 43 + 1 = 44
As S_n = \(\frac{n}{2}\)(a₁ + a_n)
∴ S₄₄ = \(\frac{44}{2}\) (405 + 792)
= 22 × 1197 = 26334

Question 78.
A thief runs with a uniform speed of 100 m/minute. After one minute a policeman runs after the thief to catch him. He goes with a speed of 100 m/minute in the first minute and increases his speed by 10 m/minute every succeeding minute. After how many minutes the policeman will catch the thief. (2016D)
Solution:
Let total time ben minutes. Total distance covered by thief in n minutes
= Speed × Time
= 100 × n = 100 n metres
Total distance covered by policeman

⇒ (n – 1) (200 + 10n – 20) = 200n
⇒ (n – 1) [10n + 180) = 200n
⇒ 10n² + 180n – 10n – 180 – 200n = 0
⇒ 10n² – 30n – 180 = 0
⇒ n² – 3n – 18 = 0 … [Dividing both sides by 10
⇒ n² – 6n + 3n – 18 = 0
⇒ n(n – 6) + 3(n – 6) = 0
⇒ (n + 3) (n – 6) = 0
⇒ n + 3 = 0 or n – 6 = 0
⇒ n = -3 or n = 6
But n (time) can not be negative.
∴ Time taken by policeman to catch the thief
= n – 1 = 6 – 1 = 5 minutes

Question 79.
A thief, after committing a theft, runs at a uniform speed of 50 m/minute. After 2 minutes, a policeman runs to catch him. He goes 60 m in first minute and increases his speed by 5 m/ minute every succeeding minute. After how many minutes, the policeman will catch the thief? (2016D)
Solution:
Let total time be n minutes.
Total distance covered by thief in n minutes
= Speed × Time
= (50 × n) metres = 50 n metres
Total distance covered by policeman

⇒ (n – 2) (120 + 5n – 15) = 100n
⇒ (n – 2) [5n + 105) = 100n
⇒ 5n² + 105n – 10n – 210 – 100n = 0
⇒ 5n² – 5n – 210 = 0
⇒ n² – n – 42 = 0 …[Dividing both sides by 5
⇒ n² – 7n + 6n – 42 = 0
⇒ n(n – 7) + 6(n – 7) = 0
⇒ (n – 7) (n + 6) = 0
⇒ n – 7 = 0 or n + 6 = 0
⇒ n = 7 or n = -6 (reject)
But n (time) can not be negative.
∴ Time taken by policeman to catch the thief
= n – 2 = 7 – 2 = 5 minutes

Question 80.
The houses in a row are numbered conse cutively from 1 to 49. Show that there exists a value of X such that sum of numbers of houses preceding the house numbered X is equal to sum of the numbers of houses following X. (2016OD)
Solution:
Here the A.P. is 1, 2, 3, …., 49
Here a = 1, d = 1, a_n = 49

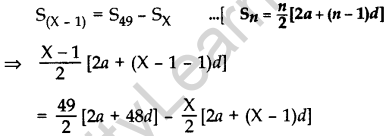
Now,
⇒ (X – 1)² (2 + (X – 2)) = 49(2 + 48) – X[2 + (x – 1)] ⇒ (X – 1). X = 2,450 – X(X + 1)
⇒ x² – X = 2,450 – X² – X
⇒ X² – X + X² + X = 2,450
⇒ 2X² = 2,450
⇒ X² = 1,225
∴ X = \(+\sqrt{1,225}\) = 35 …[X can not be -ve

Question 81.
Find the sum of n terms of the series \(\left(4-\frac{1}{n}\right)+\left(4-\frac{2}{n}\right)+\left(4-\frac{3}{n}\right)+\ldots \ldots .\) (2017D)
Solution:
First term, a = 4 – \(\frac{1}{n}\)