Table of Contents
Trigonometry is an essential branch of mathematics that deals with the relationships between the sides and angles of triangles. It plays a crucial role in various fields, including engineering, navigation, physics, and astronomy. In particular, the trigonometry table is a powerful tool that allows students and professionals to quickly reference the values of trigonometric functions for common angles. This table simplifies the process of solving problems involving sine, cosine, tangent, and other trigonometric ratios.
What is a Trigonometry Table?
A trigonometry table is a systematic arrangement of trigonometric ratios for key angles, typically 0°, 30°, 45°, 60°, and 90°, and their corresponding values for the primary trigonometric functions: sine (sin), cosine (cos), tangent (tan), and their reciprocals like cosecant (cosec), secant (sec), and cotangent (cot).
The table provides quick access to the numerical values of trigonometric functions, making it easier for students to solve various problems in mathematics and applied sciences.
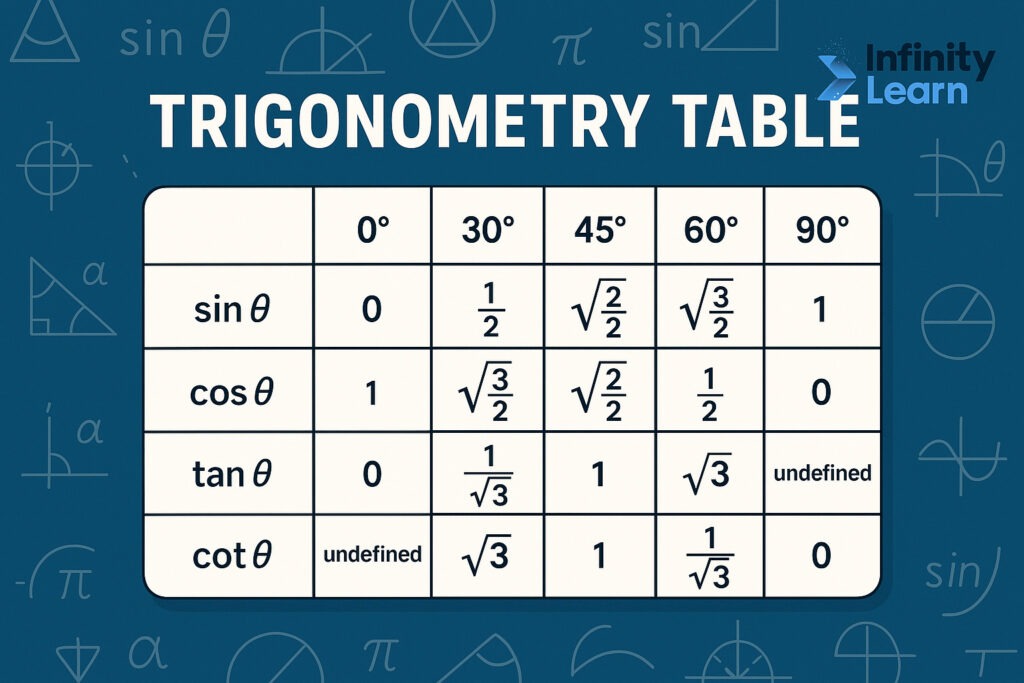
Primary Trigonometric Functions and Ratios
Sine (sin)
Sine is one of the fundamental trigonometric functions. It is defined as the ratio of the opposite side to the hypotenuse in a right-angled triangle. In the context of the unit circle, sine corresponds to the y-coordinate of a point on the circle.
Cosine (cos)
Cosine is another core trigonometric function. It represents the ratio of the adjacent side to the hypotenuse in a right-angled triangle. On the unit circle, it corresponds to the x-coordinate of a point.
Tangent (tan)
Tangent is defined as the ratio of the opposite side to the adjacent side. It can also be expressed as tan(θ) = sin(θ) / cos(θ). The tangent function is widely used in solving problems involving slopes and angles of elevation.
Cotangent (cot)
Cotangent is the reciprocal of the tangent function, defined as cot(θ) = 1 / tan(θ) or cot(θ) = cos(θ) / sin(θ). It is useful in various applications such as geometry and physics.
Secant (sec)
Secant is the reciprocal of cosine, defined as sec(θ) = 1 / cos(θ). It is used in solving problems related to angles and distances.
Cosecant (cosec)
Cosecant is the reciprocal of sine, defined as cosec(θ) = 1 / sin(θ). It is used in various engineering and physics calculations.
Standard Angles in Trigonometry
The most commonly used angles in trigonometry are 0°, 30°, 45°, 60°, and 90°. These angles are critical because their corresponding trigonometric values are easy to memorize and are widely used in mathematical and scientific applications.
Trigonometric Table for Key Angles
| Angle (°) | Sine (sin) | Cosine (cos) | Tangent (tan) | Cosecant (cosec) | Secant (sec) | Cotangent (cot) |
| 0 | 0 | 1 | 0 | Undefined | 1 | Undefined |
| 30 | 0.5 | 0.866 | 0.577 | 2 | 1.154 | 1.732 |
| 45 | 0.707 | 0.707 | 1 | 1.414 | 1.414 | 1 |
| 60 | 0.866 | 0.5 | 1.732 | 1.154 | 2 | 0.577 |
| 90 | 1 | 0 | Undefined | 1 | Undefined | 0 |
Triangle Components and Relationships
1. Hypotenuse
The hypotenuse is the longest side of a right-angled triangle, opposite to the right angle. It plays a crucial role in defining trigonometric ratios.
2. Adjacent Side
The adjacent side is the side next to the given angle (other than the hypotenuse) in a right-angled triangle.
3. Opposite Side
The opposite side is the side opposite the given angle in a right-angled triangle.
4. Pythagorean Theorem
The Pythagorean theorem states that for any right-angled triangle:
Hypotenuse2 = Opposite2 + Adjacent2
This theorem is fundamental to trigonometry and provides a way to calculate the length of a side in a right triangle.
Trigonometric Identities and Formulas
1. Pythagorean Identity
The most important identity in trigonometry is the Pythagorean identity:
sin2(θ) + cos2(θ) = 1
This identity holds for all values of θ and is derived from the unit circle.
2. Reciprocal Identities
The reciprocal identities define relationships between the core trigonometric functions and their reciprocals:
csc(θ) = 1 / sin(θ), sec(θ) = 1 / cos(θ), cot(θ) = 1 / tan(θ)
Applications of Trigonometry
1. Engineering
Trigonometry plays a vital role in civil, mechanical, and electrical engineering. It is used in calculating distances, forces, and angles in designs and construction.
2. Navigation
Trigonometry is critical in navigation systems, including GPS and satellite technology, where trigonometric functions are used to calculate positions and paths.
3. Astronomy
Astronomers use trigonometry to measure the distance between celestial objects and understand their motion. The trigonometric table aids in solving angular distance problems.
4. Sound Waves
In physics, trigonometry is used to model sound waves, with applications in acoustics and audio engineering. The Fourier Transform relies on trigonometric functions to analyze and process sound signals.
5. Surveying
Surveying involves measuring land and mapping distances. Trigonometric tables assist surveyors in calculating angles and distances to create accurate maps.
Tricks to Remember Trigonometry Table
Memorizing the trigonometric values for key angles can be challenging. Here are some tricks to help you remember:
- SOHCAHTOA: This mnemonic helps you remember the definitions of sine, cosine, and tangent:
- Sine = Opposite / Hypotenuse
- Cosine = Adjacent / Hypotenuse
- Tangent = Opposite / Adjacent
- Unit Circle Visualization: Visualize the unit circle to understand how sine and cosine change as the angle increases.
- Use Symmetry: Remember that sine and cosine are periodic functions, meaning their values repeat after every 360°.
The trigonometry table is a vital tool for anyone learning or working with trigonometry. It provides an easy reference for the values of sine, cosine, tangent, and other trigonometric ratios for key angles. By mastering this table, along with the associated trigonometric identities, you will have a strong foundation for solving more complex problems in mathematics and applied sciences.
FAQs About Trigonometric table, Converting angles, and Common Applications
How to remember the trigonometric table?
Break down the table into sections (sine, cosine, tangent). Use mnemonic devices like 'All Students Take Calculus' to remember positive angles. Visual aids such as diagrams and charts also help.
What is the best introduction to trigonometry?
Start with understanding the basic concepts of angles and the unit circle. Then move to the functions (sine, cosine, tangent) and how they relate to real-world problems. Illustrations and simple examples of triangles are very useful at this stage
Why are trigonometric tables important?
They provide quick access to the values of trigonometric functions for angles, making complex calculations faster, especially before calculators were widely available. They help in simplifying problems in fields like engineering, physics, and architecture.
How do I memorize the values in the trigonometric table easily?
Use mnemonic devices (SOHCAHTOA) to remember the relationship between the sides of a triangle. Also, repeatedly practice using the table and applying it to problems to reinforce memory.
How was the trigonometry table invented?
The earliest trigonometric tables were developed by ancient civilizations like the Babylonians and Greeks. They were created to solve astronomical problems and to facilitate navigation. The concept evolved with the work of mathematicians such as Hipparchus and Aryabhata.
Who invented the trigonometric table?
The concept of trigonometry was developed by many ancient scholars. Aryabhata (India) and Hipparchus (Greece) are among the key contributors to the development of early trigonometric tables. The use of tables for sines and cosines became more standardized with the work of Indian mathematicians in the 5th century.
How can we make a trigonometric table?
To create a trigonometric table, you must first define the angle range (typically from 0° to 90°) and calculate the sine, cosine, and tangent for each degree (or finer increments). This requires precise mathematical formulas or the use of a calculator for accurate results. Once the values are calculated, they can be arranged in a table format for easy reference.
What historical significance does the trigonometric table hold?
Trigonometric tables were crucial in the history of mathematics and astronomy, as they allowed early scientists and navigators to perform calculations more efficiently. They were a major advancement before the advent of modern calculators and were fundamental to developments in fields like physics, astronomy, and engineering.
How do I use the trigonometric table for my math exams?
Start by identifying the angle for which you need to find the trigonometric value (e.g., sine, cosine, or tangent). Look up the corresponding value in the table. Use the correct units (degrees or radians) and apply the value in your equation to solve for unknowns.
How accurate are trigonometric tables?
rigonometric tables are highly accurate, but they are limited by the degree of precision (usually up to four decimal places) and the number of increments used in the table. However, for most practical uses, these tables provide sufficient accuracy.
How do I apply the trigonometric table to solve real-life problems?
rigonometric tables can be used in various real-life scenarios like navigation (calculating angles and distances), engineering (structural analysis), and physics (wave behavior and angles of reflection). Use the table to find the appropriate trigonometric values that will help solve the problem's equations.
When should I use the trigonometric table in different mathematical problems?
Use the trigonometric table when solving problems involving right triangles, wave motion, angles of elevation and depression, or when you need to convert between different units of angle measurement. It is especially helpful in geometry, physics, and engineering.
Are there any modern alternatives to using trigonometric tables?
es, modern alternatives include scientific calculators, graphing calculators, and computer software (like MATLAB, Wolfram Mathematical). These tools can compute trigonometric values instantly, making the process much faster and more efficient than manually using a table.
How are calculators replacing trigonometric tables?
Calculators, both physical and digital, have largely replaced trigonometric tables because they can quickly compute trigonometric values for any given angle with greater precision. They can also handle a wide range of other mathematical operations that make them more versatile than static tables.
What are the pros and cons of using trigonometric tables vs. technology?
Pros of Trigonometric Tables: Simple, no need for electricity or batteries, great for understanding the basics of trigonometry. Cons of Trigonometric Tables: Time-consuming, limited to predefined increments, and less precise than modern tools. Pros of Technology: Instant results, high precision, ability to compute for a wide range of angles and functions. Cons of Technology: Requires a device (calculator, computer), potential reliance on technology.
Is it still useful to learn trigonometric tables today?
Yes, learning trigonometric tables can enhance your understanding of trigonometry's fundamental concepts. It helps build a strong foundation for solving complex problems, and it’s beneficial for students who need to work in situations where a calculator might not be available.








