NCERT Solutions – Class 7 Maths Chapter 11 Perimeter and Area Ex 11.3

NCERT Solutions Class 7 Chapter 11 – Perimeter and Area Ex 11.3

The NCERT Solution for Class 7 Maths Chapter 11 Exercise 11.3 is an essential resource tailored to help students grasp the concepts covered in this segment of the curriculum. These NCERT solutions are meticulously crafted in alignment with the CBSE syllabus, ensuring that every problem is approached with methods that both simplify learning and enhance comprehension. This exercise gets into important mathematical principles that are fundamental at this stage of education, providing detailed step-by-step solutions that aid students in effectively navigating through their NCERT textbook. By utilizing these NCERT solutions for class 7, students can confidently tackle the challenges presented in the exercise, reinforcing their mathematical skills and preparing them for more advanced topics. Get NCERT Solutions for Class 7 Maths Chapter 11 Perimeter and Area on Infinity Learn for free.

CBSE Class 7 Maths Syllabus

NCERT Solution for Class 7 Maths Chapter 11 Exercise 11.3 Questions Answers

Here are all Class 7 maths chapter 11 exercise 11.3 questions with simple and easy solutions

Ex 11.3 Class 7 Maths Question 1.

Find the circumference of the circles with the following radius. (Take π =\(\frac{22}{7}\))
(a) 14 cm
(b) 28 mm
(c) 21 cm
Solution:
(a) Given: Radius (r) = 14 cm
∴ Circumference = 2πr = 2 × \(\frac{22}{7}\) × 14
= 88 cm
(b) Given: Radius (r) = 28 mm
∴ Circumference = 2πr = 2 × \(\frac{22}{7}\) × 28
= 176 mm
(c) Given: Radius (r) = 21 cm
∴ Circumference = 2πr = 2 × \(\frac{22}{7}\) × 21
= 132 cm

Ex 11.3 Class 7 Maths Question 2.

Find the area of the following circles, given that (Take π =\(\frac{22}{7}\))
(a) radius = 14 mm
(b) diameter = 49 m
(c) radius = 5 cm
Solution:
(a) Here, r = 14 mm
∴ Area of the circle = πr²
= π × 14 × 14 = \(\frac{22}{7}\) × 14 × 14
(b) Here, diameter = 49 m 49

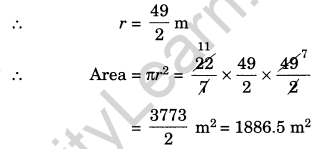
(c) Here, radius = 5 cm

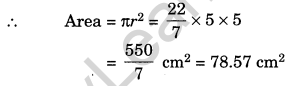
Ex 11.3 Class 7 Maths Question 3.

If the circumference of a circular sheet is 154 m, find its radius. Also find the area of the sheet. (Take π =\(\frac{22}{7}\))
Solution:
Given: Circumference = 154 m
∴ 2πr = 154

Ex 11.3 Class 7 Maths Question 4.

A gardener wants to fence a circular garden of diameter 21 m. Find the length of the rope he needs to purchase, if he makes 2 rounds offence. Also find the cost of the rope, if it costs ₹ 4 per metre. (Take π =\(\frac{22}{7}\))

Solution:
Diameter of the circular garden = 21 m
∴ Radius = \(\frac{21}{2}\) m
∴ Circumference = 2πr = \(2 \times \frac{22}{7} \times \frac{21}{2}\)
= 66 m
Length of rope needed for 2 rounds
= 2 × 66 m = 132 m
Cost of the rope = ₹4 × 132 = ₹ 528

Ex 11.3 Class 7 Maths Question 5.

From a circular sheet of radius 4 cm, a circle of radius 3 cm is removed. Find the area of the remaining sheet. (Take π = 3.14)
Solution:
Radius of the circular sheet = 4 cm
∴ Area = πr² = π × 4 × 4 = 16π cm²
Radius of the circle to be removed = 3 cm
∴ Area of sheet removed = πr² = 9π cm²
Area of the remaining sheet
= (16π – 9π) cm2 = 7π cm²
= 7 × 3.14 cm² = 21.98 cm²
Hence, the required area = 21.98 cm².

Ex 11.3 Class 7 Maths Question 6.

Saima wants to put a lace on the edge of a circular table cover of diameter 1.5 m. Find the length of the lace required and also find its cost if one metre of the lace costs ₹ 15. (Take π = 3.14)
Solution:
Diameter of the table cover = 1.5 m
∴ Radius = \(\frac{1.5}{2}\) = 0.75 m
∴ Length of the lace = 2πr = 2 × 3.14 × 0.75
= 4.710 m
Cost of the lace = ₹ 15 × 4.710 = ₹ 70.65

Ex 11.3 Class 7 Maths Question 7.

Find the perimeter of the given figure, which is a semicircle including its diameter.

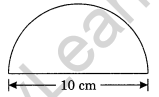
Solution:
Given: Diameter = 10 cm

Hence, the required perimeter
= 25.7 cm. (approx.)

Ex 11.3 Class 7 Maths Question 8.

Find the cost of polishing a circular table-top of diameter 1.6 m, if the rate of polishing is ₹ 15 m². (Take π = 3.14)
Solution:
Given:
Diameter = 1.6 m
∴ Radius = \(\frac{1.6}{2}\) = 0.8 m
Area of the table-top = πr²
= 3.14 × 0.8 × 0.8 m²
= 2.0096 m²
∴ Cost of polishing = ₹ 15 × 2.0096
= ₹ 30.14 (approx.)

Ex 11.3 Class 7 Maths Question 9.

Shazli took a wire of length 44 cm and bent it into the shape of a circle. Find the radius of that circle. Also find its area. If the same wire is bent into the shape of a square, what will be the length of each of its sides? Which figure encloses more area, the circle or the square? (Take π =\(\frac{22}{7}\))
Solution:
Length of the wire to be bent into a circle = 44 cm
2πr = 44

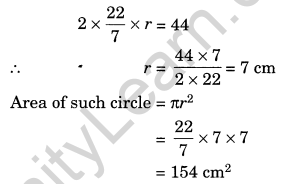
Now, the length of the wire is bent into a square.
Here perimeter of square
= Circumference of line k
Length of each side of the square
\(=\frac{\text { Perimeter }}{4}=\frac{44}{4}=11 \mathrm{cm}\)
Area of the square = (Side)² = (11)² = 121 cm²
Since, 154 cm² >121 cm²
Thus, the circle encloses more area.

Ex 11.3 Class 7 Maths Question 10.

From a circular card sheet of radius 14 cm, two circles of radius 3.5 cm and a rectangle of length 3 cm and breadth 1 cm are removed, (as shown in the given figure below). Find the area of the remaining sheet. (Take π = \(\frac{22}{7}\))

Solution:
Radius of the circular sheet = 14 cm
∴ Area = πr² = \(\frac{22}{7}\) × 14 × 14 cm²
= 616 cm²
Area of 2 small circles = 2 × πr²
= 2 × \(\frac{22}{7}\) × 3.5 × 3.5 cm²
= 77.0 cm²
Area of the rectangle = l × b
= 3 × 1 cm² = 3 cm²
Area of the remaining sheet after removing the 2 circles and 1 rectangle
= 616 cm² – (77 + 3) cm²
= 616 cm² – 80 cm² = 536 cm²

Ex 11.3 Class 7 Maths Question 11.

A circle of radius 2 cm is cut out from a square piece of an aluminium sheet of side 6 cm. What is the area of the left over aluminium sheet? (Take π = 3.14)
Solution:
Side os the square sheet = 6 m
∴ Area of the sheet = (Side)² = (6)² = 36 cm²
Radius of the circle = 2 cm
∴ Area of the circle to be cut out = πr²
= \(=\frac{22}{7} \times 2 \times 2=\frac{88}{7} \mathrm{cm}^{2}\)
Area of the left over sheet

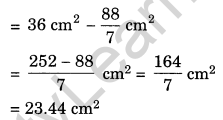
Ex 11.3 Class 7 Maths Question 12.

The circumference of a circle is 31.4 cm. Find the radius and the area of the circle. (Take π = 3.14)
Solution:
Circumference of the circle = 31.4 cm
2πr = 31.4
∴ \(r=\frac{31.4}{2 \times 3.14}\) = 5cm
Area of the circle = 7πr² = 3.14 × 5 × 5 = 78.5 cm²
Hence, the required radius = 5 cm and area = 78.5 cm².

Ex 11.3 Class 7 Maths Question 13.

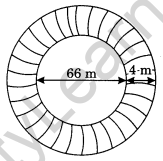
A circular flower bed is surrounded by a path 4 m wide. The diameter of the flower bed is 66 m. What is the area of this path? (Take π = 3.14)

Solution:
Diameter of the flower bed = 66 m .
∴ Radius = \(\frac{66}{2}\) = 33 m
Let r₁ = 33 m
Width of the path = 4 m
Radius of the flower bed included path
= 33 m + 4 m = 37m
Let r₂ = 37m
Area of the circular path = \(\pi\left(r_{2}^{2}-r_{1}^{2}\right)\)
= 3.14 (37²– 33²)
= 3.14 × (37 + 33) (37 – 33) [Y a² – b² = (a + b)(a-b)] = 3.14 × 70 × 4 = 879.20 m²
Hence, the required area = 879.20 m²

Ex 11.3 Class 7 Maths Question 14.

A circular flower garden has an area of 314 m². A sprinkler at the centre of the garden can cover an area that has a radius of 12 m. Will the sprinkler can water the entire garden?
[Take π = 3.14] Solution:
Area of the flower garden = 314 m²
Radius of the circular portion covered by the sprinkler = 12 m
∴ Area = 7πr² = 3.14 × 12 × 12
= 3.14 × 144 m² = 452.16 m²
Since 452.16 m² > 314 m²
Yes, the sprinkler will water the entire garden.

Ex 11.3 Class 7 Maths Question 15.

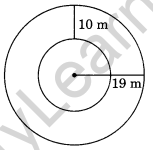
Find the circumference of the inner and the outer circles, shown in the given figure. (Take π = 3.14)

Solution:
Radius of the outer circle = 19 m
∴ Circumference of the outer circle = 2πr
= 2 × 3.14 × 19 = 3.14 × 38 m
= 119.32 m
Radius of the inner circle
= 19m – 10m = 9m
∴ Circumference = 2πr = 2 × 3.14 × 9
= 56.52 m
Here the required circumferences are 56.52 m and 119.32 m.

Ex 11.3 Class 7 Maths Question 16.

How many times a wheel of radius 28 cm must rotate to go 352 m? (Take π = \(\frac{22}{7}\))
Solution:
Radius of the wheel = 28 cm
∴ Circumference = 2πr = 2 × \(\frac{22}{7}\) × 28 = 176 cm
Number of rotations made by the wheel in going 352 m or 35200 cm
\(=\frac{35200}{176}=200\)
Hence, the required number of rotation = 200.

Ex 11.3 Class 7 Maths Question 17.

The minute hand of a circular clock is 15 cm long. How far does the tip of the minute hand move in 1 hour? (Take π = 3.14)
Solution:
Length of minute hand = 15 cm
∴ Radius = 15 cm
Circumference = 2πr
= 2 × 3.14 × 15 cm = 94.2 cm
Since the minute hand covers the distance in 1 hour equal to the circumference of the circle. Here the required distance covered by the minute hand = 94.2 cm.

Also Check:

• Class 7 Maths NCERT Solutions Exercise 11.1
• Class 7 Maths NCERT Solutions Exercise 11.2
• Class 7 Maths NCERT Solutions Exercise 11.3
• Class 7 Maths NCERT Solutions Exercise 11.4

NCERT Solution for Class 7 Maths Chapter 11 Exercise 11.3 PDF Download

You can easily get the NCERT Solution for Class 7 Maths Chapter 11 Exercise 11.3 in PDF format. It’s great because you can download it and use it whenever you want, which makes studying and reviewing easier. This NCERT solutions PDF has detailed explanations and step-by-step solutions to help you understand better and prepare for exams. It’s a valuable resource that can boost your math skills.

NCERT Solutions for Class 7 Maths Chapter-wise PDF

• Chapter 1 Integers
• Chapter 2 Fractions and Decimals
• Chapter 3 Data Handling
• Chapter 4 Simple Equations
• Chapter 5 Lines and Angles
• Chapter 6 The Triangles and Its Properties
• Chapter 7 Congruence of Triangles
• Chapter 8 Comparing Quantities
• Chapter 9 Rational Numbers
• Chapter 10 Practical Geometry
• Chapter 11 Perimeter and Area
• Chapter 12 Algebraic Expressions
• Chapter 13 Exponents and Powers
• Chapter 14 Symmetry
• Chapter 15 Visualizing Solid Shapes

FAQs on NCERT Solution for Class 7 Maths Chapter 11 Exercise 11.3

Where to download NCERT solution for Class 7 Maths Chapter 11 Exercise 11.3?

Where to download NCERT solution for Class 7 Maths Chapter 11 Exercise 11.3?

What is the perimeter and area of a parallelogram in Class 7?

What is the perimeter and area of a parallelogram in Class 7?

How do you find the perimeter in Class 7?

To find the perimeter in Class 7, add up the lengths of all the sides of the given shape or figure. For example, in a rectangle, you add the lengths of all four sides.

What is the name of Chapter 11 of Class 7 Maths?

Chapter 11 of Class 7 Maths is titled Perimeter and Area, focusing on concepts related to calculating the perimeter and area of various geometric shapes.

What is the formula for a parallelogram?

The formula for the area of a parallelogram is base multiplied by height, while the formula for the perimeter involves adding the lengths of all four sides of the parallelogram.

What is the area of a parallelogram in Class 7?

In Class 7, the area of a parallelogram is calculated by multiplying the base and the height of the parallelogram, providing the measure of space enclosed within its boundaries.