Table of Contents
In mathematics, a circle is a specific type of ellipse with an eccentricity of zero, meaning its two foci coincide. It’s defined as the set of points equidistant from its center. The distance from the center to the circle’s edge is called the radius, while the diameter is twice the radius, dividing the circle in half.
A circle is a fundamental 2D shape measured by its radius. It divides the plane into interior and exterior regions, resembling a curved line segment when bent to form a closed loop.
This 2D figure has both area and perimeter. The perimeter, also known as the circumference, is the distance around the circle, while the area is the space enclosed by it in a 2D plane. These circle properties and formulas are important in mathematics and geometry.
Circle Definition
A circle is a closed two-dimensional shape where all points on the plane are equally distant from a central point called the ‘center.’ Any line passing through the circle acts as a line of reflection symmetry, and the circle exhibits rotational symmetry for any angle. The formula for a circle in a plane is expressed as follows:
(x-h)2 + (y-k)2 = r2
where,
- (x,y) are the coordinate points
- (h,k) is the coordinate of the centre of a circle
- r is the radius of a circle.
Types of circle
In Mathematics, there are several types of circles and related concepts:
- Standard Circle: A standard circle is the most common type, with a fixed center and radius.
- Concentric Circles: These are multiple circles that share the same center point but have different radii.
- Tangent Circles: Tangent circles touch each other at exactly one point from the outside.
- Secant Circle: A secant circle intersects another circle at two distinct points.
- Inscribed Circle: An inscribed circle is the largest possible circle that can fit inside a polygon, touching all sides of the polygon.
- Circumcircle: A circumcircle is the smallest circle that can enclose a polygon, touching all its vertices.
- Unit Circle: A unit circle has a radius of 1 unit and is often used in trigonometry.
- Degenerate Circle: This is a circle with a radius of 0, essentially a single point.
- Hollow Circle: A hollow circle is just the boundary without any filled interior.
- Ellipse: An ellipse is a stretched or compressed circle, where the distance between the two foci is greater than the length of the major axis.
- Arc: An arc is a segment of a circle’s circumference.
- Semicircle: A semicircle is half of a full circle, consisting of an arc and the diameter it is based on.
- Quarter Circle: A quarter circle is one-fourth of a full circle, formed by cutting a circle into four equal parts.
How to Draw a Circle?
In this Class 10 math project focusing on circles, we provide a comprehensive explanation of circle construction, properties, and terminology. To grasp the concept of circles in a straightforward manner, explore the Class 10 circle project and engage in the following exercise:
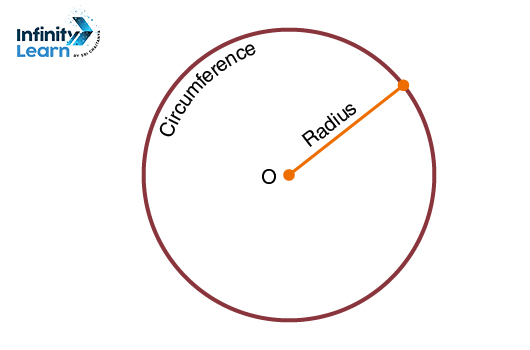
Begin with a blank sheet of paper and designate a central point, which we’ll call point O. Choose any random radius length, such as 3 cm. Using a ruler, measure 3 cm in various directions from point O, marking these points precisely 3 cm away from the central point. Feel free to mark as many points as desired, but maintain the 3 cm distance from point O in all directions.
Also Check
- Regions of a Circle
- Circumference of a Circle
- Chords of a Circle
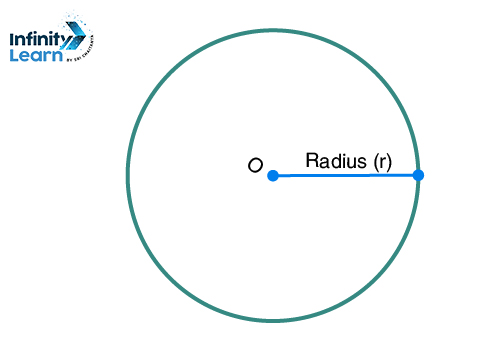
Radius of Circle (r)
A line segment that links the center of a circle to any point on its circumference is referred to as a ‘radius.’ This distance is typically denoted by the symbol ‘R’ or ‘r’ in mathematical notation.
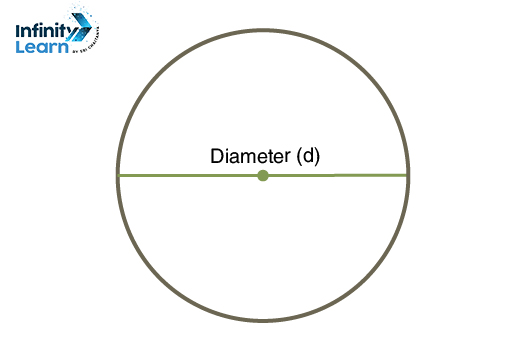
Diameter (d) of Circle
A line segment with both endpoints on a circle is called a diameter. The diameter is always twice the length of the radius, expressed as d = 2r. Similarly, you can find the radius of the circle by using the formula r = d/2, which derives from the diameter.
Properties of Circle
- The circumference of a circle is uniformly distant from its center.
- A circle diameter divides it into two equal halves.
- Circles with identical radii are considered congruent.
- Circles that vary in size or have distinct radii are considered similar.
- The circle diameter serves as its longest chord and is precisely twice the length of the radius.









