MCQs for Class 12 Maths Chapter 2: Inverse Trigonometric Functions are provided here with correct answers and detailed solutions. These MCQs cover key concepts such as domain and range restrictions of trigonometric functions, essential for understanding their inverses and behavior graphically. They are aligned with the latest CBSE guidelines for the 2023-2024 board exams, offering valuable preparation material for Class 12 students. Access MCQs for all Class 12 Maths chapters with solutions here.
Inverse Trigonometric Functions Class 12 Maths MCQs Pdf
Question 1. Solve for x : {xcos(cot-1 x) + sin(cot-1 x)}2 = \(\frac{51}{50}\)
(a) \(\frac{1}{\sqrt{2}}\)
(b) \(\frac{1}{5 \sqrt{2}}\)
(c) 2√2
(d) 5√2
Answer: (b) \(\frac{1}{5 \sqrt{2}}\)
Question 2.
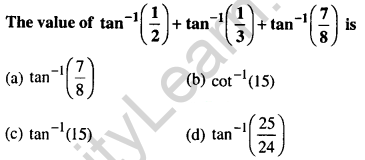
Answer: (c) tan-1(15)
Question 3.
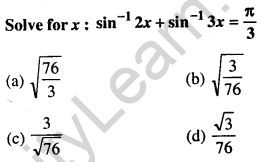
Answer: (b) \(\sqrt{\frac{3}{76}}\)
Question 4.
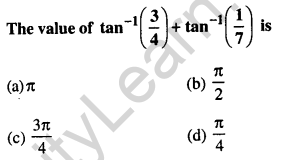
Answer: (d) \(\frac{\pi}{4}\)
Also Refer: Areas Related to Circle Class 10 MCQs
Question 5. If sin-1(x2 – 7x + 12) = nπ, ∀ n ∈ I, then x =
(a) -2
(b) 4
(c) -3
(d) 5
Answer: (b) 4
Question 6. If cos-1 x + sin-1 x = π, then the value of x is
(a) \(\frac{3}{2}\)
(b) \(\frac{1}{\sqrt{2}}\)
(c) \(\frac{\sqrt{3}}{2}\)
(d) \(\frac{2}{\sqrt{3}}\)
Answer: (c) \(\frac{\sqrt{3}}{2}\)
Question 7. If sin-1 x – cos-1 x = \(\frac{\pi}{6}\), then x =
(a) \(\frac{1}{2}\)
(b) \(\frac{\sqrt{3}}{2}\)
(c) \(-\frac{1}{2}\)
(d) \(-\frac{\sqrt{3}}{2}\)
Answer: (b) \(\frac{\sqrt{3}}{2}\)
Question 8. If tan-1 (cot θ) = 2θ, then θ is equal to
(a) \(\frac{\pi}{3}\)
(b) \(\frac{\pi}{4}\)
(c) \(\frac{\pi}{6}\)
(d) None of these
Answer: (c) \(\frac{\pi}{6}\)
Click Here: CBSE Class 12 Syllabus 2024
Question 9. cot(\(\frac{\pi}{4}\) – 2cot-1 3) =
(a) 7
(b) 6
(c) 5
(d) None of these
Answer: (a) 7
Question 10. If tan-1 3 + tan-1 x = tan-1 8, then x =
(a) 5\
(b) \(\frac{1}{5}\)
(c) \(\frac{5}{14}\)
(d) \(\frac{14}{5}\)
Answer: (b) \(\frac{1}{5}\)
Question 11.

Answer: (d) \(-\frac{\pi}{6}\)
Question 12.

Answer: (b) \(\frac{\pi}{3}\)
Question 13.

Answer: (b) \(\frac{\pi}{3}\)
Question 14.

Answer: (a) \(\frac{\pi}{4}\)
Question 15.
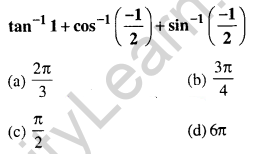
Answer: (b) \(\frac{3 \pi}{4}\)
Question 16.
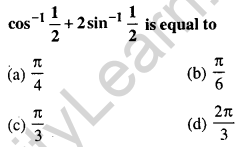
Answer: (d) \(\frac{2 \pi}{3}\)
Question 17.
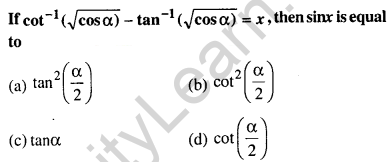
Answer: (a) \(\tan ^{2}\left(\frac{\alpha}{2}\right)\)
Question 18.
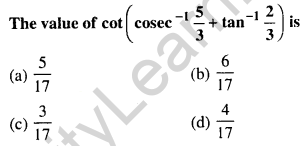
Answer: (b) \(\frac{6}{17}\)
Question 19. If tan-1 (x – 1) + tan-1 x + tan-1 (x + 1) = tan-1 3x, then the values of x are
(a) \(\pm \frac{1}{2}\)
(b) 0, \(\frac{1}{2}\)
(c) 0, \(-\frac{1}{2}\)
(d) 0, \(\pm \frac{1}{2}\)
Answer: (d) 0, \(\pm \frac{1}{2}\)
Question 20. If 6sin-1 (x2 – 6x + 8.5) = π, then x is equal to
(a) 1
(b) 2
(c) 3
(d) 8
Answer: (b) 2
Question 21.
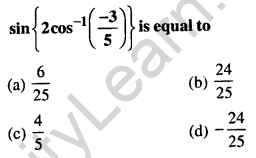
Answer: (d) \(-\frac{24}{25}\)
Question 22. sin-1 (1 – x) – 2sin-1 x = \(\frac{\pi}{2}\)
(a) 0
(b) 1/2
(c) 0, 1/2
(d) -1/2
Answer: (a) 0
Question 23. 2tan-1(cos x) = tan-1(2cosec x)
(a) 0
(b) π/3
(c) π/4
(d) π/2
Answer: (c) π/4
Question 24.

Answer: (a) \(\sqrt{\frac{x^{2}+1}{x^{2}+2}}\)
Question 25.

Answer: (a) \(\frac{3 \pi}{5}\)
Question 26. The domain of the function defind by f(x) = \(\sin ^{-1} \sqrt{x-1}\) is
(a) [1, 2]
(b) [-1, 1]
(c) [0, 1]
(d) none of these
Answer: (a) [1, 2]
Question 27. The value of sin (2tan-1 (0.75)) is equal to
(a) 0.75
(b) 1.5
(c) 0.96
(d) sin 1.5
Answer: (c) 0.96
Question 28. The value of expression 2 sec-1 2 + sin-1(\(\frac{1}{2}\))
(a) \(\frac{\pi}{6}\)
(b) \(\frac{5 \pi}{6}\)
(c) \(\frac{7 \pi}{6}\)
(d) 1
Answer: (b) \(\frac{5 \pi}{6}\)
Question 29.
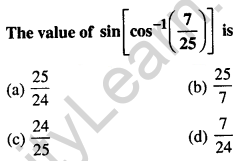
Answer: (c) \(\frac{24}{25}\)
Question 30. The value of the expression \(\tan \left(\frac{1}{2} \cos ^{-1} \frac{2}{\sqrt{3}}\right)\)
(a) 2 + √5
(b) √5 – 2
(c) \(\frac{\sqrt{5}+2}{2}\)
(d) 5 + √2
Answer: (b) √5 – 2
Question 31.

Answer: (a) \(\frac{6}{17}\)
Question 32.
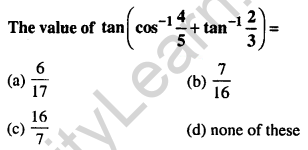
Answer: (d) none of these
Question 33.
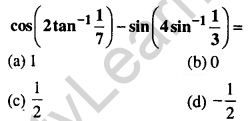
Answer: (b) 0
Question 34.
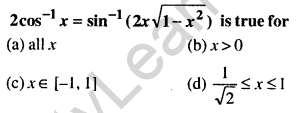
Answer: (d) \(\frac{1}{\sqrt{2}} \leq x \leq 1\)
Question 35. cos-1[cos(2cot-1(√2 – 1))] = ______
(a) √2 – 1
(b) 1 + √2
(c) \(\frac{\pi}{4}\)
(d) \(\frac{3 \pi}{4}\)
Answer: (d) \(\frac{3 \pi}{4}\)
Question 36. The range of sin-1 x + cos-1 x + tan-1 x is
(a) [0, π]
(b) \(\left[\frac{\pi}{4}, \frac{3 \pi}{4}\right]\)
(c) (0, π)
(d) \(\left[0, \frac{\pi}{2}\right]\)
Answer: (b) \(\left[\frac{\pi}{4}, \frac{3 \pi}{4}\right]\)
Question 37.

Answer: (c) \(\frac{\pi}{4}\)
Question 38. Find the value of sec2 (tan-1 2) + cosec2 (cot-1 3)
(a) 12
(b) 5
(c) 15
(d) 9
Answer: (c) 15
Question 39.
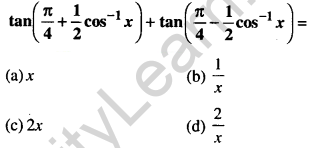
Answer: (d) \(\frac{2}{x}\)
Question 40. The equation sin-1 x – cos-1 x = cos-1(\(\frac{\sqrt{3}}{2}\)) has
(a) unique solution
(b) no solution
(c) infinitely many solution
(d) none of these
Answer: (a) unique solution
Question 41. 3 tan-1 a is equal to

Answer: (d) \(\tan ^{-1}\left(\frac{3 a-a^{3}}{1-3 a^{2}}\right)\)
Question 42.
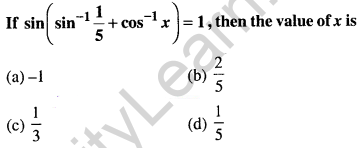
Answer: (d) \(\frac{1}{5}\)
Question 43. The equation 2cos-1 x + sin-1 x = \(\frac{11 \pi}{6}\) has
(a) no solution
(b) only one solution
(c) two solutions
(d) three solutions
Answer: (a) no solution
Question 44.
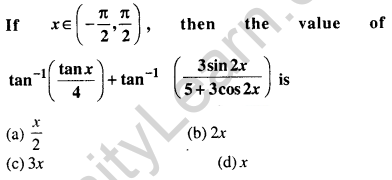
Answer: (d) x
Question 45. If tan-1 2x + tan-1 3x = \(\frac{\pi}{4}\), then x is
(a) \(\frac{1}{6}\)
(b) 1
(c) (\(\frac{1}{6}\), -1)
(d) none of these
Answer: (a) \(\frac{1}{6}\)
Question 46.
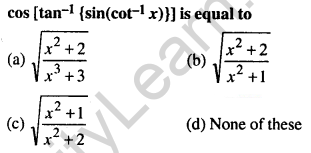
Answer: (c) \(\sqrt{\frac{x^{2}+1}{x^{2}+2}}\)
Question 47.
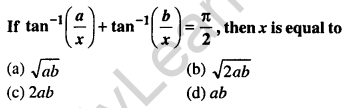
Answer: (a) \(\sqrt{a b}\)
Question 48. If tan-1 x – tan-1 y = tan-1 A, then A is equal to
(a) x – y
(b) x + y
(c) \(\frac{x-y}{1+x y}\)
(d) \(\frac{x+y}{1-x y}\)
Answer: (c) \(\frac{x-y}{1+x y}\)
Question 49.
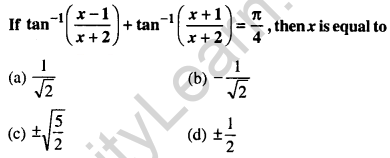
Answer: (c) \(\pm \sqrt{\frac{5}{2}}\)
Question 50. The value of cot-1 9 + cosec-1(\(\frac{\sqrt{41}}{4}\)) is given by
(a) 0
(b) \(\frac{\pi}{4}\)
(c) tan-1 2
(d) \(\frac{\pi}{2}\)
Answer: (b) \(\frac{\pi}{4}\)





