Table of Contents
Boyle’s law, a fundamental principle in the study of gases, describes the relationship between the volume and pressure of a gas. This law was initially observed by Henry Power and Towneley, who noticed the correlation between these two variables.
Building upon their observations, Robert Boyle, a renowned Anglo-Irish physicist, philosopher, and chemist, conducted further experiments to solidify this discovery. In 1662, Boyle published the results of his experiments, thereby formalizing Boyle’s law and contributing significantly to our understanding of gas behavior.
What is Boyle’s Law?
Boyle’s law, first formulated by the Anglo-Irish chemist Robert Boyle in 1662, elucidates a fundamental relationship between the pressure and volume of a gas. It asserts that when the temperature and quantity of gas remain constant, the pressure exerted by the gas is inversely proportional to the volume it occupies.
In simpler terms, if you squeeze a gas into a smaller space, its pressure will rise, and conversely, if you allow it to expand into a larger space, its pressure will decrease.
When dealing with a gas, the connection between its volume and pressure (while keeping the mass and temperature constant) can be described using mathematical equations.
P ∝ (1/V)
When a gas exerts pressure (P) and occupies a volume (V), this relationship can be turned into an equation by including a constant value, known as ‘k.
P = k*(1/V) ⇒ PV = k
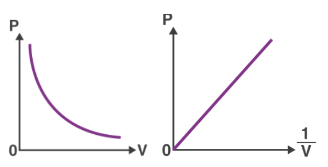
Below is a visual representation of how the relationship between pressure and volume changes for a set amount of gas when the temperature remains constant.
Boyle’s Law Graph
When you plot the pressure of a gas (P) against the inverse of its volume (1/V), you get a straight line.
Boyle’s Law Formula and Derivations
Boyle’s law explains how changes in gas volume affect its pressure when the quantity and temperature stay constant. Simply put, if you squeeze a gas into a smaller space, its pressure goes up, and if you let it expand into a larger space, its pressure goes down. Mathematically, it’s represented as:
P1V1 = P2V2
Where:
P1 is the initial pressure of the gas
V1 is the initial volume of the gas
P2 is the final pressure of the gas
V2 is the final volume of the gas
This idea stems from Boyle’s law, which describes the relationship between pressure and volume in a gas. Boyle’s law states that for a given amount of gas at a steady temperature, the product of its pressure and volume remains constant (PV = k). So, in simpler terms,
P1V1 = k (initial pressure * initial volume)
P2V2 = k (final pressure * final volume)
∴ P1V1 = P2V2
This equation comes from Boyle’s law, which states that for a fixed amount of gas at a constant temperature, the product of pressure and volume always equals a constant, represented by ‘k’. So, whether you’re looking at the beginning or end of a change in volume, the pressure and volume together will always equal that same constant.
In practical terms, this equation helps us understand how pressure changes in a gas-filled container when the volume changes, as long as the temperature and quantity of gas remain constant.
Boyle’s Law Example
When you compress a filled balloon by squeezing it, the air trapped inside occupies less space, leading to an increase in pressure according to Boyle’s law. With continued squeezing, the pressure builds up until the balloon eventually bursts.
Similarly, when a scuba diver ascends rapidly from the depths of the ocean towards the water’s surface, the decreasing pressure causes the gas molecules within their body to expand. This expansion of gases can inflict harm on the diver’s internal organs and, in severe cases, may result in fatality. This physiological response aligns with Boyle’s law.
Another instance of this principle at work is observed in deep-sea fish, which perish upon reaching the surface due to the expansion of dissolved gases in their bloodstream.
Boyle’s Law Facts and Characteristics
- Boyle’s Law is all about the relationship between gas volume and pressure. Simply put, when you squash a gas into a smaller space, its pressure shoots up. On the flip side, if you let the gas spread out into a larger space, its pressure drops. This only happens when everything else stays the same.
- Now, Boyle’s Law works best for something called “ideal gases.” These gases are like the superheroes of the gas world—they always follow the rules perfectly. But in real life, no gas is truly ideal. Still, many gases come pretty close under normal conditions.
- But here’s the catch: Boyle’s Law only works when you keep two things constant—temperature and the amount of gas you have. If you mess with these, you’ll need to bring in other gas laws to explain what’s going on.
- When you plot Boyle’s Law on a graph, you get a curvy line that looks like a stretched-out “U.” This line shows that as you make the gas take up more space, its pressure goes down, and vice versa. But no matter where you are on the line, if you multiply the pressure by the volume, you always get the same number, as long as the temperature and amount of gas stay the same.
Boyle’s Law Applications
- Syringe Use: Ever noticed how a syringe works? Well, it’s all about Boyle’s Law. When we pull the plunger, the space inside the barrel increases, reducing pressure. This change in pressure allows external fluids to enter the barrel more easily.
- Bicycle Pumps: Just like syringes, bicycle pumps follow Boyle’s Law. When you pump air, you’re essentially changing the volume inside the pump, affecting its pressure.
- Breathing: Boyle’s Law even plays a role in something as essential as breathing. As we inhale, our lungs expand, lowering pressure inside them. This decrease in pressure allows air from outside to rush in. Exhalation works in the opposite way: the volume decreases, pushing air out.
- Occupational Uses: Boyle’s Law isn’t just for science experiments; it’s practical too. Think of scuba divers and astronauts—whether underwater or in space, understanding Boyle’s Law is crucial for their safety.
Boyle’s Law Solved Examples
Exercise 1:
A gas occupies a volume of 500 mL at a pressure of 800 mmHg. If the volume is decreased to 250 mL while keeping the temperature constant, what will be the new pressure?
Solution:
According to Boyle’s Law:
P1V1 = P2V2
Where:
P1 = Initial pressure (800 mmHg)
V1 = Initial volume (500 mL)
P2 = Final pressure (to be determined)
V2 = Final volume (250 mL)
800*500 = P2*250
400,000 = 250*P2
P2 = 400,000/250 = 1600 mmHg
So, the new pressure will be 1600 mmHg.
Exercise 2:
A gas at 2 atm pressure occupies a volume of 4 L. If the pressure is increased to 3 atm while keeping the temperature constant, what will be the new volume?
Solution:
Again, using Boyle’s Law:
P1V1 = P2V2
Where:
P1 = Initial pressure (2 atm)
V1 = Initial volume (4 L)
P2 = Final pressure (3 atm)
V2 = Final volume (to be determined)
2* 4 = 3 *V2
8 = 3 *V2
V2 = 8/3 = 2.67 L.
So, the new volume will be 2.67 L.
These exercises illustrate how Boyle’s Law can be used to relate the pressure and volume of a gas under constant temperature conditions.
FAQs on Boyle’s Law
What is Boyle’s Law?
Boyle’s Law describes the relationship between the volume and pressure of a gas at constant temperature. It states that as the volume of a gas decreases, its pressure increases proportionally, and vice versa
What is the formula for Boyle’s Law?
Boyle’s Law is expressed as P1V1 = P2V2, where P1 and V1 represent the initial pressure and volume, and P2 and V2 denote the final pressure and volume after a change.
What are the conditions for Boyle’s Law?
Boyle’s Law holds true when the temperature and the quantity of gas remain constant, allowing only changes in volume and pressure to be considered.
What are some practical applications of Boyle’s Law?
Boyle’s Law is applied in various fields such as medicine (syringe use), sports (bicycle pumps), and safety (scuba diving). Understanding this law helps in predicting and managing pressure changes in gas-filled systems.
How does Boyle’s Law affect divers?
Boyle’s Law plays a crucial role in scuba diving, as changes in pressure during ascent and descent can cause gas expansion in the body, leading to decompression sickness. Divers follow strict protocols to prevent such complications and ensure their safety underwater.








