Table of Contents
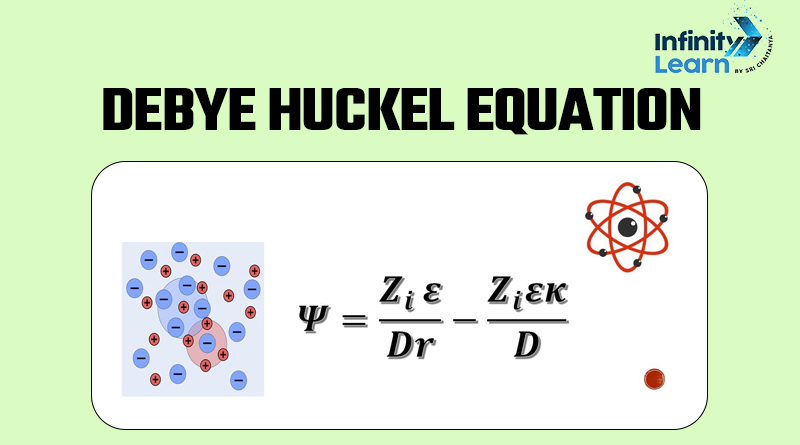
The Debye-Huckel equation is a mathematical formula created to help us understand how things behave in solutions with charged particles, like salts. It helps us see how these charged particles interact with each other, and this interaction is why dilute salt solutions act differently from what we call ‘ideal solutions’.
Entropy, not enthalpy, is what causes solutions to mix. In ideal gases, particles don’t interact, but ideal solutions assume they do. Without these interactions, the solution wouldn’t be in a liquid state. Ideal solutions have zero enthalpy of mixing or solution (ΔHmixing or ΔHsolution = 0).
Interactions in a mixture (A-B) are calculated by adding A-A and B-B interactions. In ideal solutions, the average A-A and B-B interactions are similar, making A-B interactions indistinguishable from A-A/B-B interactions.
In chemistry and biology, A-B interactions aren’t always the same as A or B alone, so the enthalpy of mixing isn’t zero. This led to a new concept: effective concentration (a1), considering deviations from ideal behavior, where the ideal solution equals one.
To convert from mole fraction (x1) to activity (a1), we use an activity coefficient (1).
a1 = y1 x1
Debye Huckel Theory
This theory, known as the Debye-Huckel theory, is all about electrochemistry. It was developed by Peter Debye and Eric Huckel to explain why electrolytic solutions behave differently from what we’d expect in ideal situations.
In ideal solutions, things like how much a substance dissolves are directly related to how much of it is in the solution. But real solutions don’t follow this simple rule. In real solutions, we can’t just look at the concentration of the substance alone. We have to consider something called “activity,” which we represent with the letter ‘a.’
So, we can say that this activity ‘a’ is linked to the concentration ‘c.’ In other words, ‘a’ is equal to ‘gamma’ (represented by the Greek letter) times ‘c,’ where ‘gamma’ is the activity coefficient.
For a perfect ideal solution, the value of ‘gamma’ is 1. When we’re dealing with very diluted solutions, they behave almost ideally. However, concentrated solutions don’t behave this way, and that’s when we see this departure from ideality.
Now, when we’re talking about electrolytic solutions, we know that strong electrolytes tend to break down into positively charged ions (cations) and negatively charged ions (anions). Since opposite charges attract, these ions tend to gather close to each other, and they aren’t just randomly spread out in the solution like they would be in an ideal case.
Here’s the tricky part: we can’t easily measure the activity coefficient of a single ion. So, we calculate something called the mean activity coefficient using formulas.
The Debye-Huckel theory helps us figure out the activity coefficient of a single ion, and it tells us that the departure from ideality happens because of the electric interactions between these ions.
To put it simply, in real solutions, anions (negative ions) are more likely to be found near cations (positive ions), and vice versa. This is why real solutions don’t behave exactly like we’d expect in ideal situations.
Debye Huckel Limiting Law
To determine the activity coefficient (aC) of an ion C in a solution, we need to know two things: the concentration of the ion and its activity coefficient (γ).
The formula to find the activity coefficient is: aC = γ [C] / [C⊖], where:
- γ is the activity coefficient of ion C,
- [C⊖] represents the concentration under specific standard conditions (e.g., 1 mol/kg if using molality),
- [C] is the actual concentration of ion C.
When you divide [C] by [C⊖], you get a number without units.
To calculate the activity coefficient of an ion in a dilute solution with known ionic strength, we use the Debye–Hückel limiting law, which is expressed as:
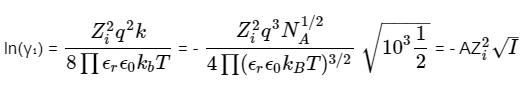
Here are the explanations for the variables:
- zi is the charge of ion species i,
- q is the charge of an electron,
- κ is the inverse of the Debye screening length (λ_D),
- εr is the relative permittivity of the solvent,
- ε0 is the permittivity of free space,
- kB is the Boltzmann constant,
- T is the temperature of the solution,
- NA is the Avogadro constant,
- I is the ionic strength of the solution, and
- A is a constant that varies with temperature.
In simpler terms, this equation helps us calculate the activity coefficient of ions in a solution with low ion concentration and known ionic strength, considering various factors like charge and temperature.
Main Assumptions of Debye Huckel Theory
- The solute or electrolyte is entirely separated, which means it’s a strong electrolyte.
- Ions are shaped like spheres, and this theory doesn’t consider how ions are surrounded by solvent.
- In this theory, the solvent doesn’t have a role; it’s just a place for interactions to happen.
- To explain, think of individual ions around a central ion as a cloudy area of charge.
So, there’s a sort of cloudy sphere around the central ion with a charge that’s equal in amount but opposite in sign. This is called its ionic atmosphere. The energy and chemical potential of the central ion are lowered because of its electric interaction with this ionic atmosphere
FAQs on Debye Huckel Theory
What is the Debye-Hückel equation?
The Debye-Hückel equation is a mathematical formula created to help us understand how things called ions behave in certain kinds of solutions, where ions are like tiny charged particles.
What are the principles of the Debye Huckel theory?
The Debye-Hückel theory relies on three ideas about how ions behave in a liquid: Electrolytes break apart into ions in the liquid. The liquid containing Electrolytes is very weak, around 0.01 M. Each ion is typically surrounded by ions of the opposite charge.
What is the D by Hückel limiting law?
The Debye-Hückel Limiting Law (DHLL) accurately describes the thermodynamic properties of weak electrolyte solutions. Many resources present this law by using Peter Debye and Erich Hückel's initial approach, which involves simplifying the Poisson-Boltzmann equation for a basic electrolyte model.
Give the Significance of the Debye Onsager Equation?
This equation explains how conductivity, a specific measurement, can help us understand the speed at which reactions happen in electrolyte solutions. It can also be used to figure out the strength of weak electrolytes (according to the Debye Huckel theory, which is focused on strong electrolytes). This depends on various factors, like how concentrated the electrolytes are in the solution. We typically use this theory when things in the solution aren't behaving ideally.






