Table of Contents
Diagonal of a Cube Formula
Introduction
The diagonal of a cube formula helps in calculating the lengths of the different diagonals of a cube – the face diagonals of cube and the body diagonals of cube. A cube is a three-dimensional solid figure, also known as a square solid, that has all edges of the same measure. This means that the length, width, and height of a cube are of equal measure, and each of its faces is a square. Let us learn more about the diagonal of a cube and the diagonal of a cube formula for measuring the lengths of the face diagonal and the body diagonals with examples.
What is the Diagonal of a Cube?
Face Diagonal of Cube: A face diagonal of a cube refers to a line segment connecting two vertices that lie on different faces of the cube. It runs through the interior of the cube, intersecting the edges and passing through the center of the cube.
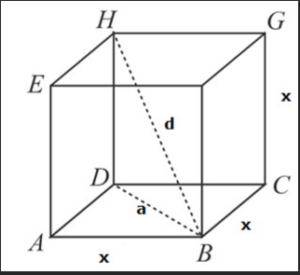
The formula to calculate the face diagonal of a cube can be derived using the Pythagorean theorem. In a cube, all sides are equal in length, denoted by “s”. Let “d” represent the length of the diagonal of cube.
By considering a right triangle formed by one side, the diagonal, and a face diagonal, we can apply the Pythagorean theorem:
s2+ s2 = a2
Simplifying the equation:
2s2 = a2
Taking the square root of both sides:
√(2s2) = √(a2)
√2s = a
Therefore, the formula for the diagonal of a cube is:
d = √2s
This formula allows for the direct calculation of the face diagonal length using the side length of the cube. It is helpful in various geometric and spatial calculations involving cubes, such as determining distances or sizes within a cube-based structure or object.
Body Diagonal of cube: The body diagonal of a cube refers to a line segment that connects two non-adjacent vertices of the cube. It can be visualized as a line passing through the cube’s interior, intersecting the opposite corners.
To calculate the length of the body diagonal of a cube, we can also use the Pythagorean theorem. Let “s” represent the length of the cube’s side, and “d” represent the length of the body diagonal of cube.
In a cube, the body diagonal forms a right triangle with three sides of length “s”. Applying the Pythagorean theorem, we have:
s2 + s2 + s2 = d2
Simplifying the equation:
3s2 = d2
Taking the square root of both sides, we get:
√(3s2) = √(d2)
√3s = d
Thus, the formula for the body diagonal of a cube is:
d = √3s
This formula allows us to find the length of the body diagonal using the side length of the cube. It is a valuable tool in various applications, including architecture, engineering, and three-dimensional geometry, where understanding the spatial relationships and measurements of cubes is necessary.
Solved Examples on Diagonal of Cube Formula:
Example 1: Find the length of the face diagonal and the body diagonal of a cube with a side length of 5 cm.
Solution:
The length of the face diagonal can be found using the formula: face diagonal (d) = side length (s).
Therefore, the face diagonal is 5 cm.
To find the length of the body diagonal, we use the formula: body diagonal (d) = √3s, where s is the side length.
Plugging in the value, we get:
body diagonal (d) = √3 x 5 cm = √75 cm ≈ 8.66 cm.
So, the length of the face diagonal is 5 cm, and the length of the body diagonal is approximately 8.66 cm.
Example 2: The body diagonal of a cube is 10 meters. What is the length of its side?
Solution:
Using the formula for the body diagonal, we have:
10 meters = √3s
Squaring both sides, we get:
100 = 3s2
Dividing by 3, we have:
33.33 = s2
Taking the square root, we find:
s ≈ 5.77 meters.
Hence, the length of the side of the cube is approximately 5.77 meters.
Related Links:
Volume of Parallelepiped Formula
Frequently Asked Questions on Diagonal of Cube formula
What is the formula for the diagonal of a cube?
The formula for the diagonal (d) of a cube is given by d = s√3, where s represents the side length of the cube. This formula allows us to calculate the length of the diagonal when the side length is known, or vice versa.
How many total diagonals are there in a cube?
In a cube, there are a total of four face diagonals. A face diagonal connects two vertices that lie on different faces of the cube. Each face diagonal extends along the surface of the cube, connecting two adjacent corners of different faces. In a cube, there are a total of four body diagonals. These diagonals are referred to as the body diagonals as they connect opposite vertices of the cube and pass through its interior. Each body diagonal extends through the three-dimensional space of the cube, forming line segments that intersect at the center of the cube. Therefore we can say that there are total 4 + 6 = 10 diagonals.
What is the relationship between diagonal of cube and volume?
The relationship between the diagonal of a cube and its volume can be determined using the Pythagorean theorem and the formula for the volume of a cube. Let's denote the side length of the cube as s and the length of the diagonal as d. The body diagonal is the longest diagonal in the cube, and it passes through the center of the cube. Using the Pythagorean theorem, we can establish the following relationship: s2 + s2 + s2 = d2 √3s = d To find the relationship between the diagonal and the volume, we can use the formula for the volume of a cube: V = s3 By substituting the value of s from the relationship above, we get: This equation shows that the volume of a cube is related to the diagonal by a power of 3/2.
What are the different types of diagonals in a cube?
Face Diagonal: A cube has 6 square-shaped faces. There are 2 diagonals on each face joining the non-adjacent vertices. Hence, there are 12 face diagonals in a cube. The length of the face diagonal can be calculated using the formula: body diagonal (d) = √2s, where s is the side length of the cube. Body Diagonal: The body diagonal connects two opposite vertices of the cube, passing through its interior. It is the longest diagonal in the cube and provides important spatial information. The length of the body diagonal can be calculated using the formula: body diagonal (d) = √3s, where s is the side length of the cube.
What is the difference between the face diagonal and the body diagonal of a cube?
The face diagonal connects two vertices that lie on different faces of the cube, while the body diagonal connects two opposite vertices of the cube, passing through its interior. The face diagonal is equal in length to the side length of the cube, whereas the body diagonal is longer and can be calculated using the formula: body diagonal (d) = √3s, where s is the side length.
How many diagonals are there in a cube?
There are two kinds of diagonals in a cube because it is a three-dimensional figure. A cube has 6 square-shaped faces. There are 2 diagonals on each face joining the non-adjacent vertices. Hence, there are 12 face diagonals in a cube. The body diagonals connect the opposite vertices of the cube passing through the body of the cube.
What is the Body Diagonal of a Cube?
Since a cube is a three-dimensional figure, there are 4 body diagonals in a cube. A body diagonal is also known as the 'space diagonal' or the 'solid diagonal' of a cube. The body diagonals connect the opposite vertices of the cube passing through the body of the cube. Hence, there are 4 body diagonals in a cube that pass through the cube connecting the opposite corners.
What is the Formula to Calculate the Diagonal of a Cube?
The formula to calculate the length of the body diagonal or the main diagonal of a cube is given as, Length of body diagonal of a cube = √3a, where a = Length of each side of a cube.







