Table of Contents
The Fibonacci Sequence is a series of numbers that begins with 0 and 1. Each number that follows in this series is the sum of the two numbers before it. The sequence starts like this: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, and continues indefinitely. In this article, we will discuss the Fibonacci Sequence in more detail.
Also Check: Vertices, Faces and Edges
Fibonacci Sequence Meaning
The Fibonacci sequence is defined as a unique series of numbers that starts with 0 and 1. In these sequences, each following number is the sum of the two preceding ones. The Fibonacci sequence is like: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, and so on. Each number in this series is referred to as a Fibonacci number, and the first two terms are 0 and 1. The below given formula can define the Fibonacci sequence:
Fn = Fn-1 + Fn-2 for every n>1
Also Check: Area of a Circle
Fibonacci Sequence List
As we know the Fibonacci sequence is defined by the below-mentioned formula:
Fn = Fn-1 + Fn-2 for every n>1
Therefore, the list of the first 20 terms of the Fibonacci sequence is discussed below:
F0 = 0
F1 = 1
F2 = 1
F3 = 2
F4 = 3
F5 = 5
F6 = 8
F7 = 13
F8 = 21
F9 = 34
F10 = 55
F11 = 89
F12 = 144
F13 = 233
F14 = 377
F15 = 610
F16 = 987
F17 = 1597
F18 = 2584
F19 = 4181
Also Check: CUBE
This sequence can be seen in the way each term is derived from the sum of the two terms before it, such that:
F2 = F1 + F0
F3 = F2 + F1
F4 = F3 + F2
And so on.
Fibonacci Sequence History
Fibonacci Sequence is named after Leonardo Fibonacci who was an Italian mathematician who introduced this sequence to the Western world in his book Liber Abaci in 1202. The Fibonacci Sequence has earned the nickname “nature’s secret code” due to its remarkable presence in the natural world.
Also Check: Average
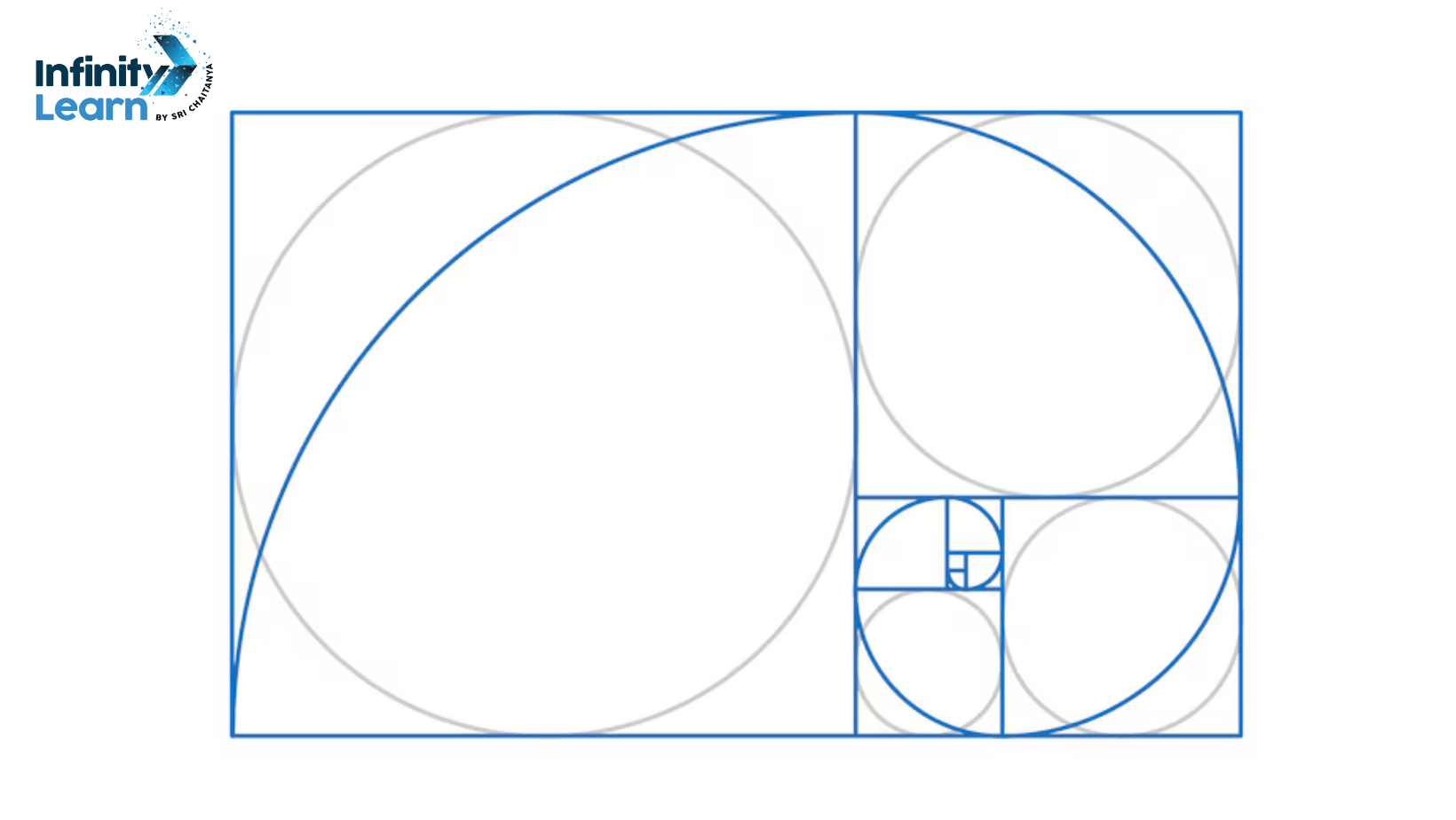
Fibonacci Sequence Spiral
The Fibonacci spiral is a geometric pattern that emerges from the Fibonacci sequence. It is constructed by drawing a series of connected quarter-circles within a sequence of squares. These squares are sized based on the numbers in the Fibonacci sequence, creating a visually appealing spiral that expands outward infinitely.
How to Draw a Fibonacci Sequence Spiral
- To create the Fibonacci spiral, you begin with a small square.
- Adjacent to it, you draw a larger square whose side length is the sum of the side lengths of the previous two squares.
- This process continues, with each new square having a side length equal to the sum of the side lengths of the last two squares.
- Inside each square, a quarter-circle is drawn, and these quarter-circles connect seamlessly, forming the spiral.
As the spiral grows, it closely approximates the golden ratio, which is approximately 1.618. The golden ratio is a special number that appears frequently in nature, art, and architecture, known for its special proportions. The Fibonacci spiral, therefore, not only serves as a beautiful mathematical pattern but also highlights the connection between mathematics and the natural world.
Also Check: Circumstance of Circle
Fibonacci Sequence Formula
The Fibonacci sequence, denoted as Fn is defined using a recursive formula,
Fn = Fn-1 + Fn-2 for every n>1
starting with the seed values 0 and 1, such that, F0 = 0 and F1 = 1.
This sequence is structured in two main parts:
Kick-off Part: This consists of the initial seed values that start the sequence:
F0 = 0 and F1 = 1
Recursive Relation: This defines how each subsequent term is calculated:
Fn = Fn-1 + Fn-2 for every n>1
It’s important to note that the sequence begins with 0, not 1. This means that the position of each term is crucial when discussing the sequence. For example, F5 is the 6th term in the sequence because the counting starts from F0. The sequence up to F5 looks like this:
| 1st term | F0 = 0 |
| 2nd term | F1 = 1 |
| 3rd term | F2 = 1 |
| 4th term | F3 = 2 |
| 5th term | F4 = 3 |
| 6th term | F5 = 5 |
Thus, the 6th term in the Fibonacci sequence is equal to 5. This recursive nature and careful indexing are what give the Fibonacci sequence its unique structure and properties, often seen in various natures.
Also Check: Acute Angle
Fibonacci Sequence Properties
Below discussed are the properties and patterns of the Fibonacci sequence:
1. Connection to the Golden Ratio
Fibonacci numbers are closely related to the golden ratio, denoted as where = 1.618034.
The Fibonacci number Fn can be approximated using the Binet formula:
Fn = ()n – (1 – )n 5
For example, to find F7
F7 = (1.618034)7 – (1 – 1.618034)7 5 13
This shows that as n increases, the Fibonacci number can be accurately predicted using the golden ratio.
2. Ratio of Successive Fibonacci Numbers
The ratio of successive Fibonacci numbers approaches the golden ratio as the numbers increase:
Fn + 1Fn 1.618034 as n
Here’s how the ratio evolves with increasing Fibonacci numbers:
| A | B | A/B |
| 2 | 3 | 1.5 |
| 3 | 5 | 1.6 |
| 5 | 8 | 1.6 |
| 8 | 13 | 1.625 |
| 144 | 233 | 1.618055555.. |
| 233 | 377 | 1.618025751… |
By multiplying a Fibonacci number by the golden ratio, you get an approximation of the next number in the sequence. For instance:
13 1.618034 21.034442
This result is close to 21, which is indeed the next Fibonacci number after 13.
3. Patterns in Multiples
The Fibonacci sequence also exhibits patterns related to multiples:
- Every 3rd number in the sequence (starting from 2) is a multiple of 2.
- Every 4th number (starting from 3) is a multiple of 3.
- Every 5th number (starting from 5) is a multiple of 5.
These patterns continue for larger numbers as well, illustrating the sequence’s inherent mathematical symmetry.
4. Fibonacci Sequence Below Zero
The Fibonacci sequence extends into negative indices using the formula:
F-n = (-1)n+1 Fn
For example:
F-4 = (-1)5 F4 = -1 3 = -3
This property shows that the Fibonacci sequence is symmetric around zero, with negative indices producing a mirrored sequence.
5. Sum of Fibonacci Numbers
The sum of the first n terms of the Fibonacci sequence can be calculated as:
i=0n Fi = Fn+2 – 1
For example, the sum of the first 10 terms is:
i=09 Fi = F12 – 1 = 89 – 1 = 88
This formula provides a quick way to sum up the terms of the sequence.
6. Connections to Other Mathematical Concepts
The Fibonacci sequence also links to other mathematical constructs:
- Lucas Numbers: It is similar to Fibonacci numbers but with different starting values.
- Pascal’s Triangle: Fibonacci numbers can be found in the sums of the diagonals of Pascal’s Triangle.
Fibonacci Sequence in Real Life
One can find the Fibonacci sequence in the spiral arrangements of sunflower seeds. More such examples of the Fibonacci Sequence in Real Life include the petals of daisies and the structure of broccoli and cauliflower. Even the intricate curves of seashells follow this numerical pattern of the Fibonacci Sequence.
Fibonacci Sequence: FAQs
What is the Fibonacci Sequence?
The Fibonacci sequence is a series of numbers where each term is the sum of the two preceding ones. It begins with 0 and 1 and continues infinitely as 0, 1, 1, 2, 3, 5, 8, 13, and so on.
Why is the Fibonacci Sequence Significant?
The Fibonacci sequence is significant because the ratio of two successive Fibonacci numbers approximates the golden ratio, which is approximately 1.618034. This ratio appears frequently in nature, art, and architecture, representing a pattern of growth and harmony.
What Are the First 10 Fibonacci Numbers?
The first 10 numbers in the Fibonacci sequence are 0, 1, 1, 2, 3, 5, 8, 13, 21, 34.
What Is the Value of the Golden Ratio?
The value of the golden ratio is approximately 1.618034.








