NCERT Solutions For Class 6 Maths Practical Geometry Exercise 14.5
NCERT Solutions For Class 6 Maths Chapter 14 Practical Geometry Ex 14.5
Exercise 14.5
Ex 14.5 Class 6 Maths Question 1.
Draw AB of length 7.3 cm and find its axis of symmetry.
Solution:
Step I: Draw \(\overline { AB }\) = 7.3 cm
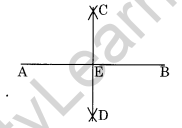
Step II: Taking A and B as centre and radius more than half of \(\overline { AB }\), draw two arcs which intersect each other at C and D.
Step III: Join C and D to intersect \(\overline { AB }\) at E. Thus, CD is the perpendicular bisector or axis of symmetry of \(\overline { AB }\).
Ex 14.5 Class 6 Maths Question 2.
Draw a line segment of length 9.5 cm and construct its perpendicular bisector.
Solution:
Step I: Draw a line segment \(\overline { PQ }\) =9.5 cm
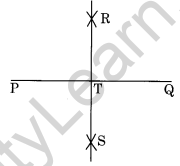
Step II: With centres P and Q and radius more than half of PQ, draw two arcs which meet each other at R and S.
Step III: Join R and S to meet \(\overline { PQ }\) at T.
Thus, RS is the perpendicular bisector of PQ.
Ex 14.5 Class 6 Maths Question 3.
Draw the perpendicular bisector of \(\overline { XY }\) whose length is 10.3 cm.
(a) Take any point P on the bisector drawn. Examine whether PX = PY.
(b) If M is the midpoint of \(\overline { XY }\) . What can you say about the length of MX and MY?
Solution:
Step I: Draw a line segment \(\overline { XY }\) = 10.3 cm.
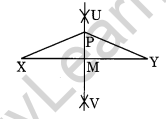
Step II : With centre X and Y and radius more than half of XY, draw two arcs which meet each other at U and V.
Step III: Join U and V which meets \(\overline { XY }\) at M.
Step IV: Take a point P on \(\overline { UV }\) .
(a) On measuring, PX = PY = 5.6 cm.
(b) On measuring, \(\overline { MX }\) = \(\overline { MY }\) = \(\frac { 1 }{ 2 }\) XY = 5.15 cm.
Ex 14.5 Class 6 Maths Question 4.
Draw a line segment of length 12.8 cm. Using compasses, divide it into four equal parts. Verify by actual measurement.
Solution:
Step I: Draw a line segment \(\overline { AB }\) = 12.8 cm
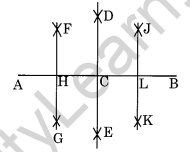
Step II : With centre A and B and radius more than half of AB, draw two arcs which meet each other at D and E.
Step III : Join D and E which meets \(\overline { AB }\) at C which is the midpoint of \(\overline { AB }\).
Step IV : With centre A and C and radius more than half of AC, draw two arcs which meet each other at F and G.
Step V: Join F and G which meets \(\overline { AC }\) at H which is the midpoint of \(\overline { AC }\) .
Step VI : With centre C and B and radius more than half of CB, draw two arcs which meet each other at J and K.
Step VII : Join J and K which meets \(\overline { CB }\) at L which is the midpoint of \(\overline { CB }\) .
Thus, on measuring, we find
\(\overline { AH }\) = \(\overline { HC }\) = \(\overline { CL }\) = \(\overline { LB }\) = 3.2 cm.
Ex 14.5 Class 6 Maths Question 5.
With \(\overline { PQ }\) of length 6.1 cm as diameter, draw a circle.
Solution:
Step I: Draw \(\overline { PQ }\) = 6.1 cm
Step II: Draw a perpendicular bisector of \(\overline { PQ }\) which meets \(\overline { PQ }\) at R i.e. R is the midpoint of \(\overline { PQ }\).
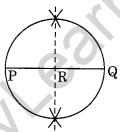
Step III : With centre R and radius equal to \(\overline { RP }\) , draw a circle passing through P and Q.
Thus, the circle with diameter \(\overline { PQ }\) = 6.1 cm is the required circle.
Ex 14.5 Class 6 Maths Question 6.
Draw a circle with centre C and radius 3.4 cm. Draw any chord \(\overline { AB }\) . Construct the perpendicular bisector of \(\overline { AB }\) and examine if it passes through C.
Solution:
Step I: Draw a circle with centre C and radius 3.4 cm.
Step II: Draw any chord \(\overline { AB }\).
Step III : Draw the perpendicular bisector of \(\overline { AB }\) which passes through the centre C.
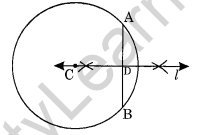
Ex 14.5 Class 6 Maths Question 7.
Repeat Question number 6, if \(\overline { AB }\) happens to be a diameter.
Solution:
Step I: Draw a circle with centre C and radius 3.4 cm.
Step II : Draw a diameter AB of the circle.
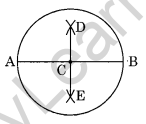
Step III : Draw a perpendicular bisector of AB which passes through the centre C and on measuring, we find that C is the midpoint of \(\overline { AB }\) .
Ex 14.5 Class 6 Maths Question 8.
Draw a circle of radius 4 cm. Draw any two of its chords. Construct the perpendicular bisectors of these chords. Where do they meet?
Solution:
Step I: Draw a circle with centre 0 and radius 4 cm.
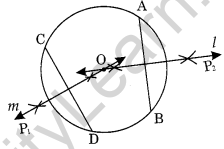
Step II: Draw any two chords \(\overline { AB }\) and \(\overline { CD }\) of the circle.
Step III : Draw the perpendicular bisectors of \(\overline { AB }\) and \(\overline { CD }\) i.e. I and m.
Step IV : On producing the two perpendicular bisectors meet each other at the centre O of the circle.
Ex 14.5 Class 6 Maths Question 9.
Draw any angle with vertex O. Take a point A on one of its arms and B on another such that OA = OB. Draw the perpendicular bisectors of \(\overline { OA }\) and \(\overline { OB }\) . Let them meet at P. Is PA = PB?
Solution:
Step I: Draw an angle XOY with O as its vertex.
Step II : Take any point A on OY and B on OX, such that OA + OB.
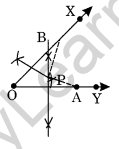
Step III : Draw the perpendicular bisectors of OA and OB which meet each other at a point P.
Step IV : Measure the lengths of \(\overline { PA }\) and \(\overline { PB }\). Yes, \(\overline { PA }\) = \(\overline { PB }\).




