Class 12 Maths Chapter 4 Determinants MCQs are designed to assist students in scoring well in the CBSE board exam 2023-24. These multiple-choice questions align with the new CBSE guidelines for the academic year 2023-24, covering all topics and subtopics of Chapter 4 Determinants from the NCERT textbook. Practicing these MCQs will help students prepare effectively for their exams. Access all Class 12 Maths MCQs for every chapter at Infinitylearn.com.
Determinants Class 12 Maths MCQs Pdf
Question 1.
Answer: B
Question 2.
Answer: B
Question 3. If A is a square matrix of order 3 and |A| = 5, then the value of |2A′| is
(a) -10
(b) 10
(c) -40
(d) 40
Answer: D
Question 4. Find the value of x for which the matrix
(a) 0, 1
(b) 1, 3
(c) 0, 3
(d) 3, 2
Answer: C
Question 5.
Answer: B
Question 6. The area of a triangle with vertices (-3, 0), (3, 0) and (0, k) is 9 sq. units. The value of k will be
(a) 9
(b) 3
(c) -9
(d) 6
Answer: (b)
Question 7. The area of a triangle with vertices (–3, 0), (3, 0) and (0, k) is 9 sq. units. The value of k will be
(a) 9
(b) 3
(c) -9
(d) 6
Answer: (b)
Latest: CBSE Class 12 Maths Answer Key 2024 | CBSE Class 12 Maths Paper Analysis 2024
Question 8.
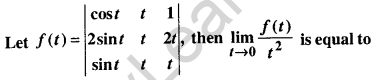
(a) 0
(b) -1
(c) 2
(d) 3
Answer: (a)
Question 9.
Answer: A
Question 10. Given that A is a square matrix of order 3 and |A| = -4, then |adj A| is equal to
(a) -4
(b) 4
(c) -16
(d) 16
Answer: D
Question 11. Which of the following is correct?
(a) Determinant is a square matrix.
(b) Determinant is a number associated with a matrix.
(c) Determinant is a number associated with a square matrix.
(d) None of these
Answer: C
Question 12. Compute (AB)-1, If
Answer: A
Question 13.
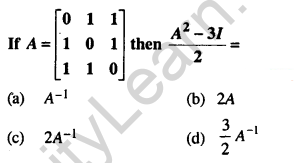
Answer: A
Question 14.
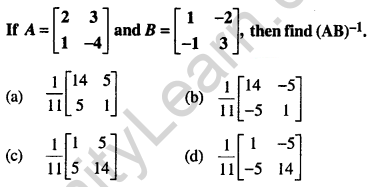
Answer: (a)
Question 15.
Answer: (b)
Question 16. If the points (3, -2), (x, 2), (8, 8) are collinear, then find the value of x.
(a) 2
(b) 3
(c) 4
(d) 5
Answer: (d) 5
Question 17. Using determinants, find the equation of the line joining the points (1, 2) and (3, 6).
(a) y = 2x
(b) x = 3y
(c) y = x
(d) 4x – y = 5
Answer: (a)
Question 18. If A is an invertible matrix of order 2, then det (A–1) is equal to
(a) det (A)
(b) 1/det (A)
(c) 1
(d) 0
Answer: B
Question 19.
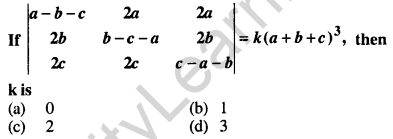
Answer: (b)
Question 20.
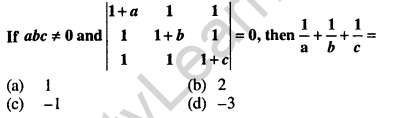
Answer: (c)
Question 21.
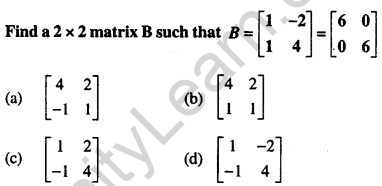
Answer: A
Question 22. If for the non-singular matrix A, A2 = I, then find A-1.
(a) A
(b) I
(c) O
(d) None of these
Answer: A
Question 23. If the equation a(y + z) = x, b(z + x) = y, c(x + y) = z have non-trivial solutions then the value of \(\frac{1}{1+a}+\frac{1}{1+b}+\frac{1}{1+c}\) is
(a) 1
(b) 2
(c) -1
(d) -2
Answer: (b)
Question 24. A non-trivial solution of the system of equations x + λy + 2z = 0, 2x + λz = 0, 2λx – 2y + 3z = 0 is given by x : y : z =
(a) 1 : 2 : -2
(b) 1 : -2 : 2
(c) 2 : 1 : 2
(d) 2 : 1 : -2
Answer: (d)
Question 25. If 4x + 3y + 6z = 25, x + 5y + 7z = 13, 2x + 9y + z = 1, then z = ________
(a) 1
(b) 3
(c) -2
(d) 2
Answer: (d)
Question 26. If the equations 2x + 3y + z = 0, 3x + y – 2z = 0 and ax + 2y – bz = 0 has non-trivial solution, then
(a) a – b = 2
(b) a + b + 1 = 0
(c) a + b = 3
(d) a – b – 8 = 0
Answer: (a)
Question 27. Solve the following system of equations x – y + z = 4, x – 2y + 2z = 9 and 2x + y + 3z = 1.
(a) x = -4, y = -3, z = 2
(b) x = -1, y = -3, z = 2
(c) x = 2, y = 4, z = 6
(d) x = 3, y = 6, z = 9
Answer: (b)
Question 28. If the system of equations x + ky – z = 0, 3x – ky – z = 0 & x – 3y + z = 0 has non-zero solution, then k is equal to
(a) -1
(b) 0
(c) 1
(d) 2
Answer: (c)
Question 29. Find the area of the triangle with vertices P(4, 5), Q(4, -2) and R(-6, 2).
(a) 21 sq. units
(b) 35 sq. units
(c) 30 sq. units
(d) 40 sq. units
Answer: (b)
Question 30. If the points (a1, b1), (a2, b2) and(a1 + a2, b1 + b2) are collinear, then
(a) a1b2 = a2b1
(b) a1 + a2 = b1 + b2
(c) a2b2 = a1b1
(d) a1 + b1 = a2 + b2
Answer: (a)
Also Read: CBSE Class 12 Maths Syllabus
Question 31. If the points (2, -3), (k, -1) and (0, 4) are collinear, then find the value of 4k.
(a) 4
(b) 7/140
(c) 47
(d) 40/7
Answer: (d)
Question 32. Find the area of the triangle whose vertices are (-2, 6), (3, -6) and (1, 5).
(a) 30 sq. units
(b) 35 sq. units
(c) 40 sq. units
(d) 15.5 sq. units
Answer: (d)
