Derivatives

Introduction to Derivatives

Derivatives are important tools in calculus that are used to examine the rate of change and slope of functions. They quantify how functions act locally, revealing information about critical points, optimisation, and curve behaviour. Derivatives are important in many scientific areas, including physics, engineering, economics, and many more.

Meaning of Derivative

A derivative in mathematics represents the rate of change of a function at any given position. It measures how the function’s output value varies when its input variable changes. The derivative, which is often expressed as the slope of the function’s tangent line at a certain location, is an important concept in calculus.

Derivative in mathematics with examples:

In mathematics, derivatives are used to calculate the rate at which a function changes in relation to its input variable. Here are a couple such examples:

Think about the function f(x) = x². The power rule is used to determine the derivative of this function, represented as f(x) = d/dx(f(x)) = 2x f'(x) in this example. This derivative informs us that every unit increase in raises the function’s output by 2x.

As an example, consider the function g(x) = sinx Its derivative, g'(x) = d/dx(g(x)) = cosx, may be determined using the trigonometric function derivative. g'(x) = cosx in this example. This derivative indicates that the cosine function represents the sine function’s rate of change..

Steps to find the derivative:

Certainly! In mathematics, you may find the derivative of a function by following these general steps:

• Determine the function: Assume you have a function, such as f(x).
• Define the derivative: A function’s derivative indicates its rate of change at any given moment. It describes the behaviour of the function as you travel along the x-axis.
• Use the derived definition: A function’s derivative f(x) can be defined as the limit of the difference quotient as the change in x (denoted as x) approaches zero. This is stated mathematically as:
• This equation describes the slope of the function’s tangent line at a certain location (x).
• Simplify the formula by replacingwith its equivalent expression in terms of x. The numerator should be expanded and simplified.
• Consider this: As approaches 0, calculate the limit. This will tell you the function’s derivative at the point x.
• When you have evaluated the limit, you will get the derivative of the function at the specified point. Depending on the notation method you want, you may write it as f'(x) or dy/dx.

To obtain derivatives for different types of functions, multiple differentiation rules and approaches are available, such as the power rule, product rule, chain rule, and so on. These guidelines give shortcuts and help make the process of locating derivatives easier. The techniques detailed above, on the other hand, give a generic strategy for obtaining derivatives using the specification.

Formulas in derivatives

First principle of derivative is

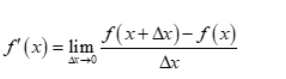
Derivatives of algebraic functions

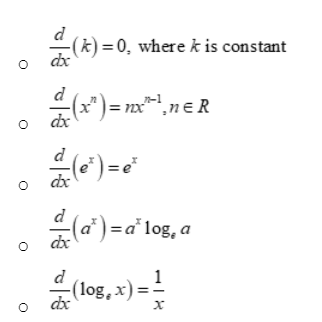
Derivatives of trigonometric functions

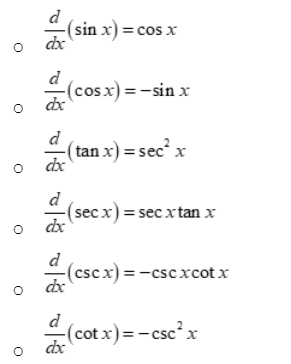
Derivatives of inverse trigonometric functions

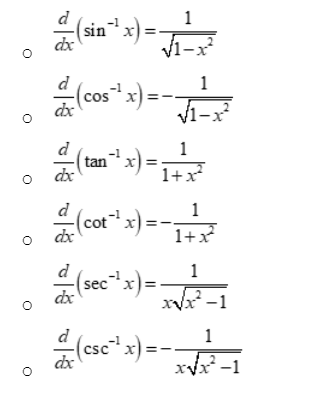
Derivatives of hyperbolic functions

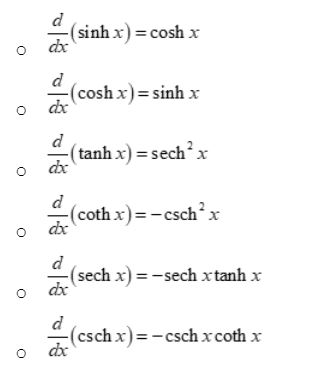
Derivatives of inverse hyperbolic functions

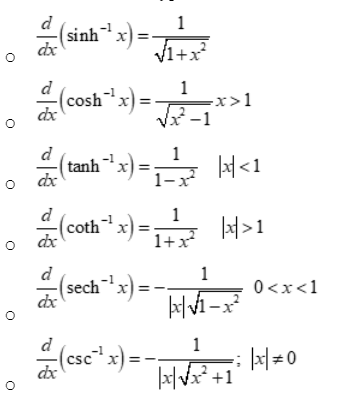
Methods of derivatives

The rate of change of a function with respect to its independent variable is referred to as its derivative in mathematics. Different forms of derivatives are often employed in mathematical analysis. Here are a few examples:

• Ordinary differentiation
• Partial differentiation
• Implicit differentiation
• Logarithmic differentiation
• Higher order derivatives

Math Articles Math Formulas Integral Formulas Differentiation Formulas

Key Concepts on Derivatives

• Derivatives are an important subject in mathematics, especially in calculus. They give useful information on the rate of change of functions and aid in the analysis of mathematical models’ behaviour. Here are some fundamental principles in mathematics linked to derivatives:
• Derivatives quantify the rate at which a function varies in relation to its independent variable. They describe how the output of a function responds to changes in its input. The derivative at a given point reflects the rate of change at that moment in time.
• Tangent Line: The slope of the tangent line to the graph of a function at a particular point is represented by the derivative of that function at that location. The tangent line is a straight line that has the same slope as the derivative and intersects the curve of the function at that point.
• Differentiability is defined as the existence of a derivative for every point in a function’s domain. Differentiability implies smoothness and shows that the function’s tangent lines may be used to approximate it well.
• The chain rule is a fundamental rule for determining the derivative of a function composition. It asserts that if a function is made up of two or more functions, the derivative may be calculated by multiplying the derivatives of the individual functions and applying the relevant chain rule formula.
• Implicit Differentiation: Implicit differentiation is a technique for determining the derivative of a function that is implicitly specified by an equation. It entails separating both sides of the equation in terms of the independent variable and considering the dependent variable as a function of the independent variable.
• Derivatives play an important part in optimisation situations when the objective is to find the greatest or lowest values of a function. We can identify possible maxima and minima by analysing the derivative and determining crucial locations where the derivative is zero or does not exist.
• Related Rates: Related rate questions entail employing derivatives to determine the rate at which one quantity changes in relation to another. These issues frequently entail using the chain rule to determine the link between the rates of change of several variables.
• Derivative Rules: There are various derivative rules that might help you locate derivatives faster. The power rule, product rule, quotient rule, and chain rule are examples of these. Understanding and using these criteria helps improve the efficiency with which derivatives are computed.

In mathematics, derivatives are a powerful tool that allows us to analyse functions, solve optimisation issues, represent physical processes, and investigate the behaviour of mathematical objects. They are widely utilised in a variety of domains including as physics, engineering, economics, and computer science.

Properties of derivatives

The properties of the derivative of a function in mathematics are as follows:

• Constant Rule: The derivative of a constant is zero. If f(x) = c (where c is a constant), then f'(x) = 0.
• Power Rule: The derivative of x^n is nx^(n-1). If f(x) = x^n, then f'(x) = nx^(n-1).
• Sum/Difference Rule: The derivative of a sum or difference of functions is the sum or difference of their derivatives. If f(x) = u(x) + v(x), then f'(x) = u'(x) + v'(x).
• Product Rule: The derivative of a product of functions is given by (uv)’ = u’v + uv’. If f(x) = u(x) * v(x), then f'(x) = u'(x) * v(x) + u(x) * v'(x).
• Quotient Rule: The derivative of a quotient of functions is given by (u/v)’ = (u’v – uv’) / v^2. If f(x) = u(x) / v(x), then f'(x) = (u'(x) * v(x) – u(x) * v'(x)) / v^2(x).
• Chain Rule: The derivative of a composite function (f(g(x))) is given by f'(g(x)) * g'(x). If f(u) and g(x) are differentiable, then the derivative of f(g(x)) with respect to x is f'(g(x)) * g'(x).
• Inverse Function Rule: If f(x) and g(x) are inverses of each other, then (g(f(x)))’ = 1 / f'(g(x)). In other words, the derivative of the inverse function is the reciprocal of the derivative of the original function.
• Derivative of Exponential Functions: The derivative of e^x (where e is Euler’s number) is e^x. For other exponential functions, the derivative is the function itself multiplied by the natural logarithm of the base.
• Derivative of Trigonometric Functions: The derivatives of trigonometric functions like sin(x), cos(x), tan(x), etc., have specific rules based on their trigonometric identities.

These properties are essential for calculating derivatives of functions and are the foundation of differential calculus, which deals with rates of change and slopes of curves.

Frequently asked questions on Derivatives

What is derivative in Maths?

A derivative measures the rate of change of a function with respect to its input variable. It represents the slope of the tangent line to the function's curve at a point.

What is the derivative formula?

The derivative formula is f'(x) = lim h->0 (f(x + h) - f(x))/h. It gives the derivative of f(x) by calculating the slope of secant lines approaching the tangent line.

What are the 7 rules of derivatives?

These are the 7 rules of derivatives:
1) Constant Rule
2) Power Rule
3) Constant Multiple Rule
4) Sum Rule
5) Difference Rule
6) Product Rule
7) Quotient Rule

How do you explain derivatives simply calculus?

Derivatives show how a function's output changes compared to small changes in the input. They measure the rate of change of one variable compared to another.

What is the concept of derivative?

The derivative concept shows how fast a function's value is changing with respect to its variable. It captures the function's sensitivity to change.

What is the formula for derivative?

The derivative formula relates the function's rate of change at a point to the slope of tangent line. It calculates the limit of difference quotients as they approach the tangent slope.