Table of Contents
What is Velocity?
Velocity is a fundamental concept in physics that describes the rate of change of an object’s position with respect to time. It is a vector quantity, meaning it has both magnitude and direction. Velocity is a key parameter for understanding the motion of objects and plays a significant role in various scientific and everyday applications. The velocity formula is v – d/t.
Velocity differs from speed, which only represents the magnitude of motion without considering direction. While speed tells us how fast an object is moving, velocity provides additional information by specifying both the speed and direction of motion. For example, if a car is traveling at a constant speed of 60 kilometers per hour, its velocity would be 60 kilometers per hour in a specific direction, such as east or west.
Formula of Velocity
The formula for velocity is:
𝑣 = 𝑑/𝑡
where:
- 𝑣 is the velocity
- 𝑑 is the displacement (the change in position)
- 𝑡 is the time taken for that displacement
Velocity is a vector quantity, which means it has both magnitude and direction. This distinguishes it from speed, which is a scalar quantity and only has magnitude.
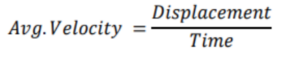
The displacement (Δx) represents the change in the position of an object, measured in a particular direction, while the time (Δt) refers to the interval during which the displacement occurred. Average velocity provides information about the overall change in position over a given time period.
Instantaneous velocity refers to the velocity of an object at a specific moment in time. It is determined by calculating the limit of the average velocity as the time interval approaches zero. Instantaneous velocity provides the precise velocity of an object at any given instant.
Velocity can be positive, negative, or zero, depending on the direction of motion. A positive velocity indicates motion in the positive direction, while a negative velocity represents motion in the opposite direction. Zero velocity signifies that the object is not changing its position.
Velocity is closely related to the concept of acceleration. Acceleration measures the rate of change of an object’s velocity with respect to time. If an object’s velocity changes, it means the object is experiencing acceleration. Acceleration can be positive (speeding up) or negative (slowing down), and it affects the object’s velocity accordingly.
Final Velocity Formula
formula for final velocity (vf ) depends on the context. There are several scenarios in which you might be calculating final velocity,
1. When initial velocity (vi), acceleration (a), and time (t) are known:
vf = vi + at
2. When initial velocity (vi), acceleration (a), and displacement (d) are known:v2f = v2i + 2ad
Then solve for vf:
vf = √(v2i + 2 ad)
3. In the context of free fall (ignoring air resistance) where the acceleration is due to gravity (g):
vf = vi + g t
Where g ≈ 9.81 m/s2 (on Earth).
Initial Velocity Formula
The formula for initial velocity depends on the context of the motion being described. Here are a common scenarios:
1. Uniformly Accelerated Motion (using equations of motion):
If you know the final velocity (v), acceleration (a), and time (t):
u = v – at
If you know the final velocity (v), acceleration (a), and displacement (s):
u = √(v2 – 2as)
2. From rest (initial velocity is zero):
If an object starts from rest, the initial velocity (u) is:
u = 0
3. Using average velocity:
If you know the average velocity (vavg), and initial and final velocities:
u = 2vavg – v
where vavg = (u + v) / 2.
What is the Unit of Velocity?
The established SI unit for Velocity is the same as that of speed. That is meters per second. However, velocity can also be expressed in other units depending on the context, such as kilometers per hour (km/h), miles per hour (mph), or feet per second (ft/s).
Solved Examples on Velocity Formula
Example 1: A car travels a distance of 200 kilometers in 4 hours. Calculate its average velocity.
Solution:
Given:
Distance (d) = 200 km
Time (t) = 4 hours
To calculate average velocity, we use the formula:
Average Velocity (v) = Displacement (Δx) / Time (Δt)
In this case, since the car traveled a straight distance without any change in direction, the displacement is equal to the distance covered. So, the displacement (Δx) is 200 km.
Substituting the values into the formula:
v = 200 km / 4 hours
v = 50 km/h
Therefore, the average velocity of the car is 50 kilometers per hour.
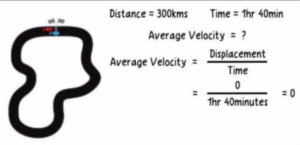
Example 2: Suppose a car driver finished a 300 km race in one hour and forty minutes on a racetrack having the start line and the finish line at the same point. What was the average velocity of that car?
Solution: The driver started the race and ended it at the same point. This means the displacement of the car is zero. And zero divided by the taken time, which is one hour forty minutes equals zero. That puts the average velocity for the race today at zero meters per second.
Example 3: A train travels a distance of 500 meters in 25 seconds. Calculate its velocity.
Solution:
Given:
Distance (d) = 500 meters
Time (t) = 25 seconds
To calculate velocity, we use the formula:
Velocity (v) = Distance (d) / Time (t)
Substituting the given values into the formula:
v = 500 meters / 25 seconds
v = 20 meters per second
Therefore, the velocity of the train is 20 meters per second.
Velocity Formula in Different Terms
Velocity Formula in Terms of Angular Velocity
If you know the angular velocity (ω) and radius (r):
v = ωr
Velocity Formula in Fluid Mechanics
Flow Rate and Velocity
The flow rate (Q) is related to the average velocity (v̄) and cross-sectional area (A) by:
Q = A * v̄
Velocity Formula in Terms of Acceleration
If you know the initial velocity (u), acceleration (a), and time (t):
v = u + at
Velocity Formula in Oscillation
If you know the amplitude (A), angular frequency (ω), and time (t):
v(t) = -Aωsin(ωt + ϕ) = –Vmax sin(ωt + ϕ)
where:
- v(t) represents the velocity of the oscillating particle at time 𝑡.
- A is the amplitude of the oscillation
- ω is the angular frequency of the oscillation
- ϕ is the phase angle
- Vmax is the maximum velocity of the oscillating particle, where Vmax = Aω = √A√ km
Velocity Formula in Circular Motion
The velocity formula in circular motion is given by:
vc = 2πr/T = ωr
where:
- vc = is the circular velocity
- r = is the radius of the circular path
- T = is the period (time for one revolution)
- ω = is the angular velocity in radians per second
FAQ’s on Velocity Formula
What is velocity?
Velocity is a vector quantity that represents the rate of change of an object's position with respect to time. It includes both the speed and direction of motion.
How is velocity different from speed?
While both velocity and speed describe how fast an object is moving, velocity also specifies the direction of motion, whereas speed does not consider direction.
What is the SI unit of velocity?
The SI unit of velocity is meters per second (m/s).
How is average velocity calculated?
Average velocity is determined by dividing the displacement of an object by the time taken. The formula is: Average Velocity = Displacement / Time.
What is the difference between average velocity and instantaneous velocity?
Average velocity represents the overall change in position over a given time interval, while instantaneous velocity refers to the velocity of an object at a specific instant in time.
Can velocity be negative?
Yes, velocity can be positive, negative, or zero. A positive velocity indicates motion in one direction, a negative velocity represents motion in the opposite direction, and zero velocity means no motion.









