Table of Contents
CBSE Class 8 Maths Important Questions for Linear Equations in One Variable
The essential questions for Class 8 Maths, Chapter 2, focus on the fundamental concepts of linear equations in one variable. These questions are available for free download in PDF format from Infinity Learn, providing students with valuable practice resources for their class 8 examinations. Aligned with the CBSE Class 8 updated syllabus, these questions are designed with an examination perspective, making them an excellent tool for students’ exam preparation.
At Infinity Learn, you can access NCERT Solutions for all subjects and classes free of charge, including NCERT Solutions for Class 8 Science. These resources facilitate comprehensive CBSE syllabus revisions and assist students in scoring higher marks in their examinations.
Topics Covered in Chapter 2 – Linear Equations in One Variable
- Introduction to algebraic expressions and equations: This section introduces students to the basics of algebraic expressions and equations, setting the foundation for understanding linear equations in one variable.
- Solving equations with linear expressions on one side and numbers on the other side: Students learn to solve equations where linear expressions are on one side and numbers on the other, mastering essential problem-solving techniques.
- Some applications of linear equations: This section showcases practical applications of linear equations, helping students understand the relevance of these concepts in real-world scenarios.
- Solving equations having the variable on both sides: Students tackle equations containing variables on both sides, expanding their problem-solving skills and deepening their understanding of linear equations.
- Reducing equations to a simpler form: This section teaches students to simplify complex equations into a more manageable form, making problem-solving more accessible and efficient.
- Equations reducible to the linear form: Students learn to identify and reduce equations to their linear form, further enhancing their problem-solving abilities in linear equations.
By practicing these important questions, students can strengthen their understanding of linear equations in one variable and improve their exam performance.
Class 8 Maths Chapter 2 Extra Questions Very Short Answer Type
Question 1. Identify the algebraic linear equations from the given expressions.
(a) x2 + x = 2
(b) 3x + 5 = 11
(c) 5 + 7 = 12
(d) x + y2 = 3
Solution:
(a) x2 + x = 2 is not a linear equation.
(b) 3x + 5 = 11 is a linear equation.
(c) 5 + 7 = 12 is not a linear equation as it does not contain variable.
(d) x + y2 = 3 is not a linear equation.
Question 2. Check whether the linear equation 3x + 5 = 11 is true for x = 2.
Solution:
Given that 3x + 5 = 11
For x = 2, we get
LHS = 3 × 2 + 5 = 6 + 5 = 11
LHS = RHS = 11
Hence, the given equation is true for x = 2
Question 3. Form a linear equation from the given statement: ‘When 5 is added to twice a number, it gives 11.’
Solution:
As per the given statement we have
2x + 5 = 11 which is the required linear equation.
Question 4. If x = a, then which of the following is not always true for an integer k. (NCERT Exemplar)
(a) kx = ak
(b) \(\frac { x }{ k }\) = \(\frac { a }{ k }\)
(c) x – k = a – k
(d) x + k = a + k
Solution: Correct answer is (b).
Question 5. Solve the following linear equations:
(a) 4x + 5 = 9
(b) x + \(\frac { 3 }{ 2 }\) = 2x
Solution:
(a) We have 4x + 5 = 9
⇒ 4x = 9 – 5 (Transposing 5 to RHS)
⇒ 4x = 4
⇒ x = 1 (Transposing 4 to RHS)
(b) We have x + \(\frac { 3 }{ 2 }\) = 2x
⇒ \(\frac { 3 }{ 2 }\) = 2x – x
⇒ x = \(\frac { 3 }{ 2 }\)
Question 6. Solve the given equation 3\(\frac { 1 }{ x }\) × 5\(\frac { 1 }{ 4 }\) = 17\(\frac { 1 }{ 2 }\)
Solution:
We have 3\(\frac { 1 }{ x }\) × 5\(\frac { 1 }{ 4 }\) = 17\(\frac { 1 }{ 2 }\)

Question 7. Verify that x = 2 is the solution of the equation 4.4x – 3.8 = 5.
Solution:
We have 4.4x – 3.8 = 5
Putting x = 2, we have
4.4 × 2 – 3.8 = 5
⇒ 8.8 – 3.8 = 5
⇒ 5 = 5
L.H.S. = R.H.S.
Hence verified.
Question 8.
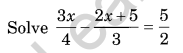
Solution:
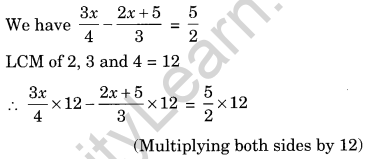
⇒ 3x × 3 – (2x + 5) × 4 = 5 × 6
⇒ 9x – 8x – 20 = 30 (Solving the bracket)
⇒ x – 20 = 30
⇒ x = 30 + 20 (Transposing 20 to RHS)
⇒ x = 50
Hence x = 50 is the required solution.
Question 9. The angles of a triangle are in the ratio 2 : 3 : 4. Find the angles of the triangle.
Solution:
Let the angles of a given triangle be 2x°, 3x° and 4x°.
2x + 3x + 4x = 180 (∵ Sum of the angles of a triangle is 180°)
⇒ 9x = 180
⇒ x = 20 (Transposing 9 to RHS)
Angles of the given triangles are
2 × 20 = 40°
3 × 20 = 60°
4 × 20 = 80°
| More Resources – NCERT Solutions for Class 8 | |
| NCERT Solutions for Class 8 Science | NCERT Solutions for Class 8 Social Science |
| NCERT Solutions for Class 8 English | NCERT Solutions for Class 8 Maths |
Question 10. The sum of two numbers is 11 and their difference is 5. Find the numbers.
Solution:
Let one of the two numbers be x.
Other number = 11 – x.
As per the conditions, we have
x – (11 – x) = 5
⇒ x – 11 + x = 5 (Solving the bracket)
⇒ 2x – 11 = 5
⇒ 2x = 5 + 11 (Transposing 11 to RHS)
⇒ 2x = 16
⇒ x = 8
Hence the required numbers are 8 and 11 – 8 = 3.
Question 11. If the sum of two consecutive numbers is 11, find the numbers.
Solution:
Let the two consecutive numbers be x and x + 1.
As per the conditions, we have
x + x + 1 = 11
⇒ 2x + 1 = 11
⇒ 2x = 11 – 1 (Transposing 1 to RHS)
⇒ 2x = 10
x = 5
Hence, the required numbers are 5 and 5 + 1 = 6.
Linear Equations in One Variable Class 8 Extra Questions Short Answer Type
Question 12. The breadth of a rectangular garden is \(\frac { 2 }{ 3 }\) of its length. If its perimeter is 40 m, find its dimensions.
Solution:
Let the length of the garden be x m
its breadth = \(\frac { 2 }{ 3 }\) × m.
Perimeter = 2 [length + breadth]

Question 13. The difference between two positive numbers is 40 and the ratio of these integers is 1 : 3. Find the integers.
Solution:
Let one integer be x.
Other integer = x – 40
As per the conditions, we have
\(\frac { x-40 }{ x }\) = \(\frac { 1 }{ 3 }\)
⇒ 3(x – 40) = x
⇒ 3x – 120 = x
⇒ 3x – x = 120
⇒ 2x = 120
⇒ x = 2
Hence the integers are 60 and 60 – 40 = 20.
Question 14. Solve for x:
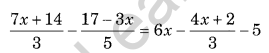
Solution:


Question 15. The sum of a two-digit number and the number obtained by reversing its digits is 121. Find the number if it’s unit place digit is 5.
Solution:
Unit place digit is given as 5
Let x be the tens place digit
Number formed = 5 + 10x
Number obtained by reversing the digits = 5 × 10 + x = 50 + x
As per the conditions, we have
5 + 10x + 50 + x = 121
⇒ 11x + 55 = 121
⇒ 11x = 121 – 55 (Transposing 55 to RHS)
⇒ 11x = 66
⇒ x = 6
Thus, the tens place digit = 6
Hence the required number = 5 + 6 × 10 = 5 + 60 = 65
Linear Equations in One Variable Class 8 Extra Questions Higher Order Thinking Skills (HOTS)
Question 16. If the length of the rectangle is increased by 40% and its breadth is decreased by 40%, what will be the percentage change in its perimeter?
Solution:
Let the length of the rectangle be x m and its breadth be y m
Perimeter = 2(x + y)
Now the length of the rectangle becomes after a 40% increase


Question 17. A fruit seller buys some oranges at the rate of ₹ 5 per orange. He also buys an equal number of bananas at the rate of ₹ 2 per banana. He makes a profit of 20% on oranges and a profit of 15% on bananas. In the end, he sold all the fruits. If he earned a profit of ₹ 390, find the number of oranges.
Solution:
Let the number of oranges bought by him be x and also the number of bananas be x.
Cost of x oranges at the rate of ₹ 5 per orange = ₹ 5x
Cost of x bananas at the rate of ₹ 2 per banana = ₹ 2x

Question 18. A steamer goes downstream from one point to another in 7 hours. It covers the same distance upstream in 8 hours. If the speed of stream be 2 km/h, find the speed of the steamer in still water and the distance between the ports. (NCERT Exemplar)
Solution:
Let speed of steamer in still water = x km/h
Speed of stream = 2 km/h
Speed downstream = (x + 2) km/h
Speed upstream = (x – 2) km/h
Distance covered in 7 hours while downstream = 7(x + 2)
Distance covered in 8 hours while upstream = 8(x – 2)
According to the condition,
7(x + 2) = 8(x – 2)
⇒ 7x + 14 = 8x – 16
⇒ x = 30 km/h
Total Distance = 7(x + 2) km = 7(30 + 2) km = 7 × 32 km = 224 km.



















![]()

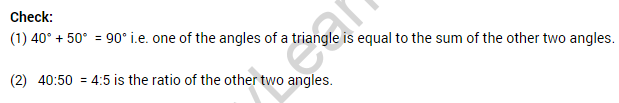









CBSE Class 8 Maths Class 2 Important Questions FAQs
What are the chapters covered in the important questions for CBSE Class 8 Maths?
The important questions for CBSE Class 8 Maths cover all 16 chapters, including Linear Equations in One Variable, Rational Numbers, Exponents and Powers, Algebraic Expressions and Identities, Square and Square Roots, Cube and Cube Roots, Comparing Quantities, Algebraic Expressions, Linear Equations in Two Variables, Understanding Quadrilaterals, Practical Geometry, Data Handling, and Mensuration.
Which type of questions of CBSE Class 8 Mathematics are easiest to score?
Questions based on basic concepts, direct formulas, and straightforward calculations are generally the easiest to score in CBSE Class 8 Mathematics. These questions are often found in the Exercises section of the NCERT textbook and are covered in the important questions provided by Infinity Learn.
Will practicing the important questions for CBSE Class 8 Mathematics help to improve my maths score?
es, practicing the important questions for CBSE Class 8 Mathematics can significantly improve your maths score. These questions are designed to cover the entire syllabus and are prepared by experts to help students understand and master key concepts.
What is the blueprint of the Class 8 Maths question paper?
The CBSE Class 8 Maths question paper typically consists of multiple-choice questions (MCQs), short-answer questions, and long-answer questions. The paper is divided into sections based on the chapters and topics, and the weightage of marks varies accordingly.
How to download chapter-wise PDF Solutions of Class 8 Maths?
To download chapter-wise PDF Solutions of Class 8 Maths, visit Infinity Learn's website and navigate to the resources section. Here, you can find free PDF downloads for all chapters, complete with detailed solutions prepared by experienced subject matter experts.
How to make a study plan for Class 8 Maths?
To make a study plan for Class 8 Maths, start by identifying the chapters and topics that require the most attention. Allocate sufficient time for each chapter, ensuring that you practice both theory and problem-solving questions. Regularly review your progress and adjust your study plan as needed.





